
“Prevention is better than cure,” goes the old saying, reminding us that it is easier to prevent something from happening in the first place than to repair the damage once it has occurred.
In the era of artificial intelligence (ai), this proverb underlines the importance of avoiding potential errors, such as overfitting, through techniques such as regularization.
In this article, we will discover regularization starting with its fundamental principles for its application using Sci-kit Learn (machine learning) and Tensorflow (deep learning) and witness its transformative power with real-world data sets by comparing these results. Let us begin!
Regularization is a critical concept in machine learning and deep learning that aims to prevent overfitting of models.
Overfitting occurs when a model learns the training data too well. The situation shows that their model is too good to be true.
Let's see what overfitting looks like.
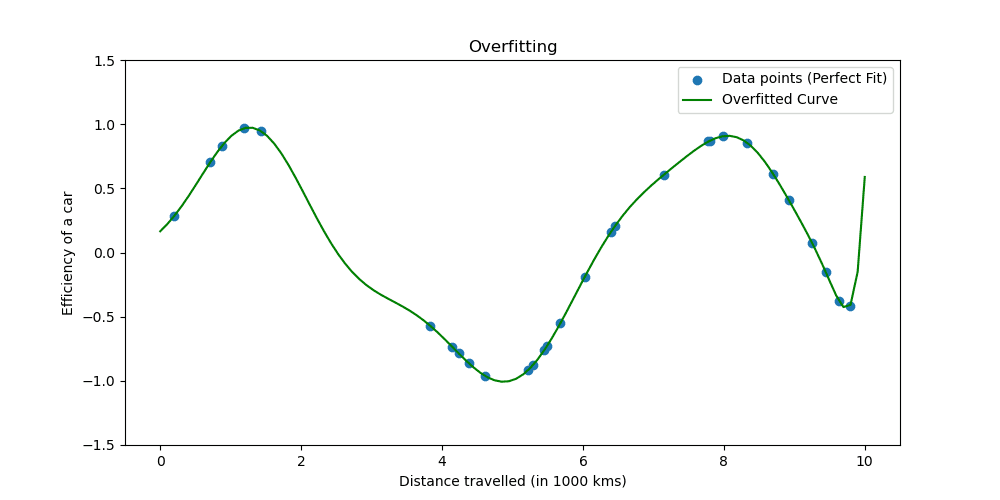

Regularization techniques adjust the learning process to simplify the model, ensuring that it performs well on the training data and generalizes well to new data. We will explore two well-known ways to do this.
In machine learning, regularization is often applied to linear models, such as linear and logistic regression. In this context, the most common forms of regularization are:
- L1 regularization (Lasso regression)
- L2 regularization (ridge regression)
Loop regularization It encourages the model to use only the most essential features by allowing some coefficient values to be exactly zero, which can be particularly useful for feature selection.
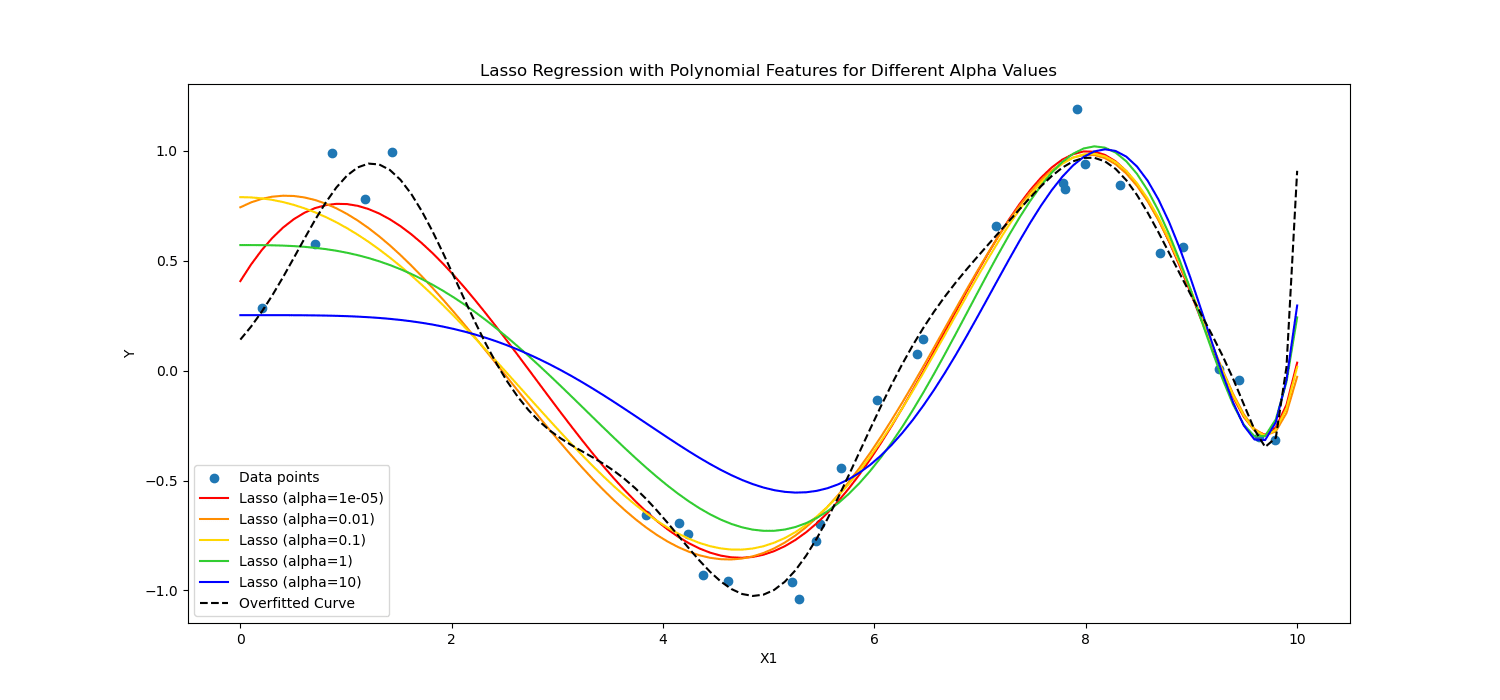

On the other hand, Ridge regularization discourages significant coefficients by penalizing the square of their values.
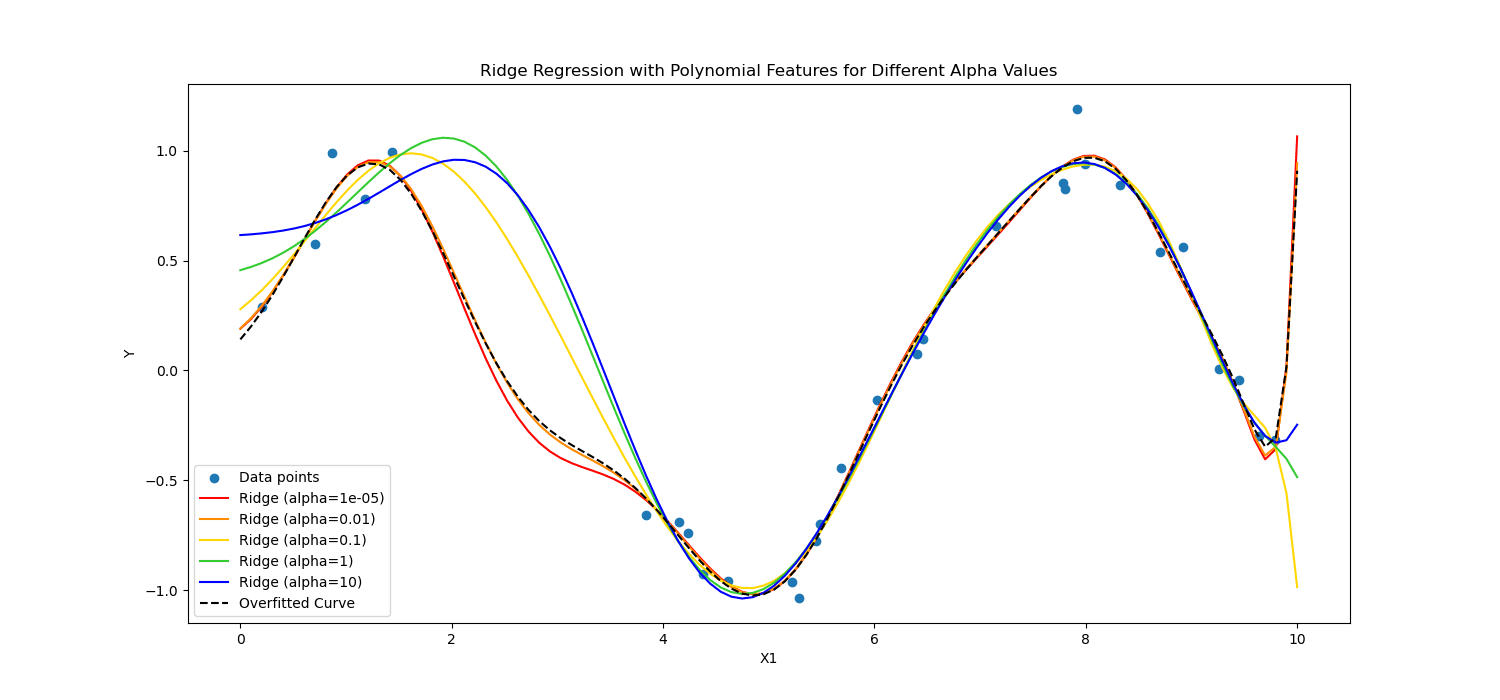

In short, they calculated differently.
Let's apply this to cardiac patient data to see its power in deep learning and machine learning.
Now, we will apply regularization to analyze the data of cardiac patients and see the power of regularization. You can access the data set from here.
To apply machine learning, we will use Scikit-learn; To apply deep learning, we will use TensorFlow. Let us begin!
Regularization in Machine Learning
Scikit-learn is one of the most popular Python Libraries for machine learning that provides simple and efficient data analysis and modeling tools.
It includes implementations of several regularization techniques, particularly for linear models.
Here, we will explore how to apply L1 (Lasso) and L2 (Ridge) regularization.
In the following code, we will train logistic regression using Ridge (L2) and Lasso (L1) regularization techniques. At the end we will see the detailed report. Let's look at the code.
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
# Assuming heart_data is already loaded
X = heart_data.drop('target', axis=1)
y = heart_data('target')
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# Define regularization values to explore
regularization_values = (0.001, 0.01, 0.1)
# Placeholder for storing performance metrics
performance_metrics = ()
# Iterate over regularization values for L1 and L2
for C_value in regularization_values:
# Train and evaluate L1 model
log_reg_l1 = LogisticRegression(penalty='l1', C=C_value, solver="liblinear")
log_reg_l1.fit(X_train_scaled, y_train)
y_pred_l1 = log_reg_l1.predict(X_test_scaled)
accuracy_l1 = accuracy_score(y_test, y_pred_l1)
report_l1 = classification_report(y_test, y_pred_l1)
performance_metrics.append(('L1', C_value, accuracy_l1))
# Train and evaluate L2 model
log_reg_l2 = LogisticRegression(penalty='l2', C=C_value, solver="liblinear")
log_reg_l2.fit(X_train_scaled, y_train)
y_pred_l2 = log_reg_l2.predict(X_test_scaled)
accuracy_l2 = accuracy_score(y_test, y_pred_l2)
report_l2 = classification_report(y_test, y_pred_l2)
performance_metrics.append(('L2', C_value, accuracy_l2))
# Print the performance metrics for all models
print("Model Performance Evaluation:")
print("--------------------------------")
for metric in performance_metrics:
reg_type, C_value, accuracy = metric
print(f"Regularization: {reg_type}, C: {C_value}, Accuracy: {accuracy:.2f}")
Here is the result.
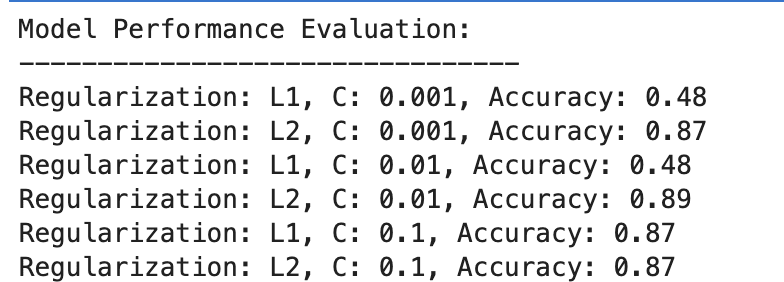

Let's evaluate the result.
L1 Regularization
- With C=0.001, the precision is notably low (48%). This shows that the model does not fit sufficiently. Shows too much regularization.
- As C increases to 0.01, the accuracy remains unchanged for L1, suggesting that the model still suffers from underfitting or that the regularization is too strong.
- With C = 0.1, the accuracy improves significantly to 87%, showing that reducing the strength of regularization allows the model to learn better from the data.
L2 Regularization
Overall, L2 regularization performs consistently well, with an accuracy of 87% for C=0.001 and slightly above 89% for C=0.01, and then plateaus at 87% for C=0.1.
This suggests that L2 regularization is generally more forgiving and effective for this data set in logistic regression models, potentially due to its nature.
Regularization in deep learning
Various regularization techniques are used in deep learning, including L1 (Lasso) and L2 (Ridge) regularization, dropout, and early stopping.
In this one, to repeat what we did before in the machine learning example, we will apply L1 and L2 regularization. This time let's define a list of L1 and L2 regularization values.
Then for all these values we will train and evaluate our deep learning model and at the end we will evaluate the results.
Let's look at the code.
from tensorflow.keras.regularizers import l1_l2
import numpy as np
# Define a list/grid of L1 and L2 regularization values
l1_values = (0.001, 0.01, 0.1)
l2_values = (0.001, 0.01, 0.1)
# Placeholder for storing performance metrics
performance_metrics = ()
# Iterate over all combinations of L1 and L2 values
for l1_val in l1_values:
for l2_val in l2_values:
# Define model with the current combination of L1 and L2
model = Sequential((
Dense(128, activation='relu', input_shape=(X_train_scaled.shape(1),), kernel_regularizer=l1_l2(l1=l1_val, l2=l2_val)),
Dropout(0.5),
Dense(64, activation='relu', kernel_regularizer=l1_l2(l1=l1_val, l2=l2_val)),
Dropout(0.5),
Dense(1, activation='sigmoid')
))
model.compile(optimizer="adam", loss="binary_crossentropy", metrics=('accuracy'))
# Train the model
history = model.fit(X_train_scaled, y_train, validation_split=0.2, epochs=100, batch_size=10, verbose=0)
# Evaluate the model
loss, accuracy = model.evaluate(X_test_scaled, y_test, verbose=0)
# Store the performance along with the regularization values
performance_metrics.append((l1_val, l2_val, accuracy))
# Find the best performing model
best_performance = max(performance_metrics, key=lambda x: x(2))
best_l1, best_l2, best_accuracy = best_performance
# After the loop, to print all performance metrics
print("All Model Performances:")
print("L1 Value | L2 Value | Accuracy")
for metrics in performance_metrics:
print(f"{metrics(0):<8} | {metrics(1):<8} | {metrics(2):.3f}")
# After finding the best performance, to print the best model details
print("\nBest Model Performance:")
print("----------------------------")
print(f"Best L1 value: {best_l1}")
print(f"Best L2 value: {best_l2}")
print(f"Best accuracy: {best_accuracy:.3f}")
Here is the result.
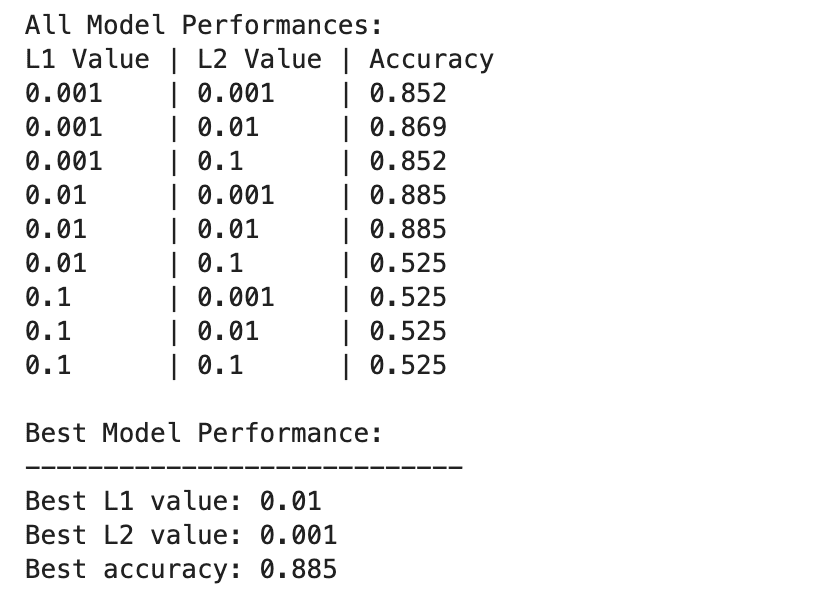

Deep learning model performance varies more widely between different combinations of L1 and L2 regularization values.
The best performance is observed at L1=0.01 and L2=0.001, with an accuracy of 88.5%, indicating a balanced regularization that prevents overfitting while allowing the model to capture underlying patterns in the data. .
Higher regularization values, especially at L1=0.1 or L2=0.1, dramatically reduce the model's accuracy to 52.5%, suggesting that too much regularization severely limits the model's learning ability.
Machine learning and deep learning in regularization
Let's compare the results between Machine Learning and Deep Learning.
Regularization Effectiveness: In both machine learning and deep learning contexts, proper regularization helps mitigate overfitting, but overregularization leads to underfitting. The optimal regularization strength varies, and deep learning models potentially require a more nuanced trade-off due to their greater complexity.
Performance: The best performing machine learning model (L2 with C=0.01, 89% accuracy) and the best performing deep learning model (L1=0.01, L2=0.001, 88.5% accuracy) achieve comparable accuracies, demonstrating that both approaches can be effective. regularized to achieve high performance on this data set.
Regularization Strategy: L2 regularization appears to be more effective and less sensitive to the choice of C in logistic regression models, while a combination of L1 and L2 regularization provides the best result in deep learning, offering a balance between feature selection and weight penalty.
The choice and strength of regularization must be carefully adjusted to balance the complexity of learning with the risk of overfitting or underfitting.
Throughout this exploration, we have demystified regularization, showing its role in preventing overfitting and ensuring that our models generalize well to unseen data.
Applying regularization techniques will bring you closer to proficiency in machine learning and deep learning, solidifying your data scientist toolset.
Go to data projects and try to regularize your data in different scenarios such as Delivery duration prediction. We use machine learning and deep learning models in this data project. However, at the end we also mentioned that there could be room for improvement. So why don't you try regularization there and see if it helps you?
Nate Rosidi He is a data scientist and in product strategy. He is also an adjunct professor of analysis and is the founder of StrataScratch, a platform that helps data scientists prepare for their interviews with real questions from top companies. Connect with him on Twitter: StrataScratch either LinkedIn.






