Introduction
Imagine that you are conducting a study to determine whether a new drug effectively lowers blood pressure. You give the drug to a group of patients and compare their results to those of a control group given a placebo. You analyze the data and conclude that the new drug significantly lowers blood pressure when, in fact, it does not. This incorrect rejection of the null hypothesis (that the drug has no effect) is a type I error. On the other hand, suppose that the drug actually lowers blood pressure, but your study fails to detect this effect because of insufficient sample size or variability in the data. As a result, you conclude that the drug is ineffective, which is a type II error.
These scenarios highlight the importance of understanding Type I and Type II errors in statistical testing. Type I errors, also known as false positives, occur when we mistakenly reject a true null hypothesis. Type II errors, or false negatives, occur when we fail to reject a false null hypothesis. Much of statistical theory revolves around minimizing these errors, even though eliminating them completely is statistically impossible. By understanding these concepts, we can make more informed decisions in a variety of fields, from medical testing to quality control in manufacturing.
General description
- Type I and Type II errors represent false positives and false negatives in hypothesis testing.
- Hypothesis testing involves formulating null and alternative hypotheses, choosing a significance level, calculating test statistics, and making decisions based on critical values.
- Type I errors occur when a true null hypothesis is mistakenly rejected, leading to unnecessary interventions.
- Type II errors occur when a false null hypothesis is not rejected, leading to misdiagnoses or overlooked effects.
- Balancing type I and type II errors requires trade-offs in significance levels, sample sizes, and test power to effectively minimize both errors.
The Basics of Hypothesis Testing
Hypothesis testing is a method used to decide whether there is sufficient evidence to reject a null hypothesis (H₀) in favor of an alternative hypothesis (H₁). The process involves:
- Hypothesis formulation
- No effect or no difference: No effect or no difference.
- Alternative hypothesis (H₁): There is an effect or a difference.
- Choosing a significance level (α): The probability threshold for rejecting H₀ is typically set to 0.05, 0.01, or 0.10.
- Calculation of the test statistic: A value derived from sample data that is used to compare with a critical value.
- Making a decision: If the test statistic exceeds the crucial value, reject H₀; otherwise, do not reject H₀.
Read also: End-to-end statistics for data science
Type 1 error (false positive)
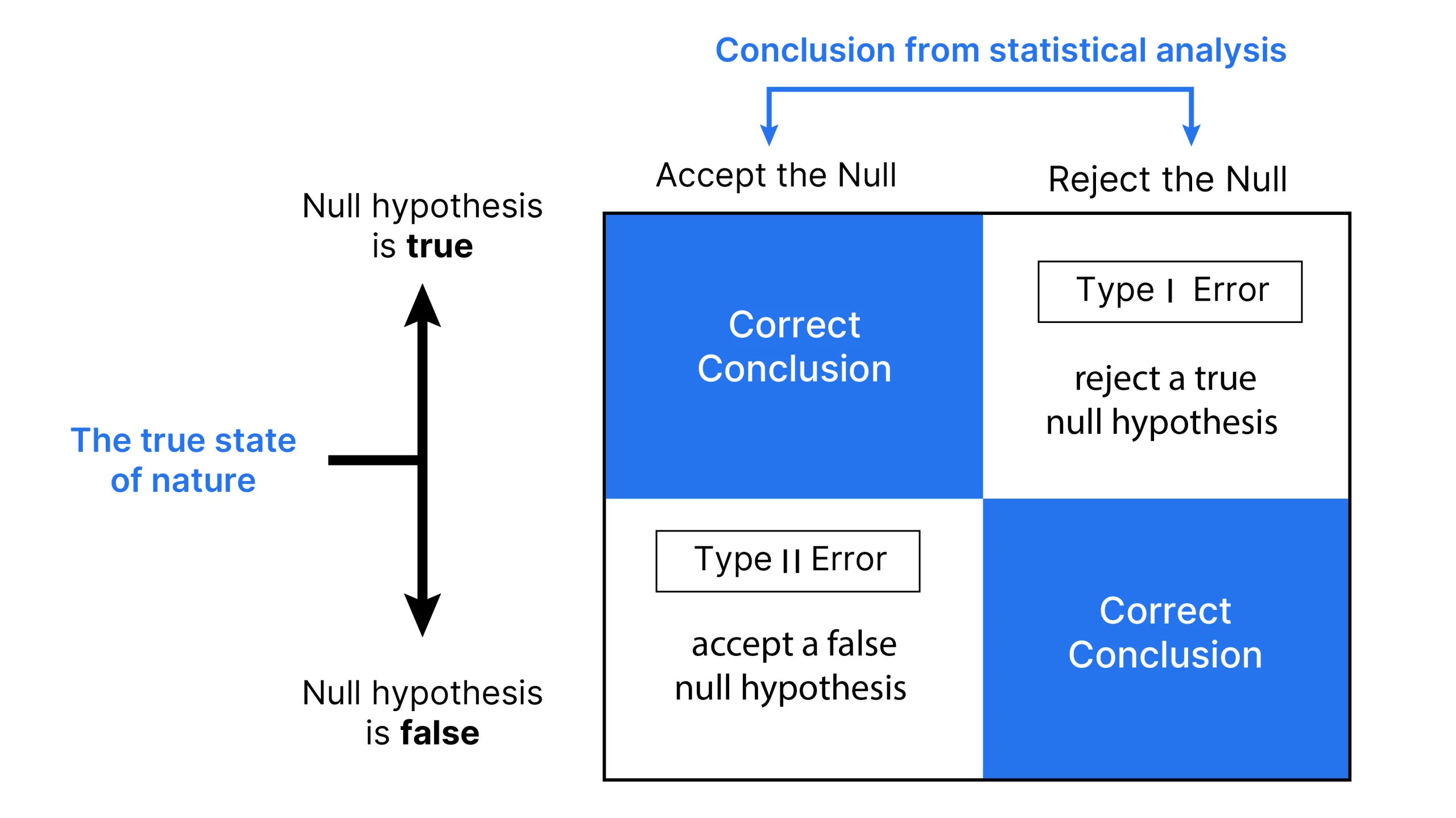
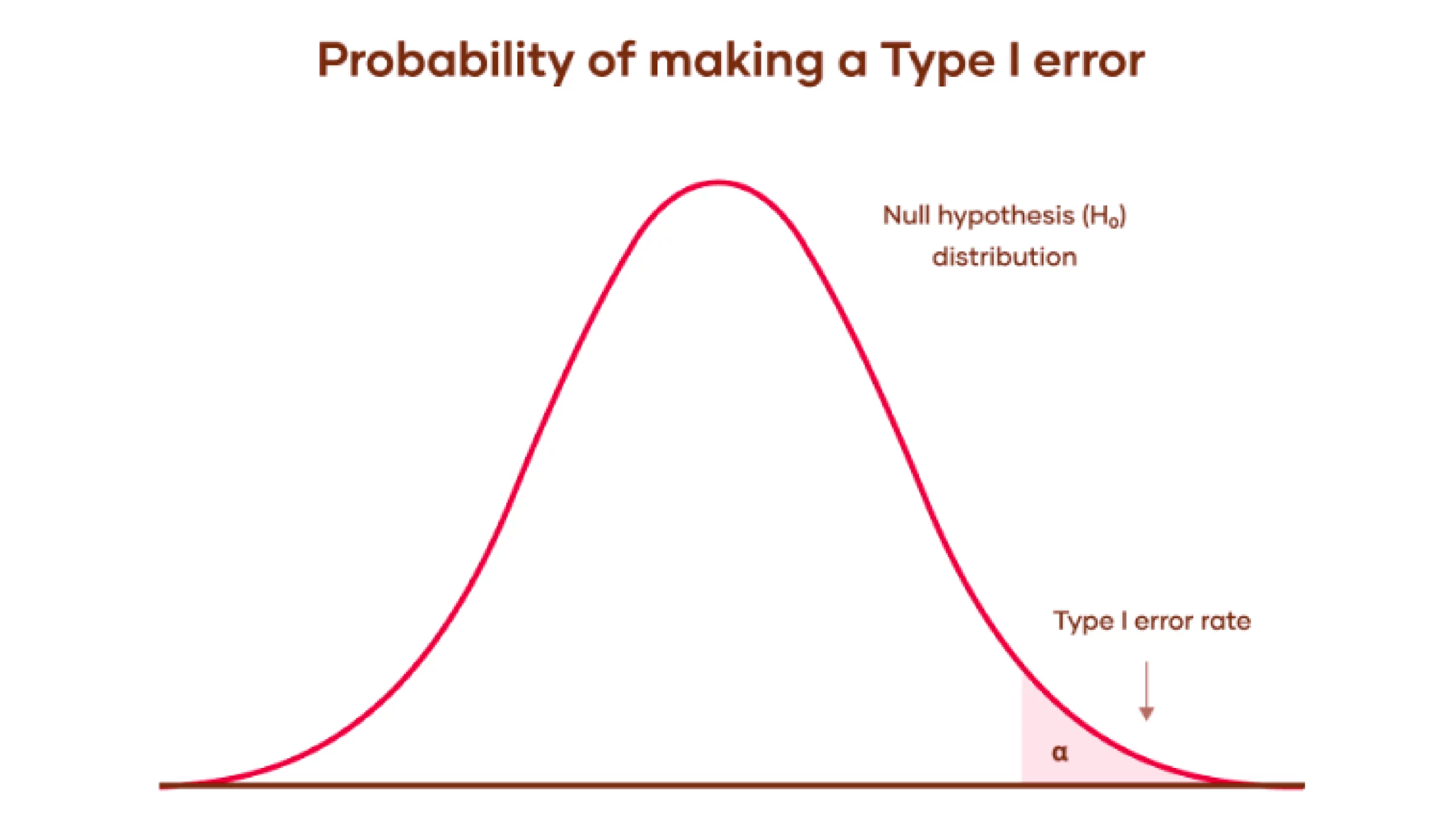
A type I error occurs when the null hypothesis (H0) of an experiment is true but is mistakenly rejected (graph mentioned below).
This error represents the identification of something that is not actually present, similar to a false positive. This can be explained in simple terms with an example: in a medical test to detect a disease, a type I error would mean that the test indicates that a patient has the disease when they do not, essentially generating a false alarm. In this case, the null hypothesis (H0) would state: the patient does not have the disease.
The probability of making a type I error is called the significance level or rate level. It is denoted by the Greek letter α (alpha) and is known as the alpha level. Typically, this chance or probability is set at 0.05 or 5%. Thus, researchers are often inclined to accept a 5% chance of incorrectly rejecting the null hypothesis when it is honestly true.
Type I errors can lead to unnecessary treatments or interventions, causing stress and possible harm to people.
Let's understand this with Graph:
- Null hypothesis distribution: The bell curve shows the range of possible outcomes if the null hypothesis is true. This means that the results are due to chance without any real effect or difference.
- Type I error rate: The shaded area under the tail of the curve. represents the level of significance, α. It is the probability of rejecting the null hypothesis when it is actually true. Which results in a type I error (false positive).
Type 2 error (false negative)
A type II error occurs when a valid alternative is used hypothesis In simpler terms, it is like not detecting a bear that is there and therefore not raising the alarm when necessary. In this scenario, the null hypothesis (H0) still says, “There is no bear.” The researcher commits a type II error if a bear is present but not detected.
The fundamental difficulty is not always whether the disease exists, but whether it is diagnosed correctly. Error can arise in two ways: either by not detecting the disease when it is present or by trying to detect it when it is not present.
The probability of type II error is denoted by the Greek letter β (beta). This value is related to the statistical power of a test, which is calculated as 1 minus β (1−β).
Type II errors can lead to misdiagnoses or missed effects, leading to inappropriate treatments or interventions.
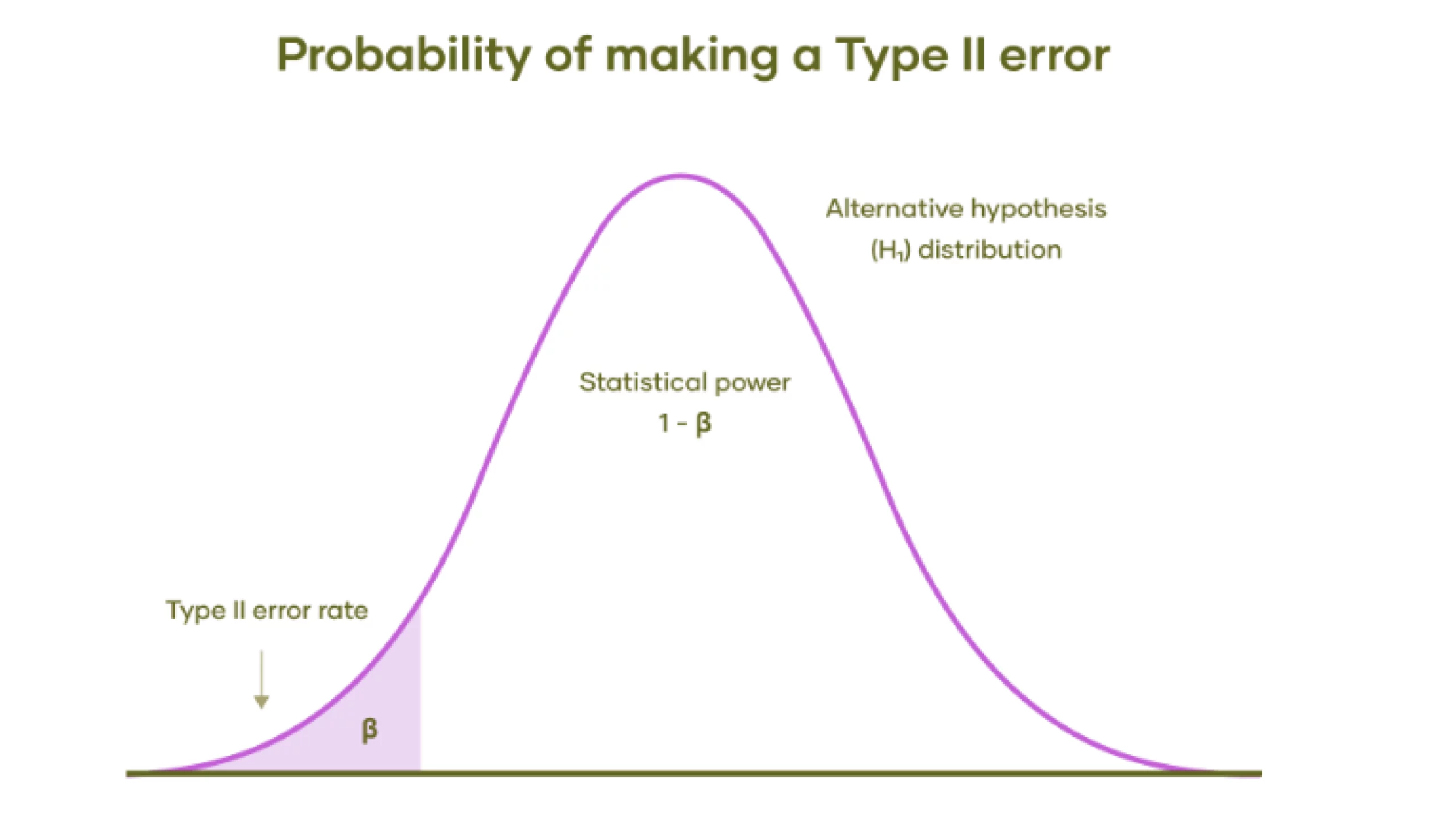
Let's understand this with Graph:
- Distribution of alternative hypothesis: The bell curve represents the range of possible outcomes if the alternative hypothesis is true. This means that there is a real effect or difference, contrary to the null hypothesis.
- Type II error rate (β): The shaded area under the left tail of the distribution represents the probability of a type II error.
- Statistical power (1 – β): The unshaded area under the curve to the right of the shaded area represents the statistical power of the test. Statistical power is the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true. Greater power means a lower probability of making a type II error.
Read also: Learn all about hypothesis testing!
Comparison of type I and type II errors
Here is the detailed comparison:
| Aspect | Type I error | Type II error |
|---|---|---|
| Definition and terminology | Reject a true null hypothesis (false positive) | Accepting a false null hypothesis (false negative) |
| Symbolic representation | α (alpha) | β (beta) |
| Probability and significance | Equal to the significance level established for the test | Calculated as 1 minus the power of the test (1 – power) |
| Error reduction strategies | Decreases the level of significance (increases type II errors) | Increase the level of significance (increases type I errors) |
| Casual factors | Chance or luck | Smaller sample sizes or less powerful statistical tests |
| Analogies | “False hit” in a detection system | “Miss” in a detection system |
| Association of hypotheses | Incorrectly rejecting the null hypothesis | Do not reject a false null hypothesis |
| Conditions of occurrence | It occurs when acceptance levels are too lenient. | It occurs when the acceptance criteria are too strict. |
| Transcendence | Prioritised in fields where avoiding false positives is crucial (e.g. clinical trials) | Prioritised in fields where avoiding false negatives is crucial (e.g. detection of serious diseases) |
Read also: Simplified hypothesis testing for data science beginners
Trade-off between type I and type II errors
In general, there is a trade-off between Type I and Type II errors: reducing the probability of one type of error generally increases the likelihood of the opposite type occurring.
- Significance level (α): Decreasing α reduces the probability of a type I error, but increases the risk of a type II error. Increasing α has the opposite effect.
- Sample size: Increasing the sample size can reduce type I and type II errors, as larger samples provide more precise estimates.
- Test power: Improving the power of the test by increasing the sample size or using more sensitive tests can reduce the likelihood of type II errors.
Conclusion
Type I and Type II errors are fundamental concepts in statistics and research techniques. By knowing the difference between these errors and their implications, we can better interpret research results, conduct more robust research, and make more informed decisions in a variety of fields. Remember that the goal is not to eliminate errors (which is impossible), but to successfully manage them based on the particular context and potential outcomes.
Frequent questions
Answer: It is difficult to eliminate both types of errors because reducing one often increases the other. However, by increasing the sample size and carefully designing the study, researchers can reduce both errors to applicable levels.
Answer: The following are the most common misconceptions about Type I and Type II errors:
Wrong idea: A lower α always means a better test.
Reality: While a lower α reduces type I errors, it may increase type II errors, leading to true effects not being detected.
Wrong idea: Large sample sizes eliminate the need to worry about these errors.
Fact: Large sample sizes reduce errors, but do not eliminate them. Good study design remains essential.
Wrong idea: A significant result (p-value < α) means that the null hypothesis is false.
Reality: A significant result suggests evidence against H₀, but does not prove that H₀ is false. Other factors such as the study design and context must be considered.
Answer: Increasing the power of the test increases the probability of detecting a true effect. You can do this by:
A. Increase the sample size.
B. Using more precise measurements.
C. Reduce the variability of your data.
D. Increase the effect size, if possible.
Answer: Pilot studies help you estimate the parameters needed to design a larger, definitive study. They provide initial data on effect sizes and variability, which inform your sample size calculations and help balance type I and type II errors in the main study.





