What is KL divergence that revolutionized machine learning?

Introduction

Few concepts from mathematics and information theory have had such a profound impact on modern machine learning and artificial intelligence as Kullback–Leibler (KL) divergence. This powerful metric, called relative entropy or information gain, has become indispensable in a number of fields, from statistical inference to deep learning. In this article, we’ll delve into the world of KL divergence, exploring its origins, applications, and why it has become such a crucial concept in the era of big data and ai.

General description

• KL divergence quantifies the difference between two probability distributions.
• It requires two probability distributions and has revolutionized fields such as machine learning and information theory.
• Measures the additional information needed to encode data from one distribution using another.
• KL divergence is crucial for training diffusion models, optimizing noise distribution, and improving text-to-image generation.
• It is valued for its solid theoretical basis, flexibility, scalability and interpretability in complex models.

Introduction to KL divergence

KL Divergence measures the difference between two probability distributions. Imagine you have two ways of describing the same event, perhaps two different models that predict the weather. KL divergence gives you a way to quantify how much these two descriptions differ.

Mathematically, for discrete probability distributions P and Q, the KL divergence from Q to P is defined as:

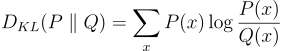
Where the sum is taken over all possible values ​​of x.

This formula may seem intimidating at first, but its interpretation is quite intuitive. It measures the average amount of additional information needed to encode data coming from P when using a code optimized for Q.

Kuala Lumpur Divergence: Requirements and Revolutionary Impact

To calculate KL divergence, you need:

• Two probability distributions over the same set of events
• A way of calculating logarithms (usually base 2 or natural logarithm)

With just these ingredients, KL divergence has revolutionized several fields:

• Machine Learning: In areas such as variational inference and generative models (e.g., variational autoencoders), it measures how well a model approximates the actual distribution of data.
• Information theory: Provides a fundamental measure of information content and compression efficiency.
• Statistical inference: It is crucial in hypothesis testing and model selection.
• Natural language processing: It is used in topic modeling and evaluation of language models.
• Reinforcement learning: Assists in optimizing exploration policies and strategies.

How does KL divergence work?

To truly understand KL divergence, let's break it down step by step:

• Comparing probabilities: We observe the probability of each possible event under the P and Q distributions.
• Taking the proportion: We divide P(x) by Q(x) to see how much more (or less) likely each event is under P compared to Q.
• Logarithmic scale: We calculate the logarithm of this ratio. This step is crucial because it ensures that the divergence is always non-negative and zero only when P and Q are identical.
• Weighing: We multiply this logarithm by P(x), giving more weight to events that are more likely at P.
• Summarizing: Finally, we sum these weighted logarithms for all possible events.

The result is a single number that tells us how different P and Q are. Importantly, KL divergence is not symmetric: DKL(P || Q) is generally not equal to DKL(Q || P). This asymmetry is actually a feature, not a bug, because it allows KL divergence to capture the direction of the difference between distributions.

The role of KL divergence in diffusion models

One of the most interesting recent applications of KL divergence is diffusion models, a class of generative models that have taken the ai ​​world by storm. Diffusion models, such as DALL-E 2, Stable Diffusion, and Halfwayhave revolutionized image generation, producing incredibly realistic and creative images from text descriptions.

This is how KL divergence plays a crucial role in diffusion models:

• Training process: Diffusion model training measures the difference between the actual noise distribution and the estimated noise distribution at each step of the diffusion process. This helps the model learn to reverse the diffusion process effectively.
• Variational lower bound: The training objective of diffusion models typically involves minimizing a variational lower bound, which includes its terms. This ensures that the model learns to generate samples that closely match the data distribution.
• Regularization of latent space: It helps to regularize the latent space of diffusion models, ensuring that the learned representations are well behaved and can be easily sampled.
• Model comparison: Researchers use it to compare different diffusion and variant models, helping to identify which approaches are most effective at capturing the true distribution of data.
• Conditional generation: In text-to-image models, KL divergence measures how well the generated images match the text descriptions, guiding the model to produce more accurate and relevant results.

The success of diffusion models in generating diverse, high-quality images is a testament to the power of KL divergence in capturing complex probability distributions. As these models evolve, they remain a critical tool for pushing the boundaries of what is possible in ai-generated content.

This addition updates the article with one of the most interesting recent applications of KL divergence, making it even more relevant and engaging for readers interested in cutting-edge ai technologies. The section fits well with the overall structure of the article and provides a concrete example of how it is used in an innovative application that many readers may have heard of or even interacted with.

Read also: Stable diffusion artificial intelligence has conquered the world

Why is KL divergence better?

KL divergence has several advantages that make it superior to other metrics in many scenarios:

• Theoretical basis of information: It has a solid foundation in information theory, which makes it interpretable in terms of bits of information.
• Flexibility: It can be applied to both discrete and continuous distributions.
• Scalability: It works well in high-dimensional spaces, making it suitable for complex machine learning models.
• Theoretical properties: It satisfies important mathematical properties such as nonnegativity and convexity, which makes it useful in optimization problems.
• Interpretability: The asymmetry of KL divergence can be intuitively understood in terms of compression and encoding.

Interacting with the divergence of Kuala Lumpur

To truly appreciate the power of KL divergence, consider its applications in everyday scenarios:

• Recommendation systems: When Netflix suggests movies you might like, it often uses this technique to measure how well its model predicts your preferences.
• Image generation: What impressive ai-generated images do you see on the Internet? Many come from models trained with this theory to measure how close the generated images are to real ones.
• Language models: The next time you're impressed by a chatbot's human-like responses, remember that KL divergence likely played a role in training its underlying language model.
• Climate modeling: Scientists use it to compare different climate models and assess their reliability in predicting future weather patterns.
• Financial risk assessment: Banks and insurance companies use this theory in their risk models to make more accurate predictions about market behavior.

Conclusion

KL divergence transcends mathematics and aids machine understanding and market predictions, making it essential in our data-driven world.

As we continue to push the boundaries of artificial intelligence and data analytics, HeThis theory will undoubtedly play an even more crucial role. Whether you are a data scientist, a machine learning enthusiast, or just someone curious about the mathematical foundations of our digital age, understanding it opens a fascinating window into how we quantify, compare, and learn from information.

So the next time you marvel at an ai-generated piece of art or receive a surprisingly accurate product recommendation, take a moment to appreciate the elegant mathematics of KL divergence working behind the scenes, quietly revolutionizing the way we process and understand information in the 21st century.

Frequent questions