What is hinge loss in machine learning?

Hinge loss is critical in classification tasks and is widely used in support vector machines (SVMs), quantifying errors by penalizing predictions near or across decision boundaries. By promoting strong margins between classes, it improves the generalization of the model. This guide explores the fundamentals of hinge loss, its mathematical basis, and its applications, aimed at both beginners and advanced machine learning enthusiasts.

What is loss in machine learning?

In machine learning, loss describes how well a model's prediction matches actual target values. In fact, it quantifies the error between the predicted result and the ground truth and also feeds the model during training. Minimizing loss functions is essentially the main goal when training machine learning models.

Key points about loss

1. Purpose of loss:
   • Loss functions are used to guide the optimization process during training.
   • They help the model learn optimal weights by penalizing incorrect predictions.
2. Difference between loss and cost:
   • Loss: It refers to the error of a single training example.
   • Cost: It refers to the average loss over the entire data set (sometimes used interchangeably with the term “objective function”).
3. Types of loss functions: Loss functions vary depending on the type of task:
   • Regression problems: mean square error (MSE), mean absolute error (MAE).
   • Classification problems: cross entropy loss, hinge loss, Kullback–Leibler divergence.

What is hinge loss?

Hinge Loss is a specific type of loss function that is mainly used for classification tasks, especially in support vector machines (SVM). It measures how well a model's predictions align with actual labels and encourages predictions that are not only correct but confidently separated by a margin.

Hinge loss penalizes predictions that are:

1. Incorrectly classified.
2. Correctly classified but too close to the decision boundary (within a “margin”).

It is designed to create a “margin” around the decision boundary to improve the robustness of the classifier.

Formula

The hinge loss for a single data point is given by:

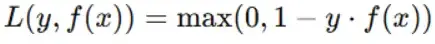
Where:

• y: actual label of the data point, either +1 or −1 (SVMs require binary labels in this format).
• f(x): predicted score (for example, the raw output of the model before applying a decision threshold).
• max⁡(0,…): guarantees that the loss is not negative.

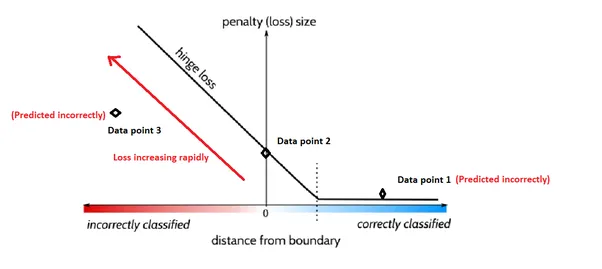
How does it work?

1. Correct and safe prediction (yf(x)>=1):
   • No loss is incurred because the prediction is correct and beyond the margin.
   • L(y,f(x))=0.
2. Correct but not secure (0
   • The prediction is penalized for being within the range but on the correct side of the decision boundary.
   • The loss is proportional to how far off the margin the prediction is.

3. Incorrect prediction (y⋅f(x)≤0):
   • The prediction is on the wrong side of the decision boundary.
   • The loss grows linearly with the magnitude of the error.

Advantages of hinge loss

These are the advantages of Hindge Loss:

• Margin maximization: Hinge loss helps maximize the decision boundary margin, which is crucial for support vector machines (SVMs). This leads to better generalization performance and robustness against overfitting.
• Binary classification: Hinge loss is very effective for binary classification tasks and works well with linear classifiers.
• Scattered Gradients: When the prediction is correct within a margin (i.e., y⋅f(x)>1), the hinge loss gradient is zero. This sparsity can improve computational efficiency during training.
• Theoretical Guarantees: Hinge loss is based on strong theoretical foundations in margin-based classification, making it widely accepted in machine learning research and practice.
• Robustness to outliers: Outliers that are correctly classified by a large margin do not contribute additional losses, reducing their impact on the model.
• Support for linear and non-linear models: While it is a key component of linear SVMs, hinge loss can also be extended to nonlinear SVMs with kernel tricks.

Disadvantages of hinge loss

These are the disadvantages of hinge loss:

• For binary classification only: Hinge loss is mainly designed for binary classification tasks and cannot directly handle multi-class classification without modifications, such as using the multi-class SVM variant.
• Non-differentiability: The hinge loss is not differentiable at the point y⋅f(x)=1, which can complicate optimization and require the use of subgradient methods instead of standard gradient-based optimization.
• Sensitive to imbalanced data: Hinge loss inherently does not account for class imbalance, potentially leading to biased decision boundaries in data sets with unequal class distributions.
• Does not provide probabilistic results: Unlike loss functions such as cross entropy, hinge loss does not produce probabilistic results, which limits its use in applications that require calibrated probabilities.
• Less robust for noisy data: Hinge loss is more sensitive to misclassified data points near the decision boundary, which can degrade performance in the presence of noisy labels.
• No direct support for neural networks: While hinge loss can be used in neural networks, it is less common because other loss functions (e.g., cross entropy) are typically preferred for their compatibility with probabilistic results and ease of optimization.
• Limited scalability: Computing hinge loss for large-scale data sets, particularly for kernel-based SVMs, can be computationally expensive compared to simpler loss functions.

Python implementation

from sklearn.svm import LinearSVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import numpy as np


# Step 1: Generate synthetic data
# Creating a dataset with 1,000 samples and 10 features for binary classification
x, y = make_classification(n_samples=1000, n_features=10, n_informative=8, n_redundant=2, random_state=42)
y = (y * 2) - 1  # Convert labels from {0, 1} to {-1, +1} as required by hinge loss


# Step 2: Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)


# Step 3: Initialize the LinearSVC model
# Using hinge loss, which is the foundation of SVM classifiers
model = LinearSVC(loss="hinge", max_iter=1000, random_state=42)


# Step 4: Train the model
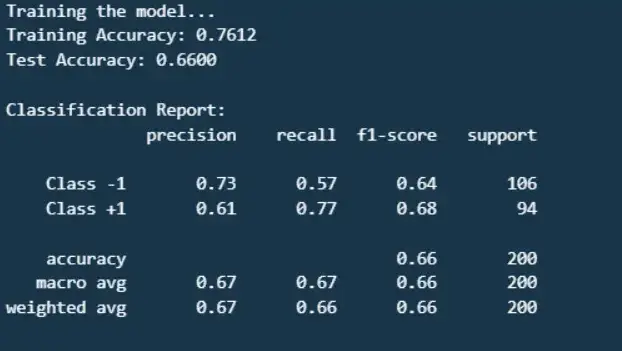
print("Training the model...")
model.fit(X_train, y_train)


# Step 5: Evaluate the model
# Calculate accuracy on training and testing data
train_accuracy = model.score(X_train, y_train)
test_accuracy = model.score(X_test, y_test)


print(f"Training Accuracy: {train_accuracy:.4f}")
print(f"Test Accuracy: {test_accuracy:.4f}")


# Step 6: Detailed evaluation
# Predict labels for the test set
y_pred = model.predict(X_test)


# Generate a classification report
print("\nClassification Report:")
print(classification_report(y_test, y_pred, target_names=("Class -1", "Class +1")))

Conclusion

Hinge loss plays an important role in machine learning, especially when considering classification problems with SVM. Hinge loss functions impose penalties on those classifications that are incorrect or as close as possible to a decision boundary. The models make better generalizations and become stronger due to hinge loss, whose unique properties are, for example, the ability to maximize margin and produce sparse gradients.

However, like any loss function, hinge loss has its limitations, such as nondifferentiability and sensitivity to imbalanced data. Understanding these trade-offs is important for choosing the appropriate loss function for a specific application. Although hinge loss is fundamental to SVMs, its principles and applications reach elsewhere, making it a versatile and comprehensive machine learning algorithm.

Hinge loss forms a solid foundation for developing robust classifiers using both theoretical understanding and practical implementation. Whether you're a beginner or a seasoned professional, mastering hinge loss will help you develop a better ability to design effective machine learning models with the right amount of precision you need.

If you are looking for an online ai/ML course, explore: The Certified ai & ML BlackBelt Plus Program

Frequently asked questions