What are joint, marginal and conditional probability?

Probability is a cornerstone of statistics and data science, providing a framework for quantifying uncertainty and making predictions. Understanding joint, marginal, and conditional probability is essential for analyzing events in both independent and dependent scenarios. This article discusses these concepts with clear explanations and examples.

What is probability?

Probability measures the probability of an event occurring, expressed as a value between 0 and 1:

• 0: The event is impossible.
• 1: The event is safe.

For example, tossing a fair coin has a 0.5 probability of getting heads.

Joint probability

Joint probability refers to the probability of two (or more) events occurring simultaneously. For events A and B, it is denoted as:

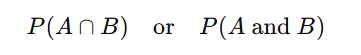
Formula:

P(A∩B)=P(A∣B)⋅P(B)=P(B∣A)⋅P(A)

Example

Consider rolling a die and flipping a coin:

• Event A: Rolling a 4 (probability = 1\6​)
• Event B: Throwing a head (probability = 1\2​)

If the events are independent:

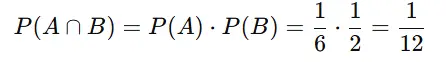
Marginal probability

Marginal probability is the probability that a single event will occur, regardless of other events. It is obtained by adding the joint probabilities involving that event.

For event A:

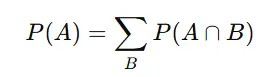
Example

Consider a data set of students:

• 60% are men (P(Male)=0.6).
• 30% play basketball (P(Basketball)=0.3).
• 20% are males who play basketball (P(Male∩Basketball)=0.2).

The marginal probability of being a man:

P(Male)=0.6

Conditional probability

Conditional probability measures the probability that an event will occur given that another event has already occurred. For events A and B, it is denoted as:

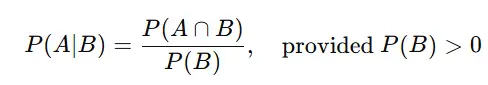
Example

From the student data set:

• P(Men∩Basketball)=0.2P
• P(basketball)=0.3

The probability that a student is male given that he plays basketball:

P(Male∣Basketball)=P(Male∩Basketball)/P(Basketball)=0.2/0.3=0.67

This means that 67% of basketball players are men.

Relationships between joint, marginal and conditional probabilities

1. Joint probability and marginal probability
   • Joint probability considers multiple events together.
   • Marginal probability considers a single event, which often adds up to joint probabilities.
2. Joint probability and conditional probability
   • The joint probability can be expressed by conditional probability:
     P(A∩B)=P(A∣B)⋅P(B)
3. Marginal and conditional probability
   • Marginal probability can help calculate conditional probabilities and vice versa.

Python implementation

Here is a Python implementation of joint, marginal and conditional probability using simple examples:

# Import necessary library
import numpy as np
import pandas as pd

# Example 1: Joint and Marginal Probabilities
# Simulating a dataset of students
data = {
    'Gender': ('Male', 'Male', 'Male', 'Female', 'Female', 'Female'),
    'Basketball': ('Yes', 'No', 'Yes', 'Yes', 'No', 'No')
}

# Create a DataFrame
df = pd.DataFrame(data)

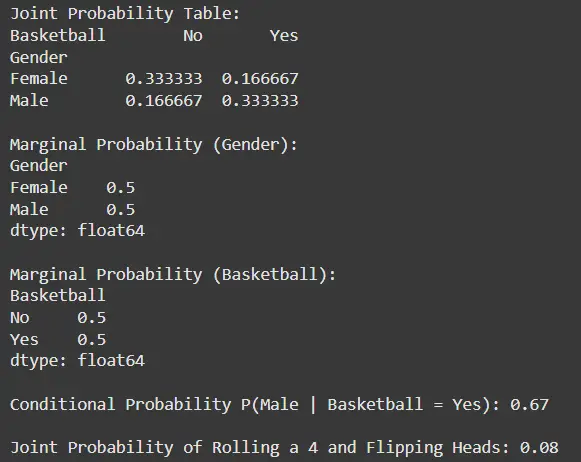
# Frequency table (Joint Probability Table)
joint_prob_table = pd.crosstab(df('Gender'), df('Basketball'), normalize="all")
print("Joint Probability Table:")
print(joint_prob_table)

# Marginal probabilities
marginal_gender = joint_prob_table.sum(axis=1)
marginal_basketball = joint_prob_table.sum(axis=0)

print("\nMarginal Probability (Gender):")
print(marginal_gender)

print("\nMarginal Probability (Basketball):")
print(marginal_basketball)

# Example 2: Conditional Probability
# P(Male | Basketball = Yes)
joint_male_yes = joint_prob_table.loc('Male', 'Yes')  # P(Male and Basketball = Yes)
prob_yes = marginal_basketball('Yes')  # P(Basketball = Yes)

conditional_prob_male_given_yes = joint_male_yes / prob_yes
print(f"\nConditional Probability P(Male | Basketball = Yes): {conditional_prob_male_given_yes:.2f}")

# Example 3: Joint Probability for Independent Events
# Rolling a die and flipping a coin
P_roll_4 = 1/6  # Probability of rolling a 4
P_flip_heads = 1/2  # Probability of flipping heads

joint_prob_roll_and_heads = P_roll_4 * P_flip_heads
print(f"\nJoint Probability of Rolling a 4 and Flipping Heads: {joint_prob_roll_and_heads:.2f}")

Applications in real life

1. medical diagnosis
   • Joint probability: He probability of having a disease and showing specific symptoms.
   • Marginal probability: The overall probability of having the disease.
   • Conditional probability: The probability of having the disease given the symptoms.
2. Machine learning
   • It is used in Naive Bayes classifiers, where conditional probabilities are calculated for classification tasks.
3. Risk analysis
   • Understand dependencies between events, such as in financial markets or insurance.

Conclusion

Understanding joint, marginal, and conditional probabilities is crucial for solving real-world problems involving uncertainty and dependencies. These concepts form the basis of advanced topics in statistics, machine learning, and decision making under uncertainty. Mastery of these principles allows for effective analysis and informed conclusions.

Frequently asked questions

Hi, I'm Janvi, a data science enthusiast currently working at Analytics Vidhya. My journey into the world of data began with a deep curiosity about how we can extract meaningful insights from complex data sets.