Introduction
Imagine watching a drop of ink slowly spread across a blank page, its color slowly diffusing through the paper until it becomes a beautiful, intricate pattern. This natural process of diffusion, where particles move from areas of high concentration to low concentration, is the inspiration behind diffusion models in machine learning. Just as the ink spreads and blends, diffusion models work by gradually adding and then removing noise from data to generate high-quality results.
In this article, we will explore the fascinating world of diffusion models, unraveling how they transform noise into detailed outputs, their unique methodologies, and their growing applications in fields like image generation, data denoising, and more. By the end, you’ll have a clear understanding of how these models mimic natural processes to achieve remarkable results in various domains.
Overview
- Understand the core principles and mechanics behind diffusion models.
- Explore how diffusion models convert noise into high-quality data outputs.
- Learn about the applications of diffusion models in image generation and data denoising.
- Identify key differences between diffusion models and other generative models.
- Gain insights into the challenges and advancements in the field of diffusion modeling.
What are Diffusion Models?
Diffusion models are inspired by the natural process where particles spread from areas of high concentration to low concentration until they are evenly distributed. This principle is seen in everyday examples, like the gradual dispersal of perfume in a room.
In the context of machine learning, diffusion models use a similar idea by starting with data and progressively adding noise to it. They then learn to reverse this process, effectively removing the noise and reconstructing the data or creating new, realistic versions. This gradual transformation results in detailed and high-quality outputs, useful in fields such as medical imaging, autonomous driving, and generating realistic images or text.
The unique aspect of diffusion models is their step-by-step refinement approach, which allows them to achieve highly accurate and nuanced results by mimicking natural processes of diffusion.
How Do Diffusion Models Work?
Diffusion models operate through a two-phase process: first, a neural network is trained to add noise to data (known as the forward diffusion phase), and then it learns to systematically reverse this process to recover the original data or generate new samples. Here’s an overview of the stages involved in a diffusion model’s functioning.
Data Preparation
Before starting the diffusion process, the data must be prepared correctly for training. This preparation includes steps like cleaning the data to remove anomalies, normalizing features to maintain consistency, and augmenting the dataset to enhance variety—especially important for image data. Standardization is used to ensure a normal distribution, which helps manage noisy data effectively. Different types of data, such as text or images, may require specific adjustments, such as addressing imbalances in data classes. Proper data preparation is crucial for providing the model with high-quality input, allowing it to learn significant patterns and produce realistic outputs during use.
Forward Diffusion Process : Transforming Images to Noise
The forward diffusion process starts by drawing from a simple distribution, typically Gaussian. This initial sample is then progressively altered through a sequence of reversible steps, each adding a bit more complexity via a Markov chain. As these transformations are applied, structured noise is incrementally introduced, allowing the model to learn and replicate the intricate patterns present in the target data distribution. The purpose of this process is to evolve the basic sample into one that closely resembles the complexity of the desired data. This approach demonstrates how beginning with simple inputs can result in rich, detailed outputs.
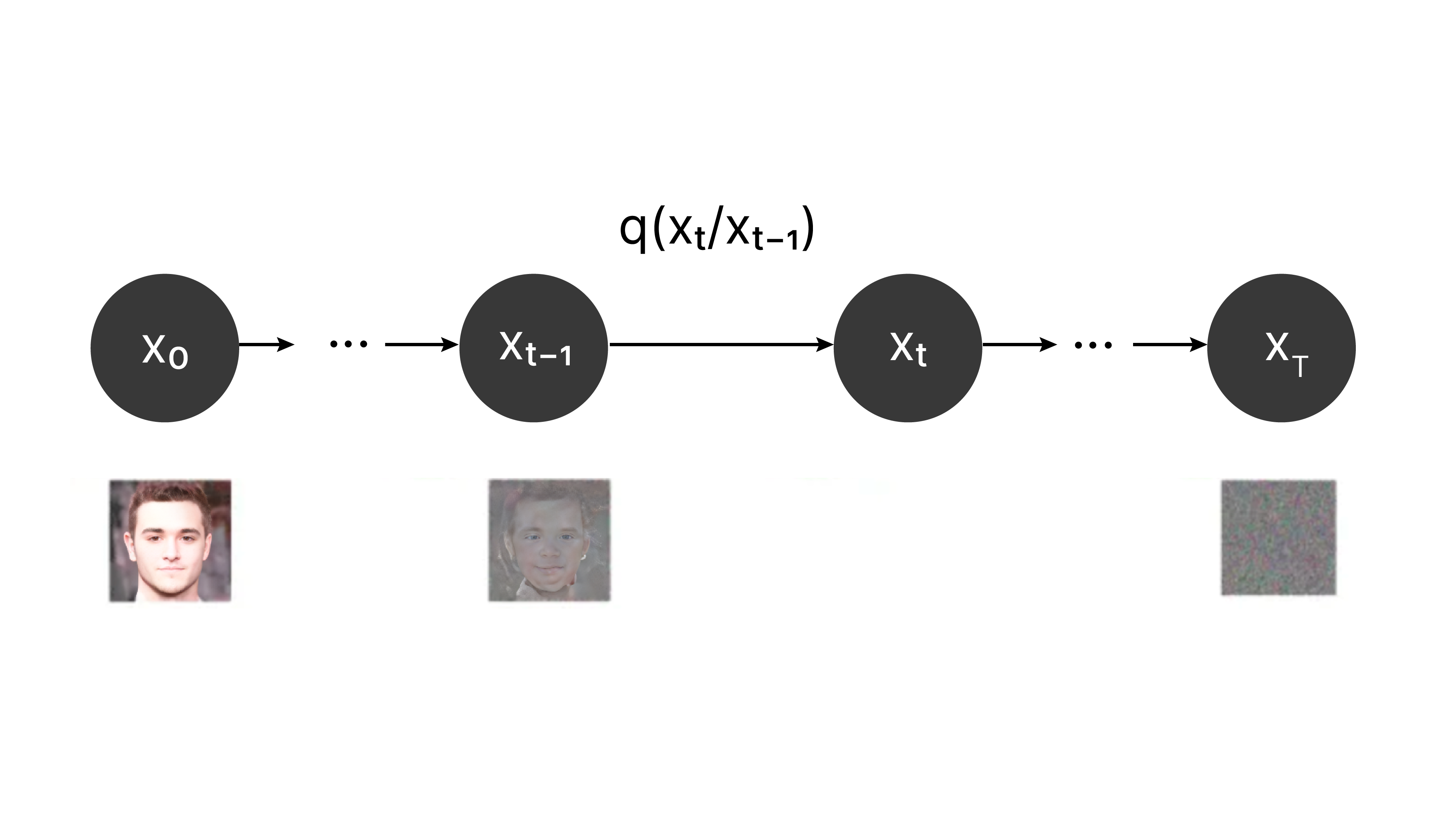
Mathematical Formulation
Let x0 represent the initial data (e.g., an image). The forward process generates a series of noisy versions of this data x1,x2,…,xT through the following iterative equation:
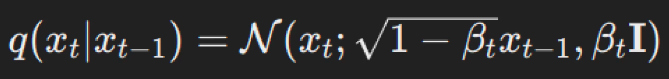
Here,q is our forward process, and xt is the output of the forward pass at step t. N is a normal distribution, 1-txt-1 is our mean, and tI defines variance.
Reverse Diffusion Process : Transforming Noise to Image
The reverse diffusion process aims to convert pure noise into a clean image by iteratively removing noise. Training a diffusion model is to learn the reverse diffusion process so that it can reconstruct an image from pure noise. If you guys are familiar with GANs, we’re trying to train our generator network, but the only difference is that the diffusion network does an easier job because it doesn’t have to do all the work in one step. Instead, it uses multiple steps to remove noise at a time, which is more efficient and easy to train, as figured out by the authors of this paper.
Mathematical Foundation of Reverse Diffusion
- Markov Chain: The diffusion process is modeled as a Markov chain, where each step only depends on the previous state.
- Gaussian Noise: The noise removed (and added) is typically Gaussian, characterized by its mean and variance.
The reverse diffusion process aims to reconstruct x0 from xT, the noisy data at the final step. This process is modeled by the conditional distribution:
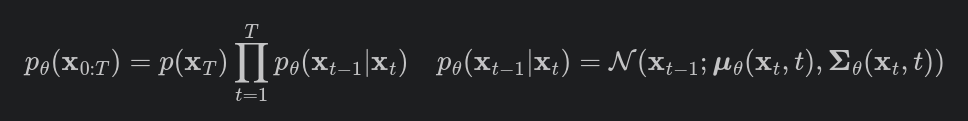
where:
- μθ(xt,t)is the mean predicted by the model,
- σθ2
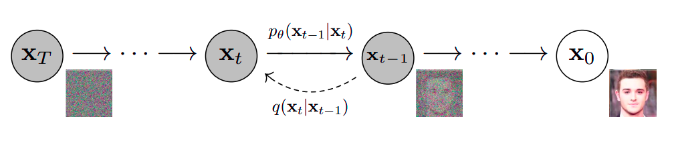
The above image depicts the reverse diffusion process often used in generative models.
Starting from noise xT, the process iteratively denoises the image through time steps T to 0. At each step t, a slightly less noisy version xt−1 is predicted from the noisy input xt using a learned model pθ(xt−1∣xt).
The dashed arrow labeled ( q(x_t \mid x_{t-1}) ) shows the forward diffusion process, while the solid arrow ( p_\theta(x_{t-1} \mid x_t) ) shows the reverse process that the model learns and estimates.
Implementation of How diffusion Model Works
We will now look into the steps of how diffusion model works.
Step1: Import Libraries
import torch
import torch.nn as nn
import torch.optim as optimStep2: Define the Diffusion Model
class DiffusionModel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(DiffusionModel, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_dim, hidden_dim)
self.fc3 = nn.Linear(hidden_dim, output_dim)
def forward(self, noise_signal):
x = self.fc1(noise_signal)
x = self.relu(x)
x = self.fc2(x)
x = self.relu(x)
x = self.fc3(x)
return xDefines a neural network model for the diffusion process with:
- Three Linear Layers
- ReLU Activations
Step3: Initialize the Model and Optimizer
input_dim = 100
hidden_dim = 128
output_dim = 100
batch_size = 64
num_epochs = 5
model = DiffusionModel(input_dim, hidden_dim, output_dim)
optimizer = optim.Adam(model.parameters(), lr=0.001)
criterion = nn.MSELoss()
data_loader = ((torch.randn(batch_size, input_dim), torch.randn(batch_size, output_dim))) * 10
target_data = torch.randn(batch_size, output_dim)
- Sets dimensions for input, hidden, and output layers.
- Creates an instance of the DiffusionModel.
- Initializes the Adam optimizer with a learning rate of 0.001.
Training Loop:
for epoch in range(num_epochs):
epoch_loss = 0
for batch_data, target_data in data_loader:
# Generate a random noise signal
noise_signal = torch.randn(batch_size, input_dim)
# Forward pass through the model
generated_data = model(noise_signal)
# Compute loss and backpropagate
loss = criterion(generated_data, target_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_loss += loss.item()
# Print the average loss for this epoch
print(f'Epoch ({epoch + 1}/{num_epochs}), Loss: {epoch_loss / len(data_loader):.4f}')
Epoch Loop: Runs through the specified number of epochs.
Batch Loop: Processes each batch of data.
- Noise Signal
- Forward Pass
- Compute Loss
- Backpropagation
- Accumulate Loss
Diffusion Model Techniques
Let us now discuss diffusion model techniques.
Denoising Diffusion Probabilistic Models (DDPMs)
DDPMs are one of the most widely recognized types of diffusion models. The core idea is to train a model to reverse a diffusion process, which gradually adds noise to data until all structure is destroyed, converting it to pure noise. The reverse process then learns to denoise step-by-step, reconstructing the original data.
Forward Process
This is a Markov chain where Gaussian noise is sequentially added to a data sample over a series of time steps. This process continues until the data becomes indistinguishable from random noise.
Reverse Process
The reverse process, which is also a Markov chain, learns to undo the noise added in the forward process. It starts from pure noise and progressively denoises to generate a sample that resembles the original data.
Training
The model is trained using a variant of a variational lower bound on the negative log-likelihood of the data. This involves learning the parameters of a neural network that predicts the noise added at each step.

Score-Based Generative Models (SBGMs)
Score-based generative models use the concept of a “score function,” which is the gradient of the log probability density of data. The score function provides a way to understand how the data is distributed.
Score Matching
The model is trained to estimate the score function at different noise levels. This involves learning a neural network that can predict the gradient of the log probability at various scales of noise.
Langevin Dynamics
Once the score function learns, the process generates samples by starting with random noise and gradually denoising it using Langevin dynamics. This Markov Chain Monte Carlo (MCMC) method uses the score function to move towards higher-density regions.

Stochastic Differential Equations (SDEs)
In this approach, diffusion models are treated as continuous-time stochastic processes, described by SDEs.
Forward SDE
The forward process is described by an SDE that continuously adds noise to data over time. The drift and diffusion coefficients of the SDE dictate how the data evolves into noise.
Reverse-Time SDE
The reverse process is another SDE that goes in the opposite direction, transforming noise back into data by “reversing” the forward SDE. This requires knowing the score (the gradient of the log density of data).
Numerical Solvers
Numerical solvers like Euler-Maruyama or stochastic Runge-Kutta methods are used to solve these SDEs for generating samples.

Noise Conditional Score Networks (NCSN)
NCSN implements score-based models where the score network conditions on the noise level.
Noise Conditioning
The model predicts the score (i.e., the gradient of the log-density of data) for different levels of noise. This is done using a noise-conditioned neural network.
Sampling with Langevin Dynamics
Similar to other score-based models, NCSNs generate samples using Langevin dynamics, which iteratively denoises samples by following the learned score.
Variational Diffusion Models (VDMs)
VDMs combine the diffusion process with variational inference, a technique from Bayesian statistics, to create a more flexible generative model.
Variational Inference
The model uses a variational approximation to the posterior distribution of latent variables. This approximation allows for efficient computation of likelihoods and posterior samples.
Diffusion Process
The diffusion process adds noise to the latent variables in a way that facilitates easy sampling and inference.
Optimization
The training process optimizes a variational lower bound to efficiently learn the diffusion process parameters.
Implicit Diffusion Models
Unlike explicit diffusion models like DDPMs, implicit diffusion models do not explicitly define a forward or reverse diffusion process.
Implicit Modeling
These models might leverage adversarial training techniques (like GANs) or other implicit methods to learn the data distribution. They do not require the explicit definition of a forward process that adds noise and a reverse process that removes it.
Applications
They are useful when the explicit formulation of a diffusion process is difficult or when combining the strengths of diffusion models with other generative modeling techniques, such as adversarial methods.
Augmented Diffusion Models
Researchers enhance standard diffusion models by introducing modifications to improve performance.
Modifications
Changes could involve altering the noise schedule (how noise levels distribute across time steps), using different neural network architectures, or incorporating additional conditioning information (e.g., class labels, text, etc.).
Goals
The modifications aim to achieve higher fidelity, better diversity, faster sampling, or more control over the generated samples.
GAN vs. Diffusion Model


| Aspect | GANs (Generative Adversarial Networks) | Diffusion Models |
| Architecture | Consists of a generator and a discriminator | Models the process of adding and removing noise |
| Training Process | Generator creates fake data to fool the discriminator; discriminator tries to distinguish real from fake data | Trains by learning to denoise data, gradually refining noisy inputs to recover original data |
| Strengths | Produces high-quality, realistic images; effective in various applications | Can generate high-quality images; more stable training; handles complex data distributions well |
| Challenges | Training can be unstable; prone to mode collapse | Computationally intensive; longer generation time due to multiple denoising steps |
| Typical Use Cases | Image generation, style transfer, data augmentation | High-quality image generation, image inpainting, text-to-image synthesis |
| Generation Time | Generally faster compared to diffusion models | Slower due to multiple steps in the denoising process |
Applications of Diffusion Models
We will now explore applications of diffusion model in detail.
Image Generation
Diffusion models excel in generating high-quality images. Artists have used them to create stunning, realistic artworks and generate images from textual descriptions.
Import Libraries
import torch
from diffusers import StableDiffusionPipelineSet Up Model and Device
model_id = "CompVis/stable-diffusion-v1-4"
device = "cuda"Load and Configure the Model
pipe = StableDiffusionPipeline.from_pretrained(model_id, torch_dtype=torch.float16)
pipe = pipe.to(device)Generate an Image
prompt = "a landscape with rivers and mountains"
image = pipe(prompt).images(0)Save the Image
image.save("Image.png")
Image-to-Image Translation
From changing day scenes to night to turning sketches into realistic images, diffusion models have proven their worth in image-to-image translation tasks.
Install Necessary Libraries
!pip install --quiet --upgrade diffusers transformers scipy ftfy
!pip install --quiet --upgrade accelerateImport Required Libraries
import torch
import requests
import urllib.parse as parse
import os
import requests
from PIL import Image
from diffusers import StableDiffusionDepth2ImgPipelineCreate and Initialize the Pipeline
pipe = StableDiffusionDepth2ImgPipeline.from_pretrained(
"stabilityai/stable-diffusion-2-depth",
torch_dtype=torch.float16,
)
# Assigning to GPU
pipe.to("cuda")Utility Functions for Handling Image URLs
def check_url(string):
try:
result = parse.urlparse(string)
return all((result.scheme, result.netloc, result.path))
except:
return False
# Load an image
def load_image(image_path):
if check_url(image_path):
return Image.open(requests.get(image_path, stream=True).raw)
elif os.path.exists(image_path):
return Image.open(image_path)
Load an Image from the Web
img = load_image("https://5.imimg.com/data5/AK/RA/MY-68428614/apple-500x500.jpg")
img
Set a Prompt
prompt = "Sketch them"Generate the Modified Image
pipe(prompt=prompt, image=img, negative_prompt=None, strength=0.7).images(0)
Image-to-image translation with diffusion models is a complex task that generally involves training the model on a specific dataset for a particular translation task. Diffusion models work by iteratively denoising a random noise signal to generate a desired output, such as a transformed image. However, training such models from scratch requires significant computational resources, so practitioners often use pre-trained models for practical applications.
In the provided code, the process is simplified and involves using a pre-trained diffusion model to modify an existing image based on a textual prompt.
- Library and Model Setup
- Image Loading and Preparation
- Text Prompt
Generating the Modified Image:The model takes the text prompt and the original image and performs iterative denoising, guided by the text, to generate a new image. This new image reflects the contents of the original image altered by the description in the text prompt.
Understanding Data Denoising
Diffusion models find applications in denoising noisy images and data. They can effectively remove noise while preserving essential information.
import numpy as np
import cv2
def denoise_diffusion(image):
grey_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
denoised_image = cv2.denoise_TVL1(grey_image, None, 30)
# Convert the denoised image back to color
denoised_image_color = cv2.cvtColor(denoised_image, cv2.COLOR_GRAY2BGR)
return denoised_image_color
# Load a noisy image
noisy_image = cv2.imread('noisy_image.jpg')
# Apply diffusion-based denoising
denoised_image = denoise_diffusion(noisy_image)
# Save the denoised image
cv2.imwrite('denoised_image.jpg', denoised_image)This code cleans up a noisy image, like a photo with a lot of tiny dots or graininess. It converts the noisy image to black and white, and then uses a special technique to remove the noise. Finally, it turns the cleaned-up image back to color and saves it. It’s like using a magic filter to make your photos look better.
Anomaly Detection and Data Synthesis
Detecting anomalies using diffusion models typically involves comparing how well the model reconstructs the input data. Anomalies are often data points that the model struggles to reconstruct accurately.
Here’s a simplified Python code example using a diffusion model to identify anomalies in a dataset
import numpy as np
import tensorflow as tf
from tensorflow import keras
from sklearn.model_selection import train_test_split
# Simulated dataset (replace this with your dataset)
data = np.random.normal(0, 1, (1000, 10)) # 1000 samples, 10 features
train_data, test_data = train_test_split(data, test_size=0.2, random_state=42)
# Build a diffusion model (replace with your specific model architecture)
input_shape = (10,) # Adjust this to match your data dimensionality
model = keras.Sequential((
keras.layers.Input(shape=input_shape),
# Add diffusion layers here
# Example: keras.layers.Dense(64, activation='relu'),
# keras.layers.Dense(10)
))
# Compile the model (customize the loss and optimizer as needed)
model.compile(optimizer="adam", loss="mean_squared_error")
# Train the diffusion model on the training data
model.fit(train_data, train_data, epochs=10, batch_size=32, validation_split=0.2)
reconstructed_data = model.predict(test_data)
# Calculate the reconstruction error for each data point
reconstruction_errors = np.mean(np.square(test_data - reconstructed_data), axis=1)
# Define a threshold for anomaly detection (you can adjust this)
threshold = 0.1
# Identify anomalies based on the reconstruction error
anomalies = np.where(reconstruction_errors > threshold)(0)
# Print the indices of anomalous data points
print("Anomalous data point indices:", anomalies)This Python code uses a diffusion model to find anomalies in data. It starts with a dataset and splits it into training and test sets. Then, it builds a model to understand the data and trains it. After training, the model tries to recreate the test data. Any data it struggles to recreate is marked as an anomaly based on a chosen threshold. This helps identify unusual or unexpected data points.
Benefits of Using Diffusion Models
Let us now look into the benefits of using diffusion models.
- High-Quality Image Generation: Diffusion models can produce highly detailed and realistic images.
- Fine-Grained Control: They allow for precise control over the image generation process, making them suitable for creating high-resolution images.
- No Mode Collapse: Diffusion models avoid issues like mode collapse, which is common in other models, leading to more diverse image outputs.
- Simpler Loss Functions: They use straightforward loss functions, making the training process more stable and less sensitive to tuning.
- Robustness to Data Variability: These models work well with different types of data, such as images, audio, and text.
- Better Handling of Noise: Their design makes them naturally good at tasks like denoising, which is useful for image restoration.
- Theoretical Foundations: Based on solid theoretical principles, diffusion models provide a clear understanding of their operations.
- Likelihood Maximization: They optimize data likelihood directly, ensuring quality in generated data.
- Capturing a Wide Range of Outputs: They capture a broad range of the data distribution, leading to diverse and varied results.
- Less Prone to Overfitting: The gradual transformation process helps prevent overfitting, maintaining coherence across different levels of detail.
- Flexibility and Scalability: Diffusion models can handle large datasets and complex models effectively, producing high-quality images.
- Modular and Extendable: Their architecture allows for easy modifications and scaling, making them adaptable to various research needs.
- Step-by-Step Generation: The process is interpretable, as it generates images gradually, which helps in understanding and improving the model’s performance.
Let us now look into popular diffusion tools below:
DALL-E 2
DALL-E 2, developed by OpenAI, is well known for producing incredibly imaginative and detailed graphics from written descriptions. It is a well-liked tool for creative and artistic reasons since it employs sophisticated diffusion techniques to create visuals that are both imaginative and realistic.
DALL-E 3
DALL-E 3, the most recent iteration of OpenAI’s image generating models, has notable improvements over DALL-E 2. Its inclusion into ChatGPT, which improves user accessibility, is a significant distinction. Additionally, DALL-E 3 has better image generating quality.
Sora
The newest model from OpenAI, Sora is the first to produce films from text descriptions. It is able to produce lifelike 1080p films up to one minute in length. To maintain ethical use and control over its distribution, Sora is now only available to a limited number of users.
Stable Diffusion
Stability ai created Stable Diffusion, which excels at translating text cues into lifelike pictures. It has gained recognition for producing images of excellent quality. Stable Diffusion 3, the most recent version, performs better at handling intricate suggestions and producing high-quality images. Outpainting is another aspect of Stable Diffusion that enables the expansion of an image beyond its initial bounds.
Midjourney
Another diffusion model that creates visuals in response to text instructions is called Midjourney. The most recent version, Midjourney v6, has drawn notice for its sophisticated image-creation capabilities. The only way to access Midjourney is via Discord, which makes it unique.
NovelAI Diffusion
With the help of NovelAI Diffusion, users can realize their imaginative ideas through a distinctive image creation experience. Important features are the ability to generate images from text and vice versa, as well as the ability to manipulate and renew images through inpainting.
Imagen
Google created Imagen, a text-to-image diffusion model renowned for its powerful language understanding and photorealism. It produces excellent visuals that closely match textual descriptions and uses huge transformer models for text encoding.
Challenges and Future Directions
While diffusion models hold great promise, they also present challenges:
- Complexity: Training and using diffusion models can be computationally intensive and complex.
- Large-Scale Deployment: Integrating diffusion models into practical applications at scale requires further development.
- Ethical Considerations: As with any ai technology, we must address ethical concerns regarding data usage and potential biases.
Conclusion
Diffusion models, inspired by the natural diffusion process where particles spread from high to low concentration areas, are a class of generative models. In machine learning, diffusion models gradually add noise to data and then learn to reverse this process to remove the noise, reconstructing or generating new data. They work by first training a model to add noise (forward diffusion) and then to systematically reverse this noise addition (reverse diffusion) to recover the original data or create new samples.
Key techniques include Denoising Diffusion Probabilistic Models (DDPMs), Score-Based Generative Models (SBGMs), and Stochastic Differential Equations (SDEs). These models are particularly useful in high-quality image generation, data denoising, anomaly detection, and image-to-image translation. Compared to GANs, diffusion models are more stable but slower due to their step-by-step denoising process.
To dive deeper into generative ai and diffusion models, check out the Pinnacle Program’s Generative ai Course for comprehensive learning.
Frequently Asked Questions
A. Diffusion models are generative models that simulate the natural diffusion process by gradually adding noise to data and then learning to reverse this process to generate new data or reconstruct original data.
A. Diffusion models add noise to data in a series of steps (forward process) and then train a model to remove the noise step by step (reverse process), effectively learning to generate or reconstruct data.
A. While diffusion models are popular in image generation, they can be applied to any data type where noise can be systematically added and removed, including text and audio.
A. SBGMs are diffusion models that learn to denoise data by estimating the gradient of the data distribution (score) and then generating samples by reversing the noise process.







