Generative diffusion models have revolutionized image and video generation, becoming the basis for next-generation generation software. While these models excel at handling complex, high-dimensional data distributions, they face a critical challenge: the risk of memorizing an entire training set in low-data scenarios. This memorization ability raises legal concerns, such as copyright laws, as these models could reproduce exact copies of training data instead of generating novel content. The challenge lies in understanding when these models truly generalize and when they simply memorize, especially considering that natural images generally have their variability confined to a small subspace of possible pixel values.
Recent research efforts have explored various aspects of the behavior and capabilities of diffusion models. Local intrinsic dimensionality (LID) estimation methods have been developed to understand how these models learn multiple data structures, focusing on analyzing the dimensional characteristics of individual data points. Some approaches examine how generalization emerges as a function of data set size and multiple variations of dimensions along diffusion trajectories. Additionally, statistical physics approaches are used to analyze the inverse process of diffusion models, as phase transitions and spectral gap analysis have been used to study generative processes. However, these methods either focus on exact scores or do not account for the interaction between memorization and generalization in diffusion models.
Researchers from Bocconi University, OnePlanet Research Center Donders Institute, RPI, JADS Tilburg University, IBM Research and the Donders Institute at Radboud University have extended the theory of memorization in generative diffusion to manifold-supported data using statistical physics. Their research reveals an unexpected phenomenon in which higher variance subspaces are more prone to memoization effects under certain conditions, leading to selective dimensionality reduction where key features of the data are retained without completely collapsing across points. individual training sessions. The theory presents a new understanding of how different tangent subspaces are affected by memorization at different critical times and data set sizes, and the effect depends on the variation of local data along specific directions.
The experimental validation of the proposed theory focuses on diffusion networks trained on multiple linear data structured with two different subspaces: one with high variance (1.0) and another with low variance (0.3). Spectral network analysis reveals behavioral patterns that align with theoretical predictions for different data set sizes and timing parameters. The network maintains a gap manifold that remains stable even at small time values for large data sets, suggesting a natural tendency toward generalization. The spectra show selective preservation of the low-variance gap while losing the high-variance subspace, matching theoretical predictions at intermediate data set sizes.
Experimental analysis of the MNIST, Cifar10, and Celeb10 data sets reveals distinct patterns in how latent dimensionality varies with data set size and diffusion time. The MNIST networks demonstrate clear spectral gaps, with dimensionality increasing from 400 data points to a high value of around 4000 points. While Cifar10 and Celeb10 show less clear spectral gaps, they show predictable changes in the spectral inflection points as the data set size varies. Furthermore, a notable finding is the growth of the unsaturated dimensionality of Cifar10, suggesting continued geometric memorization effects even with the full data set. These results validate theoretical predictions about the relationship between data set size and geometric memorization in different types of image data.
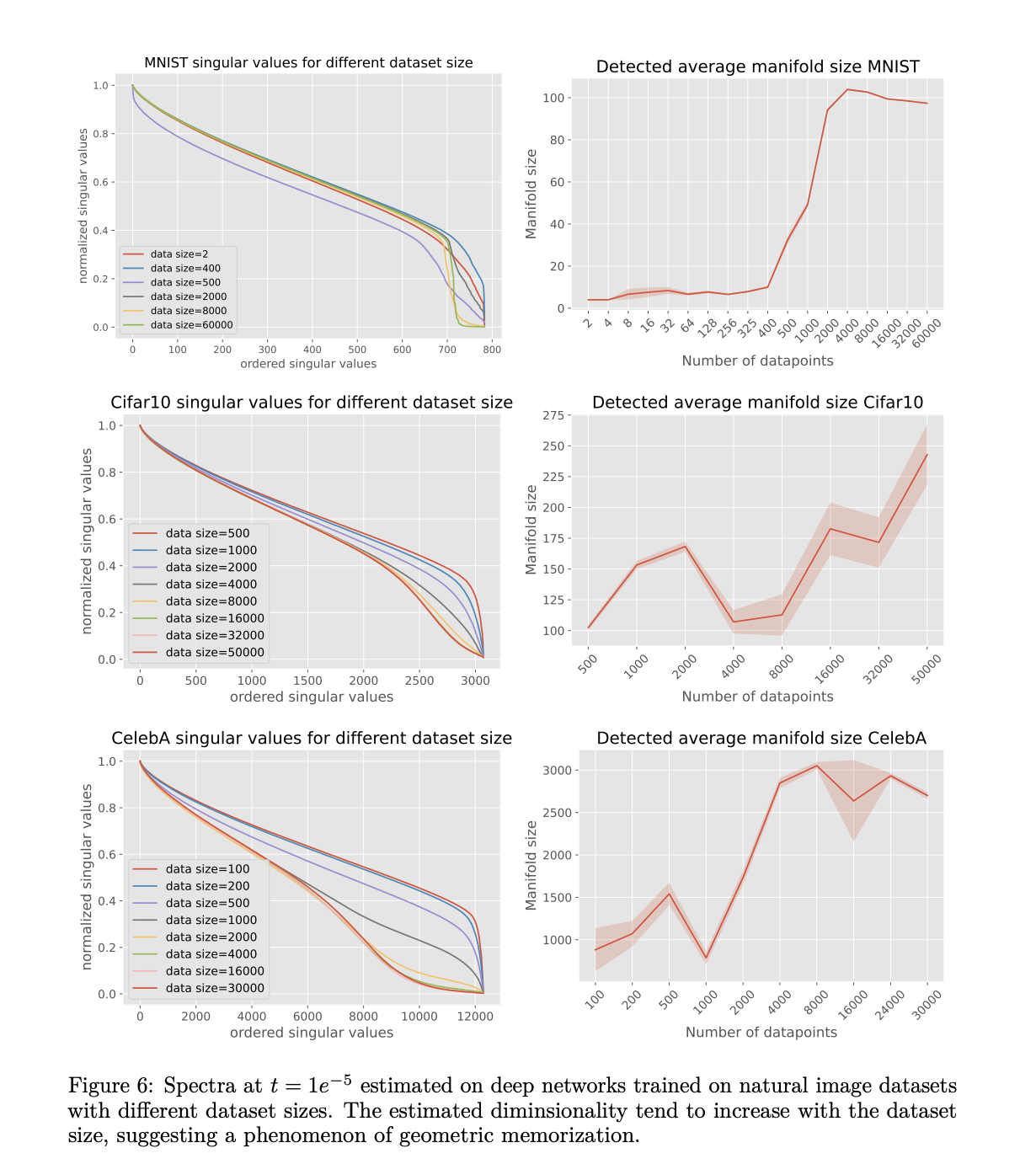
In conclusion, the researchers presented a theoretical framework for understanding generative diffusion models through the lens of statistical physics, differential geometry, and random matrix theory. The article contains crucial information on how these models balance memorization and generalization, especially in data set size and data variation patterns. While the current analysis focuses on empirical scoring functions, the theoretical framework lays the foundation for future research on the Jacobian spectra of trained models and their deviations from empirical predictions. These findings are valuable for advancing the understanding of the generalization capabilities of diffusion models, which is essential for their continued development.
look at the Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. If you like our work, you will love our information sheet.. Don't forget to join our SubReddit over 55,000ml.
(Sponsorship opportunity with us) Promote your research/product/webinar to over 1 million monthly readers and over 500,000 community members

Sajjad Ansari is a final year student of IIT Kharagpur. As a technology enthusiast, he delves into the practical applications of ai with a focus on understanding the impact of ai technologies and their real-world implications. Its goal is to articulate complex ai concepts in a clear and accessible way.
<script async src="//platform.twitter.com/widgets.js” charset=”utf-8″>






