Understanding and implementing genetic algorithms in Python

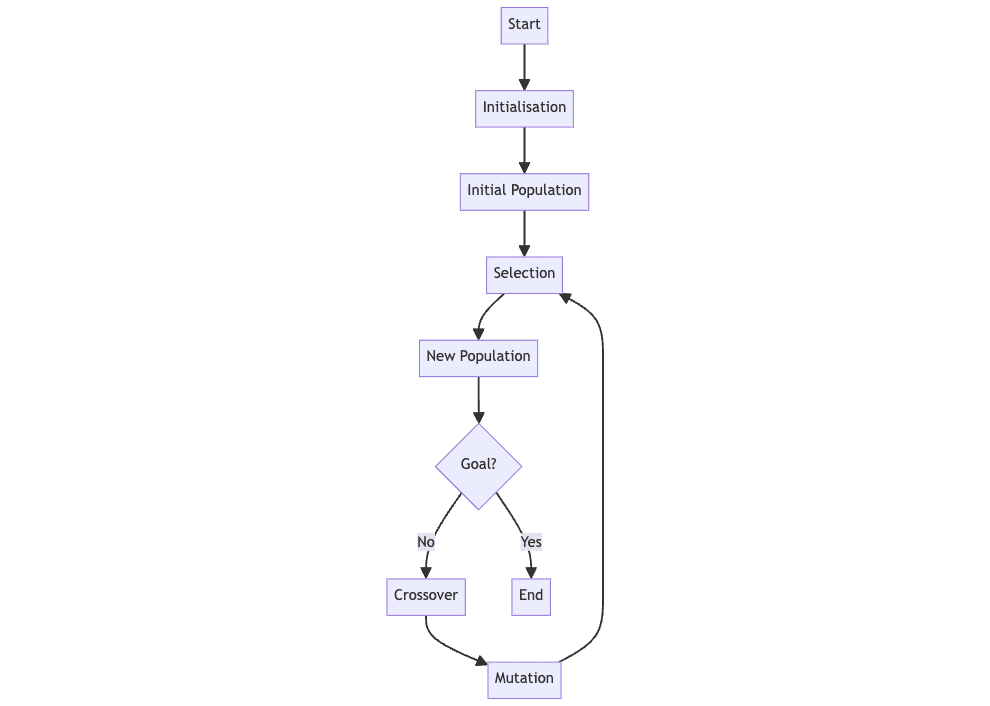
Genetic algorithms are techniques based on natural selection that are used to solve complex problems. They are used to arrive at reasonable solutions to the problem instead of other methods because the problems are complicated. In this article, we will cover the basics of genetic algorithms and how they can be implemented in Python.

Genetic components

Fitness function

The fitness function measures the proximity of a considered solution to the best possible solution to the problem. It provides a fitness level for each person in the population, which describes the quality or efficiency of the current generation. This score defines the choice, while the highest fitness value suggests an improved solution.
For example, suppose we are involved in the process of dealing with a real function, f(x) in which x is a set of parameters. The optimal value to find is x, so that f(x) assumes the largest value.

Selection

This is a process that defines which individuals within the current generation will be favored and thus reproduce and contribute to the next generation. It is possible to identify many selection methods and each of them has its own characteristics and appropriate contexts.

• Roulette wheel selection:
  Depending on the individual's fitness level, the probability of choosing the individual is also maximum.
• Tournament selection:
  A group is selected at random and the best of them is chosen.
• Rank-based selection:
  People are classified according to their physical fitness and selection chances are allocated proportionally based on their fitness scores.

Cross

Crossover is a basic concept of genetic algorithm that aims to exchange genetic information of two parental individuals to form one or more progeny. This process is very similar to the crossover and recombination of biology that occurs in nature. Applying the basic principles of inheritance, crossbreeding attempts to produce offspring that embody the desirable characteristics of the parents and therefore possess better adaptation in future generations. Crossover is a relatively broad concept that can be divided into several types, each of which has its peculiarities and the area in which it can be effectively applied.

• single point crossing: A crossover point is chosen on the parent chromosomes and only one crossover actually occurs. Before this position, all genes are taken from the first parent and all genes after this position are taken from the second parent.
• Two point crossing: Two breakpoints are selected and the part between them is exchanged between the two parent chromosomes. It also favors the exchange of genetic information rather than the crossing of a single point.

Mutation

In genetic algorithms, mutation is of utmost importance because it provides diversity, which is a crucial factor to avoid direct convergence towards the area of ​​optimal solutions. Therefore, obtaining random changes in the chain from an individual mutation allows the algorithm to go to other regions of the solution space that it cannot reach by crossover operations alone. This stochastic process ensures that no matter what happens, the population will evolve or change its position in the areas of the search space that have been identified as optimal by the genetic algorithm.

Steps to implement a genetic algorithm

Let's try to implement the genetic algorithm in Python.

Definition of the problem

Problem: Calculate on the specific function; f(x) = x^2f(x) = x^2; only integer values ​​of x.
Fitness function: for the case of a binary chromosome that is x, an example of the fitness function could be f(x)= x^2.

def fitness(chromosome):
    x = int(''.join(map(str, chromosome)), 2)
    return x ** 2

Population initialization

Generates a random chromosome of a given length.

def generate_chromosome(length):
    return (random.randint(0, 1) for _ in range(length))

def generate_population(size, chromosome_length):
    return (generate_chromosome(chromosome_length) for _ in range(size))

population_size = 10
chromosome_length = 5
population = generate_population(population_size, chromosome_length)

Physical Fitness Assessment

Evaluate the fitness of each chromosome in the population.

fitnesses = (fitness(chromosome) for chromosome in population)

Selection

Use selection roulette to select parental chromosomes based on their fitness.

def select_pair(population, fitnesses):
    total_fitness = sum(fitnesses)
    selection_probs = (f / total_fitness for f in fitnesses)
    parent1 = population(random.choices(range(len(population)), selection_probs)(0))
    parent2 = population(random.choices(range(len(population)), selection_probs)(0))
    return parent1, parent2

Cross

Use single-point crossover by choosing a random crossover position on the parent chain and swapping all genetic values ​​after this location between the two chains.

def crossover(parent1, parent2):
    point = random.randint(1, len(parent1) - 1)
    offspring1 = parent1(:point) + parent2(point:)
    offspring2 = parent2(:point) + parent1(point:)
    return offspring1, offspring2

Mutation

Implement the mutation by flipping bits with a certain probability.

def mutate(chromosome, mutation_rate):
    return (gene if random.random() > mutation_rate else 1 - gene for gene in chromosome)

mutation_rate = 0.01

Ending

In summary, genetic algorithms are consistent and efficient in solving optimization problems that cannot be solved directly since they imitate the evolution of species. Therefore, once you understand the basics of GAs and understand how to put them into practice in Python, solving complex tasks will become much easier. Selection, crossover, and mutation keys allow you to make modifications to solutions and consistently get the best or near-best answers. After reading this article, you will be ready to apply genetic algorithms to your own tasks and thus become better at different tasks and problem solving.

Jayita Gulati is a machine learning enthusiast and technical writer driven by her passion for building machine learning models. She has a master's degree in Computer Science from the University of Liverpool.