TREAT: A deep learning framework that achieves high-precision modeling for a wide range of dynamical systems by injecting time-reversal symmetry as inductive bias

Dynamical systems are mathematical models that explain how a system evolves due to physical interactions or forces. These systems are fundamental to understanding various phenomena in scientific fields such as physics, biology and engineering. For example, they model fluid dynamics, celestial mechanics, and robotic movements. The primary challenge in modeling these systems lies in their complexity, often involving non-linear patterns and multi-agent interactions, making it difficult to accurately predict them over long periods of time. Additionally, many systems must obey simple physical laws such as energy conservation, which further complicates the modeling process.

A persistent problem in this field is the difficulty in accurately predicting the dynamics of systems that deviate from traditional energy conservation rules. While energy-conserving systems are well understood, real-world applications often involve nonconservative systems, such as fluid dynamics or chaotic mechanical systems, that do not follow these simple rules. For example, chaotic systems like the triple pendulum are sensitive to initial conditions, causing small errors to accumulate over time, making long-term prediction a significant challenge. Inaccurate predictions in these cases can have real-world consequences, such as in engineering designs or scientific simulations where accuracy is critical.

Existing approaches to modeling these systems, such as Hamiltonian neural networks (HNN) and neural ordinary differential equations (neural ODE), attempt to improve prediction accuracy by incorporating physical priors into their models. HNNs are particularly effective for systems where energy conservation is maintained but struggle with systems that violate this principle. Other methods, such as graph neural networks (GNN) and hybrid models, focus on capturing common agent-based interactions in multi-agent systems such as robotic controls or molecular simulations. However, these methods also have limitations, especially when applied to non-conservative systems or scenarios that require long-term prediction. Models trained on limited data often fail to capture the finer details of system dynamics, leading to prediction errors.

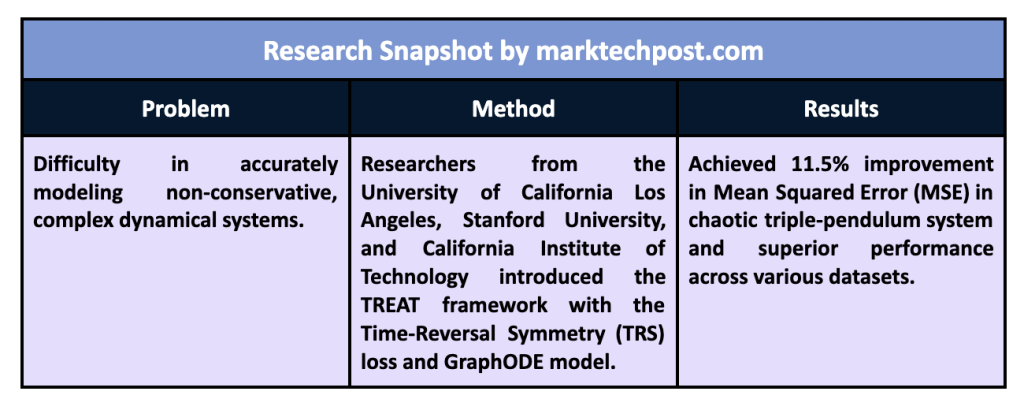
A team of researchers from the University of California, Los Angeles, Stanford University, and the California Institute of technology introduced a novel framework called TREAT (Time Reversal Symmetry ODA) to improve the accuracy of modeling dynamic systems. The TREAT framework integrates a new regularization term called Time Reversal Symmetry (TRS) loss, which ensures that the dynamics of a system remain invariant even when time is reversed. This feature is particularly important for modeling conservative and non-conservative systems, making TREAT a more flexible and robust tool for various applications. Using TRS, the model can correct errors accumulated over time, significantly improving its long-term predictive accuracy. This approach provides an overall numerical advantage for energy-conserving systems.

At the core of TREAT is the use of a GraphODE model, which predicts the forward and reverse trajectories of dynamical systems. TRS loss ensures that the model aligns these trajectories forward and backward, reducing errors and improving accuracy. This is particularly important for chaotic systems like the triple pendulum, where smaller prediction deviations can lead to drastically different results. By modeling this system, TREAT achieves a significant 11.5% reduction in mean squared error (MSE), demonstrating its effectiveness in capturing detailed dynamics that other models miss. The framework is also designed to handle multi-agent systems, where agent interactions further complicate the modeling process.

TREAT's performance has been rigorously tested on nine different data sets, spanning multiple systems, including simulated environments and real-world data. These data sets included systems with different physical properties, such as reversible and irreversible systems and single-agent and multi-agent configurations. The model outperformed state-of-the-art baselines in all cases, demonstrating its versatility and general applicability. For example, in the challenging and chaotic triple pendulum system, TREAT achieved an 11.5% improvement in prediction accuracy. Furthermore, in multi-agent systems such as the 5-body spring system, TREAT demonstrated superior performance to models such as LatentODE and TRS-ODEN, reducing the MSE to as low as 0.5400 in certain configurations.

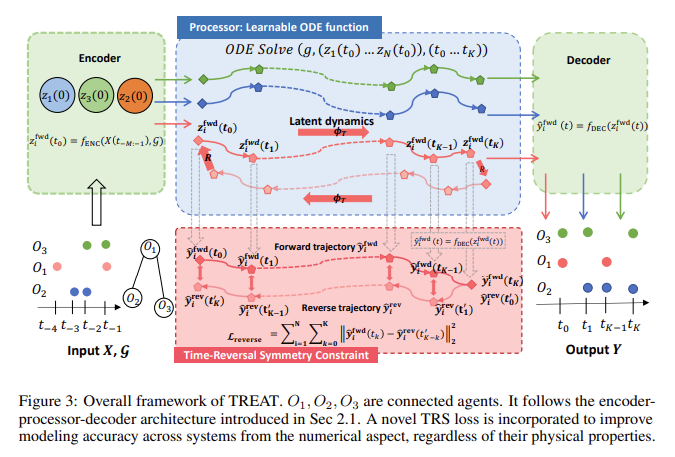
One of the key innovations of TREAT is its ability to adapt to different types of systems by adjusting the weight of the TRS regularization term. This flexibility allows the model to balance the physical limitations imposed by the loss of TRS with the need for accurate long-term predictions. In cases where the system behavior is very chaotic or non-conservative, increasing the TRS loss weight can lead to better performance. Conversely, for simpler systems, a lower weight may be more appropriate. This adaptability makes TREAT a valuable tool for various scientific and engineering applications, from modeling molecular interactions to simulating large-scale physical systems.

Key research findings:

• TREAT introduces a new time reversal symmetry (TRS) loss that improves long-term prediction accuracy.
• Achieved an 11.5% reduction in mean square error (MSE) in the chaotic triple pendulum system.
• It outperforms current models such as LatentODE and TRS-ODEN, particularly in multi-agent systems.
• The model is adaptable to conservative and non-conservative systems, making it versatile for various applications.
• It was tested on nine different data sets, demonstrating its robustness in simulated and real-world environments.

In conclusion, TREAT addresses the critical problem of accurately modeling complex and non-conservative dynamical systems by introducing time-reversal symmetry as a guiding principle. This innovative approach allows the model to correct errors in long-term predictions, significantly improving accuracy in chaotic and multi-agent systems. TREAT's success on various data sets, including simulated and real-world environments, highlights its potential as a versatile tool for researchers and engineers. TREAT can achieve state-of-the-art performance by taking advantage of TRS loss and setting a new benchmark in dynamical system modeling.

look at the Paper, GitHuband Project page. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. If you like our work, you will love our information sheet.. Don't forget to join our SubReddit over 50,000ml.

(Next live webinar: October 29, 2024) Best platform to deliver optimized models: Predibase inference engine (promoted)

Sana Hassan, a consulting intern at Marktechpost and a dual degree student at IIT Madras, is passionate about applying technology and artificial intelligence to address real-world challenges. With a strong interest in solving practical problems, he brings a new perspective to the intersection of ai and real-life solutions.