This AI article presents Find+Replace Transformers: a family of multi-transformer architectures that can probably do things that no transformer can do alone and that outperform GPT-4 in several tasks

In the annals of computing history, the journey from early mechanical calculators to Turing Complete machines has been revolutionary. While impressive, early computing devices, such as Babbage's Difference Engine and the Harvard Mark I, lacked Turing completeness, a concept that defines systems capable of performing any calculation imaginable given adequate time and resources. This limitation was not just theoretical; he delineated the boundary between simple automated calculators and full computers capable of executing any calculation task. Turing Complete systems, as conceptualized by Alan Turing and others, brought about a paradigm shift, enabling the development of complex, versatile, and composable software.

Fast forward to the present, and the field of natural language processing (NLP) has been dominated by transformative models, renowned for their ability to understand and generate human language. However, a lingering question has been its ability to achieve Turing completeness. Specifically, could these sophisticated models, fundamental to large language models (LLMs), replicate the unlimited computational potential of Turing Complete systems?

This article aims to address this question by examining the computational limits of transformer architecture and proposing an innovative path to transcend these limits. The central claim is that while individual transformer models, as currently designed, do not reach Turing completeness, a collaborative multi-transformer system could cross this threshold.

The exploration begins with a dissection of computational complexity, a framework that categorizes problems based on the resources required to solve them. It is a critical analysis since it exposes the limitations of models confined to classes of lower complexity: they cannot be generalized beyond a certain scope of problems. This is vividly illustrated by the example of lookup tables, simple but fundamentally limited in their problem-solving capabilities.

Going deeper, the article highlights how transformers, despite their advanced capabilities, encounter a limit in their computational expressiveness. This is exemplified in his struggle with problems that exceed the REGULAR class within the Chomsky Hierarchy: a classification of language types based on their grammatical complexity. These challenges underscore the inherent limitations of transformers when faced with tasks that demand a degree of computational flexibility that they inherently lack.

However, the narrative takes a turn with the introduction of the Search+Replace transformer model. This novel architecture reimagines the role of the transformer not as a solitary solver but as part of a dynamic duo (or more accurately, a team) where each member specializes in identifying (Search) or transforming (Replace) segments of data. This collaborative approach not only avoids the computational bottlenecks faced by independent models, but also closely aligns with the principles of Turing Completeness.

The elegance of the Find+Replace model lies in its simplicity and profound implications. By mirroring the reduction processes found in the lambda calculus (a system fundamental to functional programming and Turing Complete in nature), the model demonstrates unlimited computing power. This is an important advance, suggesting that transformers, when organized into a multi-agent system, can simulate any Turing machine, thus achieving Turing completeness.

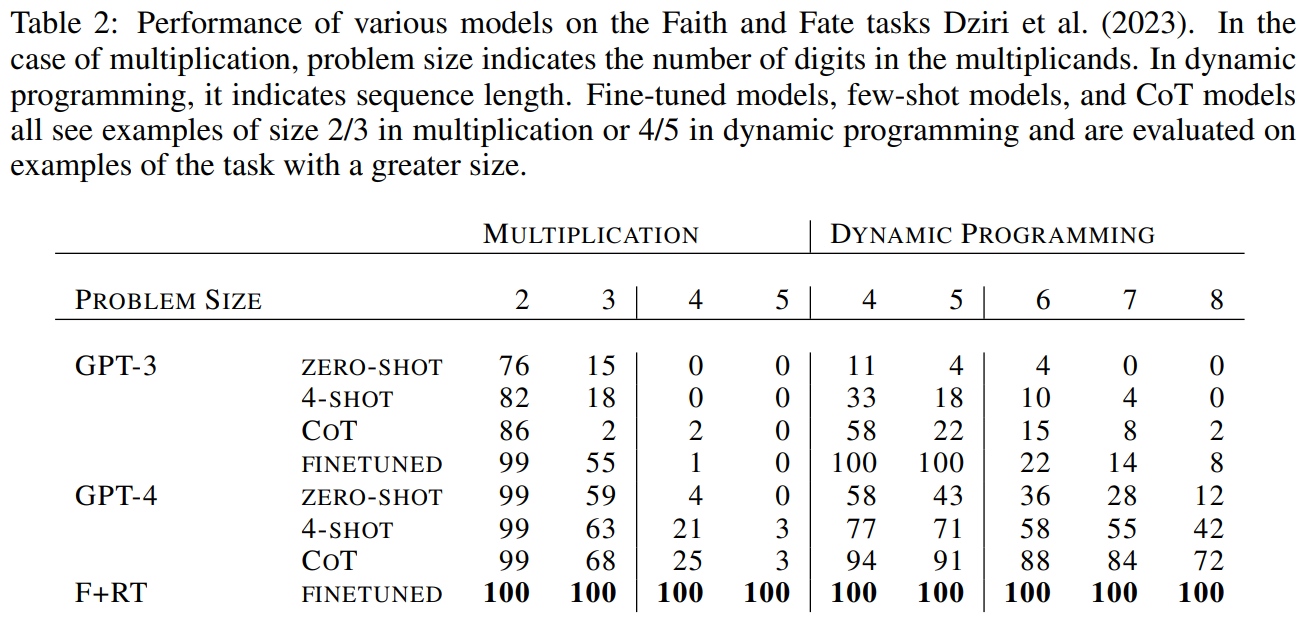
Empirical evidence reinforces this theoretical advance. Through rigorous testing, including challenges like the Tower of Hanoi and the FAITH and DESTINY tasks, Find+Replace transformers consistently outperformed their single-transformer counterparts (e.g., GPT-3, GPT-3.5, and GPT-4) . This results (shown in Table 1 and Table 2) validate the theoretical foundations of the model and show its practical superiority in addressing complex reasoning tasks that have traditionally prevented state-of-the-art transformers.

In conclusion, the finding that traditional transformers are not Turing complete highlights their potential limitations. This work establishes Find+Replace transformers as a powerful alternative, pushing the boundaries of computational power within language models. Achieving Turing completeness lays the foundation for ai agents designed to execute broader computational tasks, making them adaptable to solve increasingly diverse problems.

This work calls for continued exploration of innovative multi-transformer systems. In the future, more efficient versions of these models may offer a paradigm shift beyond the limitations of a single transformer. Turing-complete transformer architectures unlock enormous potential, paving the way to new frontiers in ai.

Review the Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on Twitter and Google news. Join our 36k+ ML SubReddit, 41k+ Facebook community, Discord Channeland LinkedIn Grabove.

If you like our work, you will love our Newsletter..

Don't forget to join our Telegram channel

<!– ai CONTENT END 2 –>