Formal mathematical reasoning represents an important frontier in artificial intelligence, addressing fundamental logic, computation, and problem-solving challenges. This field focuses on enabling machines to handle abstract mathematical reasoning with precision and rigor, expanding the applications of ai in science, engineering, and other quantitative domains. Unlike natural language processing or vision-based ai, this area uniquely combines structured logic with the creative elements of human reasoning, promising transformative advances.
Despite advances in the application of ai to mathematics, significant challenges remain in addressing complex and abstract problems. Many ai models excel at solving high school-level mathematical problems, but struggle with advanced tasks such as theorem proving and abstract logical deductions. These challenges are compounded by the scarcity of data in advanced mathematics and the inherent difficulty of verifying complex logical reasoning. This has created a critical need for new approaches to close these gaps.
Current methods in mathematical ai rely heavily on natural language processing to train large language models (LLMs) on informal data sets. These data sets include problems with step-by-step solutions derived from sources such as academic articles and online forums. While these approaches have led to successes on standardized benchmarks, they remain limited in addressing abstract and higher-level problems. Informal approaches often lead to errors in reasoning and are limited by the availability of quality data, underscoring the limitations of relying solely on these methods.
Researchers from Meta FAIR, Stanford University, UC Berkeley, the University of Edinburgh and UT Austin have introduced formal mathematical reasoning as an innovative solution. This approach uses formal systems such as Lean, Coq, and Isabelle to validate mathematical reasoning. These systems enable rigorous verification of theorems and proofs, reducing errors and providing feedback to improve ai capabilities. By grounding reasoning in formal logic, these methods create a robust framework for addressing abstract mathematical challenges while also addressing issues of data sparsity and correctness verification.
Formal reasoning uses proof assistants to ensure the soundness of mathematical proofs. The methodology combines auto-formalization (translating informal mathematics into formal syntax) with reinforcement learning to iteratively improve models. For example, Lean, a widely used testing assistant, allows researchers to validate logical tests using type checking. The process involves breaking down complex problems into smaller, verifiable subgoals. Researchers also use synthetic data generation, creating extensive data sets from fundamental axioms to train and refine ai models. These advances have allowed the integration of formal verification techniques into advanced mathematical reasoning systems, significantly improving their precision and robustness.
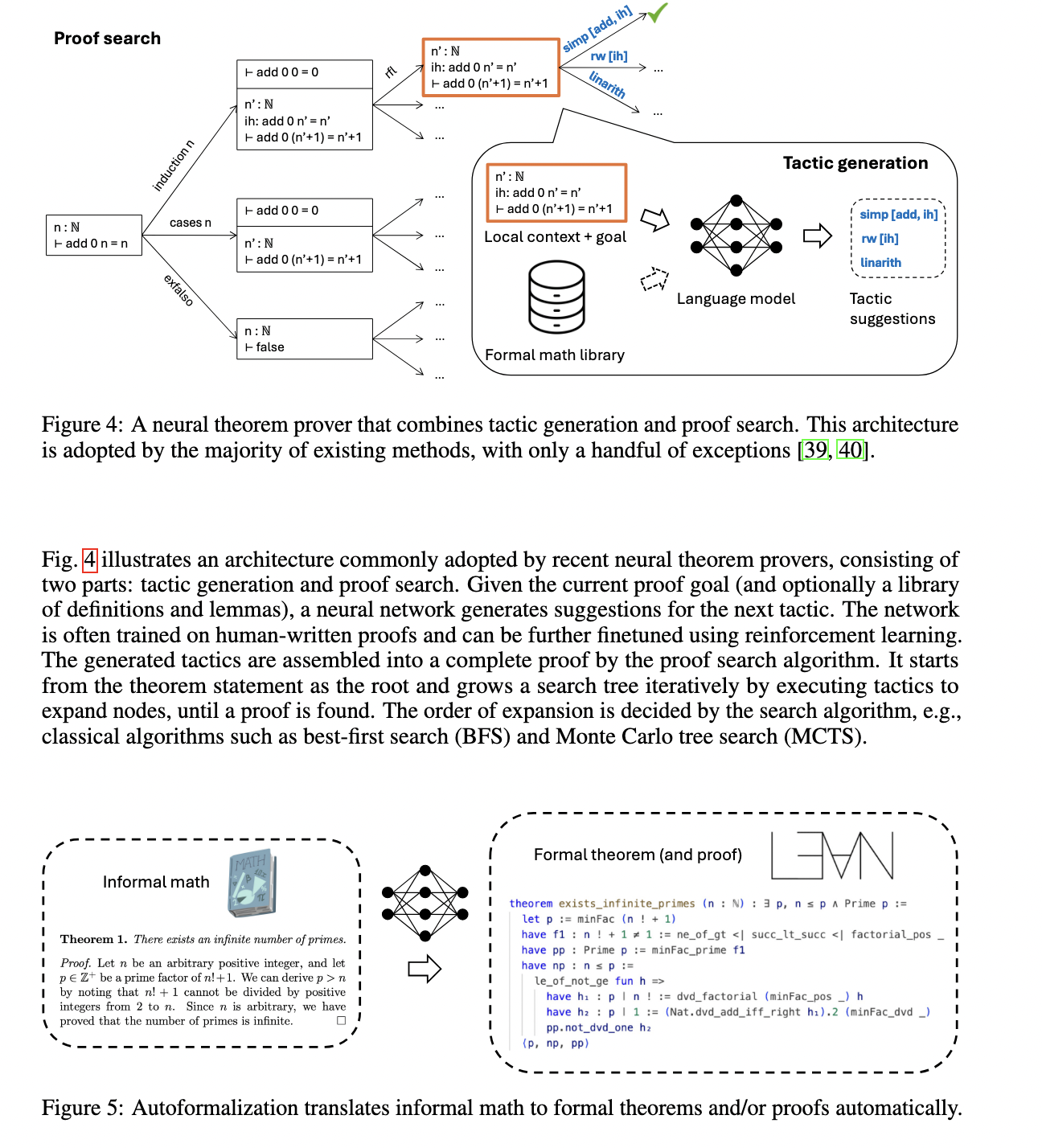
Formal reasoning systems have generated notable improvements in performance. AlphaProof achieved silver medal-level performance at the International Mathematics Olympiad (IMO) by leveraging formal methods and synthetic data. He formalized more than one million IMO-like problems, generating one hundred million formal theorems and their corresponding proofs through iterative refinement. Similarly, AlphaGeometry successfully solved complex geometry problems by combining domain-specific systems with symbolic representations. These achievements highlight the ability of formal reasoning to address abstract challenges, precisely surpassing traditional informal methods. In particular, the systems demonstrated superior performance in theorem proving, achieving success rates comparable to experienced human mathematicians in certain domains.
The integration of formal reasoning and artificial intelligence is essential to advance mathematical discovery. Researchers are paving the way for artificial intelligence systems capable of solving increasingly complex mathematical problems by addressing critical challenges such as data scarcity and logical verification. Efforts led by institutions like Meta FAIR and its collaborators underscore the transformative potential of combining formal rigor with cutting-edge artificial intelligence methodologies. This approach enhances the capabilities of ai in mathematics and lays the foundation for future innovations in various scientific and engineering disciplines.
Verify he Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on <a target="_blank" href="https://twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. Don't forget to join our SubReddit over 60,000 ml.
Trending: LG ai Research launches EXAONE 3.5 – three frontier-level bilingual open-source ai models that deliver unmatched instruction following and broad context understanding for global leadership in generative ai excellence….
Nikhil is an internal consultant at Marktechpost. He is pursuing an integrated double degree in Materials at the Indian Institute of technology Kharagpur. Nikhil is an ai/ML enthusiast who is always researching applications in fields like biomaterials and biomedical science. With a strong background in materials science, he is exploring new advances and creating opportunities to contribute.
<script async src="//platform.twitter.com/widgets.js” charset=”utf-8″>
 NEWSLETTER
NEWSLETTER





