The Creative Potential of Normalizing Flows in Generative AI

Introduction

Generative AI, with its remarkable ability to create data that closely resembles real-world examples, has garnered significant attention in recent years. While models like GANs and VAEs have stolen the limelight, a lesser-known gem called “Normalizing Flows” in generative AI has quietly reshaped the generative modeling landscape.

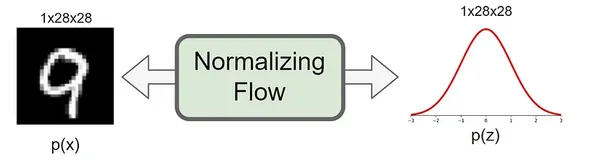
In this article, we embark on a journey into Normalizing Flows, exploring their unique features and applications and providing hands-on Python examples to demystify their inner workings. In this article, we will learn about:

• Basic understanding of Normalizing Flows.
• Applications of Normalizing Flows, such as Density estimation, Data Generation, Variational Inference, and Data Augmentation.
• Python Code example to understand Normalizing flows.
• Understanding the Affine Transformation Class.

This article was published as a part of the Data Science Blogathon.

Unmasking Normalizing Flows

Normalizing Flows, often abbreviated as NFs, are generative models that tackle the challenge of sampling from complex probability distributions. They are rooted in the concept of change of variables from probability theory. The fundamental idea is to start with a simple probability distribution, such as a Gaussian, and apply a series of invertible transformations to transform it into the desired complex distribution gradually.

The key distinguishing feature of Normalizing Flows is their invertibility. Every transformation applied to the data can be reversed, ensuring that both sampling and density estimation are feasible. This property sets them apart from many other generative models.

Anatomy of a Normalizing Flow

• Base Distribution: A simple probability distribution (e.g., Gaussian) from which sampling begins.
• Transformations: A series of bijective (invertible) transformations that progressively modify the base distribution.
• Inverse Transformations: Every transformation has an inverse, allowing for data generation and likelihood estimation.
• Final Complex Distribution: The composition of transformations leads to a complex distribution that closely matches the target data distribution.

Applications of Normalizing Flows

1. Density Estimation: Normalizing Flows excel at density estimation. They can accurately model complex data distributions, making them valuable for anomaly detection and uncertainty estimation.
2. Data Generation: NFs can generate data samples that resemble real data closely. This ability is crucial in applications like image generation, text generation, and music composition.
3. Variational Inference: Normalizing Flows plays a vital role in Bayesian machine learning, particularly in Variational Autoencoders (VAEs). They enable more flexible and expressive posterior approximations.
4. Data Augmentation: NFs can augment datasets by generating synthetic samples, useful when data is scarce.

Let’s Dive into Python: Implementing a Normalizing Flow

We implement a simple 1D Normalizing Flow using Python and the PyTorch library. In this example, we’ll focus on transforming a Gaussian distribution into a more complex distribution.

import torch
import torch.nn as nn
import torch.optim as optim

# Define a bijective transformation
class AffineTransformation(nn.Module):
    def __init__(self):
        super(AffineTransformation, self).__init__()
        self.scale = nn.Parameter(torch.Tensor(1))
        self.shift = nn.Parameter(torch.Tensor(1))
    
    def forward(self, x):
        return self.scale * x + self.shift, torch.log(self.scale)

# Create a sequence of transformations
transformations = [AffineTransformation() for _ in range(5)]
flow = nn.Sequential(*transformations)

# Define the base distribution (Gaussian)
base_distribution = torch.distributions.Normal(0, 1)

# Sample from the complex distribution
samples = flow(base_distribution.sample((1000,))).squeeze()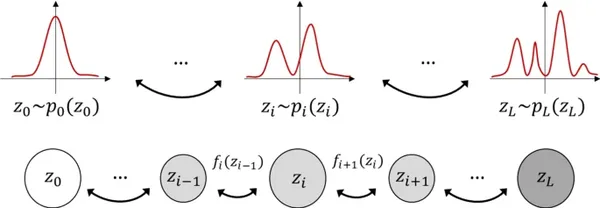

Libraries Used

1. torch: This library is PyTorch, a popular deep-learning framework. It provides tools and modules for building and training neural networks. In the code, we use it to define neural network modules, create tensors, and efficiently perform various mathematical operations on tensors.
2. torch.nn: This submodule of PyTorch contains classes and functions for building neural networks. In the code, we use it to define the nn.Module class serves as the base class for custom neural network modules.
3. torch.optim: This submodule of PyTorch provides optimization algorithms commonly used for training neural networks. In the code, it’s used to define an optimizer for training the parameters of the AffineTransformation module. However, the code I provided doesn’t explicitly include the optimizer setup.

AffineTransformation Class

The AffineTransformation class is a custom PyTorch module representing one step in the sequence of transformations used in a Normalizing Flow. Let’s break down its components:

• nn.Module: This class is the base class for all custom neural network modules in PyTorch. By inheriting from nn.Module, AffineTransformation becomes a PyTorch module itself, and it can contain learnable parameters (like self.scale and self.shift) and define a forward pass operation.
• __init__(self): The class’s constructor method. When an instance of AffineTransformation is created, it initializes two learnable parameters: self.scale and self.shift. These parameters will be optimized during training.
• self.scale and self.shift: These are PyTorch nn.Parameter objects. Parameters are tensors automatically tracked by PyTorch’s autograd system, making them suitable for optimization. Here, self.scale and self.shift represents the scaling and shifting factors applied to the input x.
• forward(self, x): This method defines the forward pass of the module. When you pass an input tensor x to an instance of AffineTransformation, it computes the transformation using the affine operation self.scale * x + self.shift. Additionally, it returns the logarithm of self.scale. The logarithm is used because it ensures that self.scale remains positive, which is important for invertibility in Normalizing Flows.

In a Normalizing Flow in a Generative AI context, this AffineTransformation class represents a simple invertible transformation applied to the data. Each step in the flow consists of such transformations, which collectively reshape the probability distribution from a simple one (e.g., Gaussian) to a more complex one that closely matches the target distribution of the data. These transformations, when composed, allow for flexible density estimation and data generation.

# Create a sequence of transformations
transformations = [AffineTransformation() for _ in range(5)]
flow = nn.Sequential(*transformations)

In the above code section, we’re creating a sequence of transformations using the AffineTransformation class. This sequence represents the series of invertible transformations that will be applied to our base distribution to make it more complex.

What’s Happening?

Here’s what’s happening:

• We’re initializing an empty list called transformations.
• We use a list comprehension to create a sequence of AffineTransformation instances. The [AffineTransformation() for _ in range(5)] construct creates a list containing five instances of the AffineTransformation class. Apply these transformations in sequence to our data.

# Define the base distribution (Gaussian)
base_distribution = torch.distributions.Normal(0, 1)

Here, we’re defining a base distribution as our starting point. In this case, we’re using a Gaussian distribution with a mean of 0 and a standard deviation of 1 (i.e., a standard normal distribution). This distribution represents the simple probability distribution from which we’ll start our sequence of transformations.

# Sample from the complex distribution
samples = flow(base_distribution.sample((1000,))).squeeze()

This section involves sampling data from the complex distribution that results from applying our sequence of transformations to the base distribution. Here’s the breakdown:

• base_distribution.sample((1000,)): We use the sample method of the base_distribution object to generate 1000 samples from the base distribution. The sequence of transformations will transform these samples to create complex data.
• flow(…): The flow object represents the sequence of transformations we created earlier. We apply these transformations in sequence by passing the samples from the base distribution through the flow.
• squeeze(): This removes any unnecessary dimensions from the generated samples. People often use it when dealing with PyTorch tensors to ensure that the shape matches the desired format.

Conclusion

NFs are generative models that sculpt complex data distributions by progressively transforming a simple base distribution through a series of invertible operations. The article explores the core components of NFs, including base distributions, bijective transformations, and the invertibility that underpins their power. It highlights their pivotal role in density estimation, data generation, variational inference, and data augmentation.

Key Takeaways

The key takeaways from the article are:

1. Normalizing Flows are generative models that transform a simple base distribution into a complex target distribution through a series of invertible transformations.
2. They find applications in density estimation, data generation, variational inference, and data augmentation.
3. Normalizing Flows offer flexibility and interpretability, making them a powerful tool for capturing complex data distributions.
4. Implementing a Normalizing Flow involves defining bijective transformations and sequentially composing them.
5. Exploring Normalizing Flows unveils a versatile approach to generative modeling, offering new possibilities for creativity and understanding complex data distributions.

Frequently Asked Questions

The media shown in this article is not owned by Analytics Vidhya and is used at the Author’s discretion.

Related