Quantized Eigenvector Matrices for 4-bit Second-Order Optimization of Deep Neural Networks

Deep neural networks (DNNs) have achieved notable success in several fields, including computer vision, natural language processing, and speech recognition. This success is largely attributed to first-order optimizers such as stochastic gradient descent with boosting (SGDM) and AdamW. However, these methods face challenges in training large-scale models efficiently. Second-order optimizers, such as K-FAC, Shampoo, AdaBK, and Sophia, demonstrate superior convergence properties, but often incur significant computational and memory costs, hindering their widespread adoption for training large models with limited memory budgets. .

Two main approaches have been explored to reduce the memory consumption of optimizer states: factorization and quantization. Factorization uses a low-rank approximation to represent optimizer states, a strategy that applies to both first-order and second-order optimizers. In a different line of work, quantization techniques use low-bit representations to compress 32-bit optimizer states. While quantization has been successfully applied to first-order optimizers, adapting it to second-order optimizers poses a greater challenge due to the matrix operations involved in these methods.

Researchers from Beijing Normal University and Singapore Management University present the first 4-bit second order optimizer, taking Shampoo as an example, maintaining comparable performance to its 32-bit counterpart. The key contribution is to quantize the eigenvector matrix of the preconditioner in 4-bit Shampoo instead of directly quantizing the preconditioner itself. This approach preserves the small singular values ​​of the preconditioner, which are crucial for accurately computing the inverse fourth root, thus avoiding performance degradation. Furthermore, computing the inverse fourth root from the quantized eigenvector matrix is ​​straightforward, ensuring no increase in wall clock time. Two techniques are proposed to improve performance: Björck orthonormalization rectify the orthogonality of the quantized eigenvector matrix, and linear square quantization overcoming dynamic tree quantization for second-order optimizing states.

The key idea is to quantize the eigenvector matrix U of the preconditioner A=UΛUT using a quantifier Q, rather than quantizing A directly. This preserves the singular value matrix Λ, which is crucial for accurately computing the power of the matrix A^(-1/4) using matrix decompositions such as SVD. Björck orthonormalization is applied to rectify the loss of orthogonality in the quantized eigenvectors. Linear square quantization is used instead of dynamic tree quantization to obtain better performance from 4-bit quantization. The preconditioner update uses the quantized eigenvectors V and the unquantized singular values ​​Λ to approximate A≈VΛVT. The inverse fourth root A^(-1/4) is approximated by quantizing it to obtain its quantized eigenvectors and reconstructing using the quantized eigenvectors and diagonal entries. Greater orthogonalization allows for accurate calculation of matrix powers. As for arbitrary s.

By conducting extensive experimentation, the researchers demonstrate the superiority of the proposed 4-bit Shampoo over first-order optimizers such as AdamW. While first-order methods require running 1.2 to 1.5 times more epochs, resulting in longer wall clock times, they still achieve lower test accuracies compared to second-order optimizers. . In contrast, 4-bit Shampoo achieves comparable test accuracies to its 32-bit counterpart, with differences ranging from -0.7% to 0.5%. Wall clock time increases for 4-bit Shampoo range from -0.2% to 9.5% compared to 32-bit Shampoo, while providing memory savings of 4.5% to 41%. %. Surprisingly, Shampoo 4-bit memory costs are only 0.8% to 12.7% higher than first-order optimizers, marking a significant advance in allowing the use of second-order methods. order.

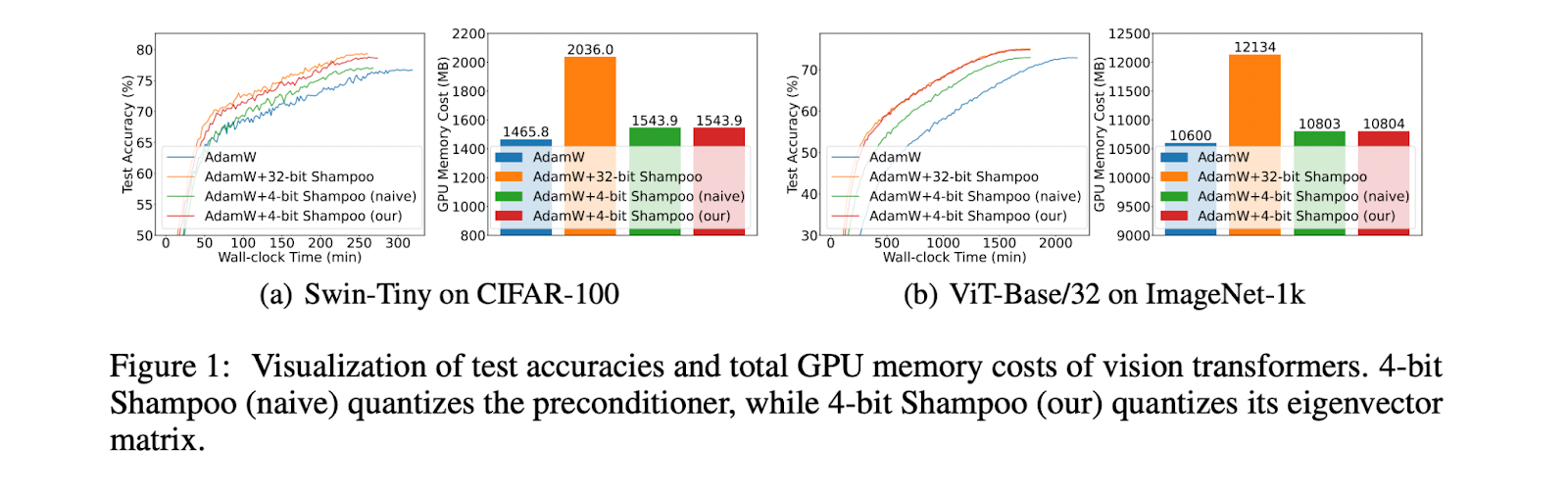
This research presents the 4 bit shampoo, designed for memory-efficient DNN training. A key finding is that quantizing the eigenvector matrix of the preconditioner, rather than the preconditioner itself, is crucial to minimizing quantization errors in your inverse fourth root calculation to 4-bit precision. This is due to the sensitivity of small singular values, which are preserved by quantizing only the eigenvectors. To further improve the performance, linear square quantization and orthogonal rectification mapping techniques are introduced. On several image classification tasks involving different DNN architectures, 4-bit Shampoo achieves performance on par with its 32-bit counterpart, while offering significant memory savings. This work paves the way to enable widespread use of memory-efficient second-order optimizers in large-scale DNN training.

Review the Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on twitter.com/Marktechpost”>twitter. Join our Telegram channel, Discord channeland LinkedIn Grabove.

If you like our work, you will love our Newsletter..

Don't forget to join our 43k+ ML SubReddit | Also, check out our ai Event Platform