In many computer applications, the system needs to make decisions to serve the requests that come online. Consider, for example, the example of a navigation application that responds to requests from drivers. In such scenarios there is inherent uncertainty about important aspects of the problem. For example, driver preferences regarding route characteristics are often unknown and delays on road sections may be uncertain. The field of online machine learning studies such scenarios and provides various techniques for decision making in problems under uncertainty.
 |
| A navigation engine has to decide how to route this user’s request. User satisfaction will depend on the (uncertain) congestion of the two routes and unknown user preferences on various characteristics, such as how scenic, safe, etc., the route is. |
A well-known problem in this framework is the Multi-armed bandit problemin which the system has a set of north available options (arms) that you are asked to choose from each round (user request), for example, a set of pre-calculated alternative routes in navigation. User satisfaction is measured by a reward that depends on unknown factors, such as user preferences and delays in road sections. The performance of an algorithm on you rounds is compared to the best set action in retrospect by means of the to regret (the difference between the reward of the best arm and the reward obtained by the algorithm over all you rounds). In it experts As a variant of the multi-armed bandit problem, all payoffs are observed after each round and not just played by the algorithm.
 |
| An example of the expert problem. The table presents the rewards obtained by following each of the 3 experts in each round = 1, 2, 3, 4. The best expert in hindsight (and therefore the benchmark for comparison) is the one in the middle, with a total reward of 21. If, for example, we had selected expert 1 in the first two rounds and expert 3 in the last two rounds (remember that we must select before looking at the rewards of each round), we would have extracted the reward 17 , which would give a regret equal to 21 – 17 = 4. |
These problems have been extensively studied and existing algorithms can achieve sublinear repentance. For example, in the multi-armed bandit problem, the best existing algorithms can achieve a regret on the order of √T. However, these algorithms focus on optimizing for worst of cases instances, and do not take into account the abundance of data available in the real world that allows us to train machine learning models capable of helping us design algorithms.
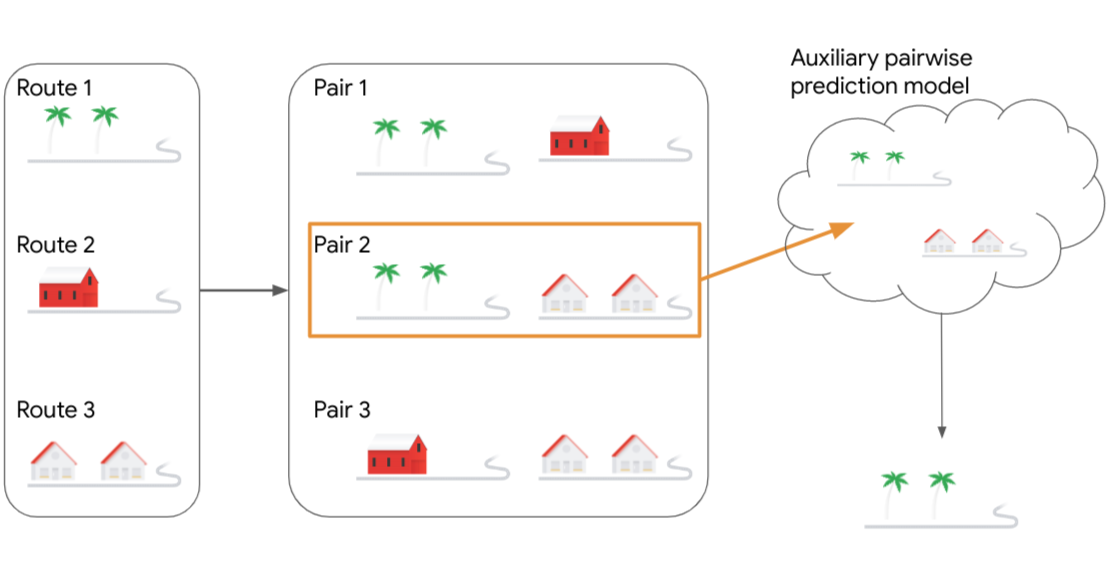
In “Online learning and bandits with consulted suggestions” (featured in ICT 2023), we show how an ML model that provides us with a weak clue can significantly improve the performance of an algorithm in a bandit-like configuration. Many ML models are accurately trained using relevant past data. In the routing app, for example, specific past data can be used to estimate delays on road segments and past driver feedback can be used to learn the quality of certain routes. Models trained on such data can, in certain cases, give very accurate feedback. However, our algorithms achieve strong guarantees even when the model’s feedback is in the form of a less explicit weak hint. Specifically, we simply ask that the model predict Which of the two options will be better? In the navigation application this is equivalent to the algorithm choosing two routes and consulting an ETA model as to which of the two is faster, or presenting the user with two routes with different characteristics and allowing them to choose the one that suits them best. By designing algorithms that take advantage of that clue, we can: Improve customer regret bandits adjustment on an exponential scale in terms of dependence on T and improve the regret of the experts configuration of the order of √T to become independent of T. Specifically, our upper bound only depends on the number of experts north y is as much log(north).
algorithmic ideas
Our algorithm for the bandits setting uses the known upper confidence limit (UCB) algorithm. The UCB algorithm keeps, as a score for each arm, the average reward observed in that arm so far and adds an optimism parameter to it that gets smaller with the number of times the arm has been pulled, thus balancing exploration and The explotion. Our algorithm applies UCB scores in pairs of armsprimarily in an effort to use the available pairwise comparison model that can designate the best of two arms. each pair of arms Yo Y j is grouped as a meta-arm (Yo, j) whose reward in each round is equal to the maximum reward between the two arms. Our algorithm looks at the UCB scores of the metaarms and chooses the pair (Yo, j) that has the highest score. The pair of arms is then passed as a query to the ML pairwise prediction helper model, which responds with the better of the two arms. This response is the arm that ultimately uses the algorithm.
 |
| The decision problem considers three candidate routes. Instead, our algorithm considers all pairs of the candidate paths. Suppose that pair 2 is the one with the highest score in the current round. The pair is delivered to the ML pairwise prediction helper model, which generates the best path of the two in the current round. |
Our algorithm for the experts fit takes a follow the regularized leader (FtRL) approach, which keeps each expert’s total reward and adds random noise to each one, before choosing the best one for the current round. Our algorithm repeats this process twice, extracting random noise twice and choosing the expert with the highest reward in each of the two iterations. The two selected experts are then used to query the ML auxiliary model. The answer of the best model between the two experts is the one played by the algorithm.
Results
Our algorithms use the concept of weak clues to achieve strong improvements in terms of theoretical guarantees, including an exponential improvement in the regret dependency on the time horizon or even removing this dependency altogether. To illustrate how the algorithm can outperform existing benchmark solutions, we present a configuration where 1 of the north candidate arms is consistently marginally better than the north-1 arms remaining. We compare our ML polling algorithm against a baseline that uses the standard UCB algorithm to choose the two arms to send to the pairwise comparison model. We observe that the UCB baseline continues to accumulate regret while the probing algorithm quickly identifies the best arm and continues to play, without accruing regret.
 |
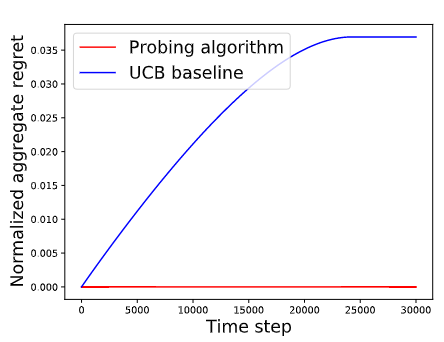| An example where our algorithm beats a UCB-based baseline. The instance considers north arms, one of which is always marginally better than the rest north-one. |
Conclution
In this paper, we explore how a simple pairwise comparison ML model can provide simple hints that are very powerful in settings such as expert and bandit problems. In our paper, we further present how these ideas apply to more complex setups, such as online linear and convex optimization. We believe that our suggestion model can have more interesting applications in ML and combinatorial optimization problems.
Thanks
We thank our co-authors Aditya Bhaskara (University of Utah), Sungjin Im (University of California, Merced), and Kamesh Munagala (Duke University).
