Introduction to the lognormal distribution

Introduction

The lognormal distribution is a fascinating statistical concept that is commonly used to model data that exhibit right-skewed behavior. This distribution has a wide range of applications in various fields, such as biology, finance, and engineering. In this article, we will delve into the log-normal distribution, its key parameters and how to interpret them, as well as explore some practical examples to improve understanding.

General description

• A log-normal distribution models data where the natural logarithm of a variable follows a normal distribution, showing positive skewness.
• Understand the shape (σ), scale (m or eμ), and location (μ) parameters to interpret and apply the log-normal distribution.
• The log-normal distribution is connected to the normal distribution; if x is log-normal, ln(x) is usually distributed and vice versa.
• Estimate the μ σ parameters from data using techniques such as maximum likelihood estimation, which involves log transformation and calculation of the mean and standard deviation.
• The lognormal distribution is widely used in biology, finance, reliability engineering, and environmental science to model right-skewed data such as growth rates, stock prices, and time to failure.

What is a lognormal distribution?

A log-normal distribution describes the probability distribution of a random variable when its logarithm follows a normal distribution. In simpler terms, if the natural logarithm of a variable x follows a normal distribution, then x follows a log-normal distribution. This distribution is still continuous and is positively skewed, meaning it has a long right tail.

Key parameters

There are mainly three parameters:

1. Shape parameter (σ): This parameter affects the general shape of the distribution. It is also the standard deviation of the log-transformed variable.
2. Scale parameter (mo mymeter): This parameter stretches or shrinks the distribution graph.. In this distribution, the scale parameter is often called the median.
3. Location parameter (meter): This parameter determines where on the x-axis the graph is located. It is the mean of the logarithmically transformed variable.

These parameters are critical to understanding how this distribution behaves and how it can be applied to real-world data.

Also read: What is the normal distribution? A definitive guide

Probability density function

The probability density function (PDF) of a log-normal distribution is given by:

where x>0, μ is the mean of the logarithm of the variable, and p is the standard deviation of the logarithm of the variable. This formula shows that the log-normal distribution is defined only for positive values, since the logarithm is not defined for non-positive values.

Relationship with the Normal Distribution

One of the most interesting aspects is its relationship with the normal distribution. If x follows a log-normal distribution, Y = ln(x) follows a normal distribution. On the contrary, if Y follows a normal distribution, x = eY follows a log-normal distribution. This relationship allows us to use well-established methods for normal distributions to analyze log-normal data by transforming the data using logarithms.

Calculate parameters from data

We often use methods such as Maximum Likelihood Estimation (MLE) to estimate the parameters of this way of distribution from data. Here is a simplified approach to estimating μ and σ:

1. Transform data into records: Take the natural logarithm of all data points.
2. Calculate the sample mean and standard deviation of the log-transformed data: These statistics will be the estimates for μ and σ.

For example, consider a logarithmically distributed income data set. By taking the natural logarithm of each income, we can calculate the mean and standard deviation of these log-transformed values ​​to estimate μ and σ.

Practical applications

This distribution is widely used in various fields due to its ability to model skewed data. Here are some examples:

1. Biology: In biological studies, growth rates of organisms typically follow a lognormal distribution because growth rates are multiplicative rather than additive.
2. Finance: Stock prices are commonly modeled using lognormal distributions because the percentage change in prices is normally distributed.
3. Reliability engineering: The time to failure of certain products can be modeled using a log-normal distribution, especially when the failure process is multiplicative.
4. Environmental science: The size distribution of particles in aerosols or the amount of rainfall in a given period.

Calculation example

Let's consider a practical example of calculating the parameters of a log-normal distribution. Suppose we have the following income data (in thousands): 20, 22, 25, 27, 30.

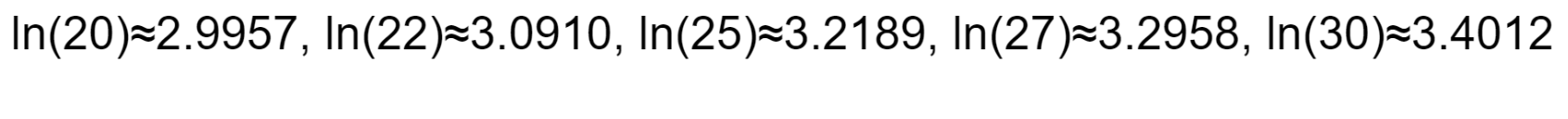
• Calculate the sample mean meter:

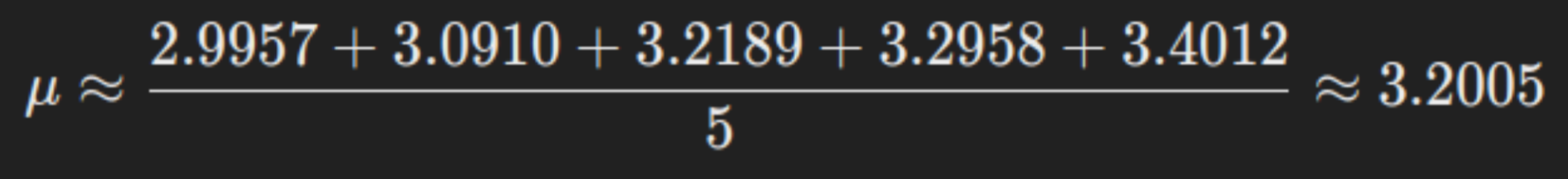
• Calculate the standard deviation of the sample (σ):

Therefore, the estimated parameters for the log-normal distribution are μ approximately 3.2005 and σ approximately 0.1504.

Interpretation of parameters

• meter: This is the mean of the log-transformed data. In our example, a μ of 3.2005 indicates that the average of the natural logarithms of income is around this value.
• in: This is the standard deviation of the log-transformed data. A σ of 0.1504 suggests that log-transformed income is relatively close to the mean on a log scale.

Conclusion

The log-normal distribution is a powerful tool for modeling right-skewed data. We can effectively analyze and interpret data in various fields by understanding its key parameters and their relationship to the normal distribution. Whether it's financial data, biological growth rates, or reliability metrics, it offers a solid framework for understanding and predicting behavior.

Frequent questions