Parallel computing continues to advance and address the demands of high-performance tasks such as deep learning, scientific simulations, and data-intensive calculations. A fundamental operation within this domain is matrix multiplication, which underpins many computational workflows. Recent hardware innovations such as Tensor Core Units (TCUs) offer efficient processing by optimizing constant-size matrix multiplications. These units are now being adapted for broader applications beyond neural networks, including graph and classification algorithms, to improve computational efficiency.
Despite these innovations, prefix addition or scan algorithms, which compute cumulative sums, still need help in matrix-based calculations. Traditional approaches should be more efficient in managing computational depth and distributing work for large data sets. Additionally, latency when initiating matrix operations and limited parallelism between tensor core units further complicate performance. Current methods based on the parallel random access machine (PRAM) model are effective for simpler binary operations, but need to exploit the full potential of modern tensor core hardware in die-intensive scenarios.
Existing methods for computing prefix sum include tree-based algorithms such as Brent-Kung, which optimize trade-offs between depth and work in the PRAM model. However, these algorithms are limited by their dependence on basic operations and are not designed for large-scale matrix calculations. GPU-based approaches using warp- and block-level algorithms have been successful with small data segments, but need help with larger data sets due to underutilization of tensor cores and high overhead of compute operations. memory as collection and dispersion.
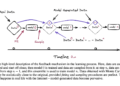
Researchers at Huawei Technologies introduced a novel algorithm called MatMulScan to address these challenges, designed specifically for the Tensor Core Unit model. The algorithm takes advantage of the capabilities of TCUs to perform efficient matrix multiplications, minimizing computational depth and achieving high performance. MatMulScan is designed for applications such as gradient boosting trees and parallel classification. It extends traditional algorithms for handling matrices, using specialized designs such as lower triangular matrices to encode local prefix additions and scalar vector additions.
MatMulScan consists of two main phases: an upscan phase and a downscan phase. During the upsweep phase, prefix sums are calculated to increase the indices, ensuring efficient calculation of cumulative sums for subsets of data. The sweep-down phase propagates these prefix sums through the remaining data, correcting any local sums to produce accurate results. This approach optimizes latency and hardware utilization, ensuring scalability for large data sets. The analysis shows that the algorithm achieves significant reductions in computational depth and performs efficiently on large-scale matrix operations.
Extensive evaluations of MatMulScan demonstrated its practical usefulness. For example, the algorithm effectively reduces computational depth compared to traditional methods while performing fewer matrix multiplications. Its job requirements are optimized for large data sets, making it a strong candidate for real-world applications. Additionally, the algorithm addresses latency costs by integrating efficient matrix multiplication processes with hardware-specific optimizations. This ensures linear scalability with data size, making it suitable for high-performance computing environments.
The study highlighted several key findings that contribute to the advancement of parallel computations:
- Reduced computational depth: The algorithm optimizes computational depth, significantly reducing the processing steps required for large data sets.
- Improved scalability: Scales efficiently with increasing data sizes, maintaining performance across diverse applications.
- Improved hardware utilization: By taking advantage of the capabilities of the tensor core, the algorithm improves hardware efficiency, overcoming the limitations seen in previous methods.
- Wide applicability: Beyond prefix sums, MatMulScan demonstrates potential in applications such as gradient boosting tree models, parallel classification, and graph algorithms.


In conclusion, MatMulScan is a fundamental development in parallel scanning algorithms, addressing traditional scalability and computational depth limitations. By integrating tensor core technology, the algorithm balances performance and practicality, paving the way for future advances in high-performance computing. This research expands the utility of TCUs and lays the foundation for innovative applications in computational science and engineering.
Verify he Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on <a target="_blank" href="https://twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. If you like our work, you will love our information sheet.. Don't forget to join our 59k+ ML SubReddit.
Sana Hassan, a consulting intern at Marktechpost and a dual degree student at IIT Madras, is passionate about applying technology and artificial intelligence to address real-world challenges. With a strong interest in solving practical problems, he brings a new perspective to the intersection of ai and real-life solutions.
<script async src="//platform.twitter.com/widgets.js” charset=”utf-8″>
 NEWSLETTER
NEWSLETTER