The mountain hiker analogy:
Imagine you are a mountain hiker and you find yourself somewhere on the slopes of a vast mountain range. Your goal is to reach the lowest point of the valley, but there is a problem: you are blindfolded. Without the ability to see the entire landscape, how would you find your way to the bottom?
Instinctively, you can feel the ground around you with your feet, sensing which direction you are going downhill. Then you would take a step in that direction, the steepest descent. By repeating this process, you will gradually approach the lowest point of the valley.
In the realm of machine learning, this hiker’s journey reflects the gradient descent algorithm. That is how:
1) The Landscape: The mountainous terrain represents our cost (or loss) function,
J(θ). This function measures the error or discrepancy between our model predictions and the actual data. Mathematically it could be represented as:
where
m is the number of data points, hθ (x) is the prediction of our model and
and it is the real value.
2) The Walker’s Position: Its current position on the mountain corresponds to the current values of the model parameters,θ. As you move, these values change, altering the model’s predictions.
3) Feeling the ground: Just as you feel the steepest descent with your feet, in gradient descent, we calculate the gradient,
∇J(θ). This gradient tells us the direction of the steepest increase in our cost function. To minimize the cost, we move in the opposite direction. The gradient is given by:
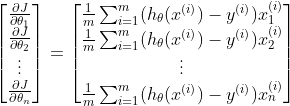
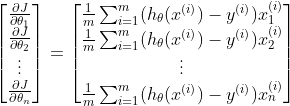
Where:
m is the number of training examples.
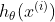
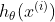is the prediction for the ith
training example.
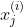
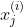is the value of feature j for training example i.
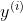
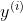is the actual output for the ith
training example.
4) Steps: The size of the steps it takes is analogous to the learning rate in gradient descent, denoted by ?. A large step might help you descend faster, but you risk overshooting the valley floor. A smaller step is more cautious, but it could take longer to reach the minimum. The update rule is:
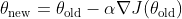
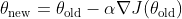
5) Get to the bottom: The iterative process continues until a point is reached where no significant decline is felt in either direction. In gradient descent, this is when the change in the cost function becomes negligible, indicating that the algorithm has (hopefully) found the minimum.
In conclusion
Gradient descent is a methodical, iterative process, much like our blindfolded hiker trying to find the lowest point in the valley. By combining intuition with mathematical rigor, we can better understand how machine learning models learn, adjust their parameters, and improve their predictions.
Batch Gradient Descent calculates the gradient using the entire data set. This method provides stable convergence and a consistent error gradient, but can be computationally expensive and slow for large data sets.
SGD estimates the gradient using a single randomly chosen data point. While it may be faster and able to escape local minima, it has a more erratic convergence pattern due to its inherent randomness, potentially leading to oscillations in the cost function.
Mini-batch gradient descent strikes a balance between the two aforementioned methods. Computes the gradient using a subset (or “mini-batch”) of the data set. This method accelerates convergence by benefiting from the computational advantages of matrix operations and offers a compromise between the stability of batch gradient descent and the speed of SGD.
Local Minimums
Gradient descent can sometimes converge to a local minimum, which is not the optimal solution for the entire function. This is particularly problematic in complex landscapes with multiple valleys. To overcome this, incorporating momentum helps the algorithm navigate through valleys without getting stuck. Additionally, advanced optimization algorithms like Adam combine the benefits of momentum and adaptive learning rates to ensure stronger convergence to global minima.
Gradients that disappear and explode
In deep neural networks, as gradients propagate back, they can decrease to almost zero (fade away) or grow exponentially (explode). Vanishing gradients slow down training, making it harder for the network to learn, while exploding gradients can cause the model to diverge. To mitigate these issues, gradient clipping sets a threshold value to prevent gradients from becoming too large. On the other hand, normalized initialization techniques, such as He or Xavier initialization, ensure that the weights are set to optimal values at the beginning, reducing the risk of these challenges.
import numpy as np
def gradient_descent(X, y, learning_rate=0.01, num_iterations=1000):
m, n = X.shape
theta = np.zeros(n) # Initialize weights/parameters
cost_history = () # To store values of the cost function over iterations
for _ in range(num_iterations):
predictions = X.dot(theta)
errors = predictions - y
gradient = (1/m) * X.T.dot(errors)
theta -= learning_rate * gradient
# Compute and store the cost for current iteration
cost = (1/(2*m)) * np.sum(errors**2)
cost_history.append(cost)
return theta, cost_history
# Example usage:
# Assuming X is your feature matrix with m samples and n features
# and y is your target vector with m samples.
# Note: You should add a bias term (column of ones) to X if you want a bias term in your model.
# Sample data
X = np.array(((1, 1), (1, 2), (1, 3), (1, 4), (1, 5)))
y = np.array((2, 4, 5, 4, 5))
theta, cost_history = gradient_descent(X, y)
print("Optimal parameters:", theta)
print("Cost history:", cost_history)This code provides a basic gradient descent algorithm for linear regression. The gradient_descent function takes the feature matrix X, the target vector y, a learning rate, and the number of iterations. Returns the optimized parameters (theta) and the history of the cost function over the iterations.
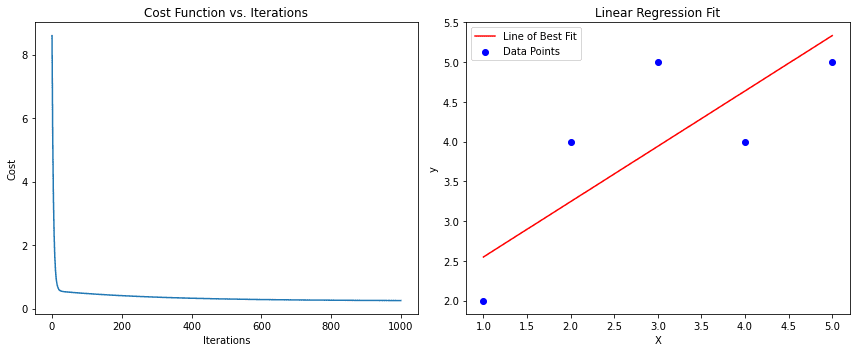
The left subplot shows the cost function decreasing with iterations.
The right subplot shows the data points and the line of best fit obtained from gradient descent.
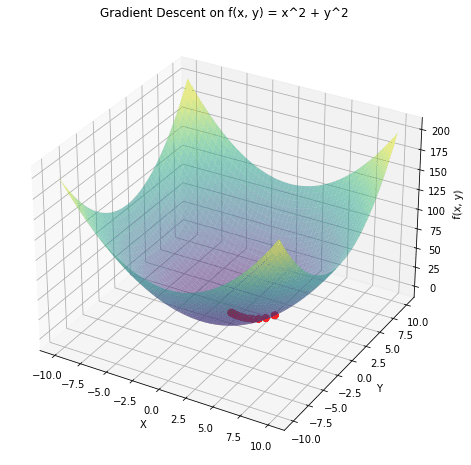
a 3D graph of the function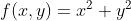 
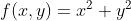and overlay in red the path taken by the gradient descent. Gradient descent starts from a random point and proceeds towards the minimum of the function.
Stock price prediction
Financial analysts use gradient descent along with algorithms such as linear regression to predict future stock prices based on historical data. By minimizing the error between predicted and actual stock prices, they can refine their models to make more accurate predictions.
Image recognition
Deep learning models, especially convolutional neural networks (CNN), employ gradient descent to optimize weights while training on large image data sets. For example, platforms like Facebook use these models to automatically tag people in photographs by recognizing facial features. The optimization of these models guarantees accurate and efficient facial recognition.
Analysis of feelings
Companies use gradient descent to train models that analyze customer comments, reviews, or social media mentions to determine public sentiment about their products or services. By minimizing the difference between predicted and actual sentiments, these models can accurately classify feedback as positive, negative, or neutral, helping businesses measure customer satisfaction and adapt their strategies accordingly.
Arun is an experienced senior data scientist with over 8 years of experience leveraging the power of data to drive impactful business solutions. He excels at leveraging advanced analytics, predictive modeling, and machine learning to transform complex data into actionable insights and strategic narratives. With a PGP in Machine Learning and artificial intelligence from a renowned institution, Arun’s experience spans a broad spectrum of technical and strategic domains, making him a valuable asset in any data-driven endeavor.
