Regression tasks, which imply predicting continuous numerical values, have traditionally been based on numerical heads such as Gaussian parameterizations or specific tensioning projections. These traditional approaches have strong distribution assumption requirements, require many data labeled and tend to decompose when modeling advanced numerical distributions. New research on large language models introduces a different approach: representing numerical values such as discrete tokens sequences and using self -giving decoding for prediction. However, this change comes with several serious challenges, including the need for an efficient tokenization mechanism, the potential for loss of numerical precision, the need to maintain stable training and the need to overcome the lack of inductive bias of token forms sequential for numeric values. Overcoming these challenges would lead to an even more powerful, efficient and flexible regression frame, thus extending the application of deep learning models beyond traditional approaches.
Traditional regression models are based on numerical tensioner projections or parametric distribution heads, such as Gaussian models. While these conventional approaches are widespread, they also have several inconveniences. Gaussian -based models have the disadvantage of assuming normally distributed exits, restricting the ability to model more advanced multimodal distributions. Punctual regression heads fight with highly non -linear or discontinuous relationships, which restricts their ability to generalize in several data sets. High dimension models, such as Riemann distributions based on histograms, are computational and intensive in data and, therefore, inefficient. In addition, many traditional approaches require explicit normalization or scale of production, introducing an additional layer of complexity and potential instability. Although conventional work has tried to use a text to text using large language models, little systematic work has been done in the regression of “anything to the text”, where numerical outputs are represented as tokens sequences, thus introducing a new paradigm for numerical prediction.
Google Deepmind researchers propose an alternative regression formulation, reformulating numerical prediction as a problem of self -giving sequence generation. Instead of generating values directly, this method encodes numbers such as Token sequences and uses a restricted decoding to generate valid numerical outputs. The coding of numerical values such as discrete token sequences makes this method more flexible and expressive when modeling real value data. Unlike Gaussian -based approaches, this method does not imply solid distribution assumptions about the data, which makes it more generalizable for real world's tasks with heterogeneous patterns. The model accommodates the precise modeling of multimodal and complex distributions, thus improving its performance in density estimation, as well as punctual regression tasks. By taking the advantages of self -representative decoders, it takes advantage of the recent language modeling progress and at the same time retains competitive performance in relation to standard numerical heads. This formulation presents a robust and flexible frame that can model a wide range of numerical relationships, offering a practical substitute for standard regression methods that are generally considered inflexible.
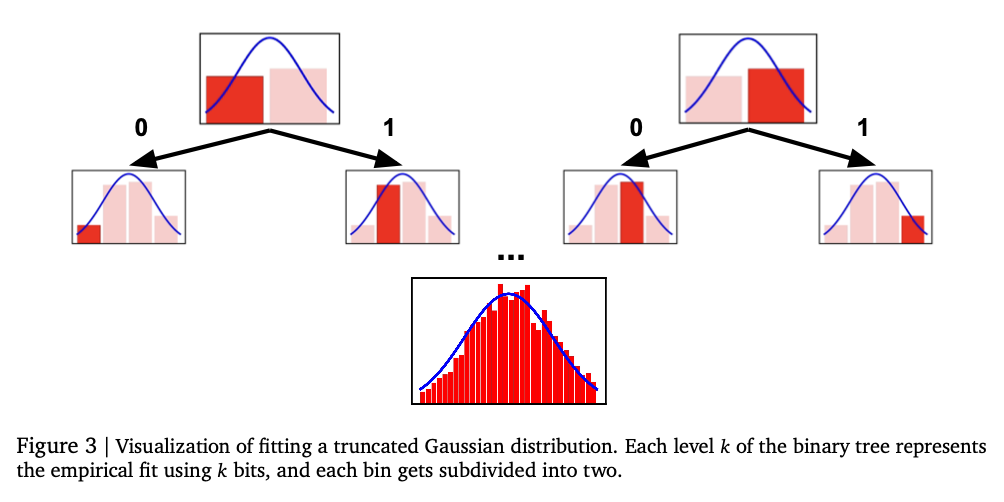
The approach uses two tokenization methods for numerical representation: standardized token and non -abnormalized token. Standardized token encodes numbers in a fixed range with base-B expansion to provide a finer precision with a growing sequence length. Non-abnormalized token extends the same idea to broader numerical ranges with a generalized floating point representation such as IEEE-754 without the need for explicit normalization. A self-spring transformer model generates token numerical outputs by Token subject to restrictions to provide valid numerical sequences. The model is trained using crossed entropy loss on the token sequence to provide precise numerical representation. Instead of predicting a scalar output directly, the system shows token sequences and uses statistical estimation techniques, such as average or medium calculation, for final prediction. The evaluations are carried out in tabular regression data sets of the real world of the OpenML-CTR23 and AMLB reference points and are compared to the Gaussian mixing models, the regression based on histograms and the standard punctual regression heads. Hyperparameter tuning is carried out in several decoders configurations, such as variations in the number of layers, hidden units and tokens vocabularies, to provide optimized performance.
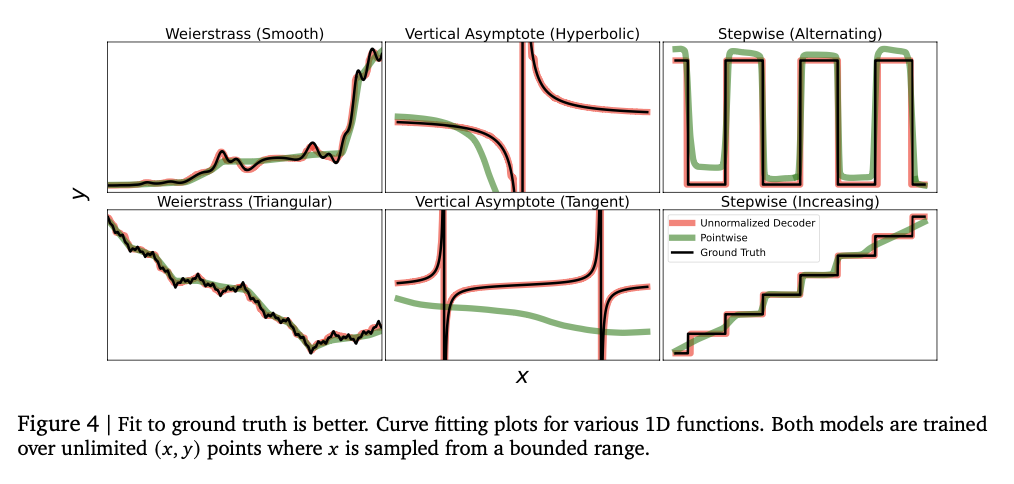
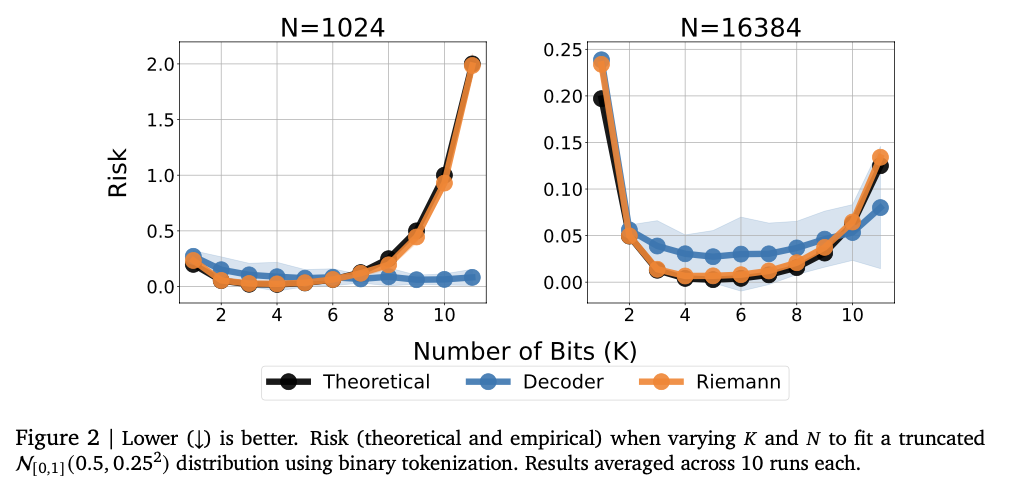
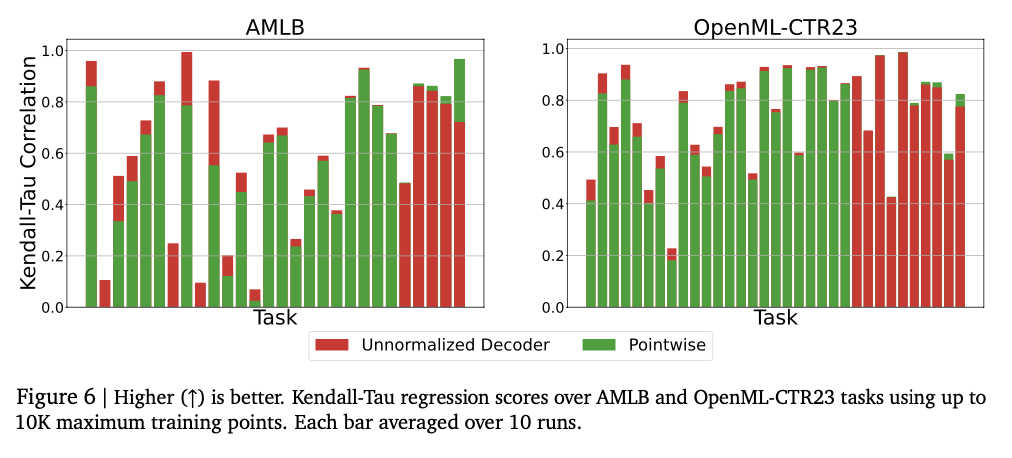
The experiments show that the model successfully captures intricate numerical relationships, achieving strong performance in a variety of regression tasks. It attends the high correlation scores of Kendall-Tau in the tabular regression, often exceeding the reference models, especially in low environments in the data where numerical stability is essential. The method is also better in density estimation, successfully capturing complex distributions and exceeding Gaussian mixing models and riemann -based approaches in negative tests of logarithmic probability. The adjustment of the size of the model at the beginning improves the performance, with an overcapacity that causes the overjuste. Numerical stability improves greatly through error correction methods such as tokens repetition and majority vote, minimizing vulnerability to atypical values. These results make this regression framework a robust and adaptive alternative to traditional methods, which shows its ability to successfully generalize in several sets of data and modeling tasks.
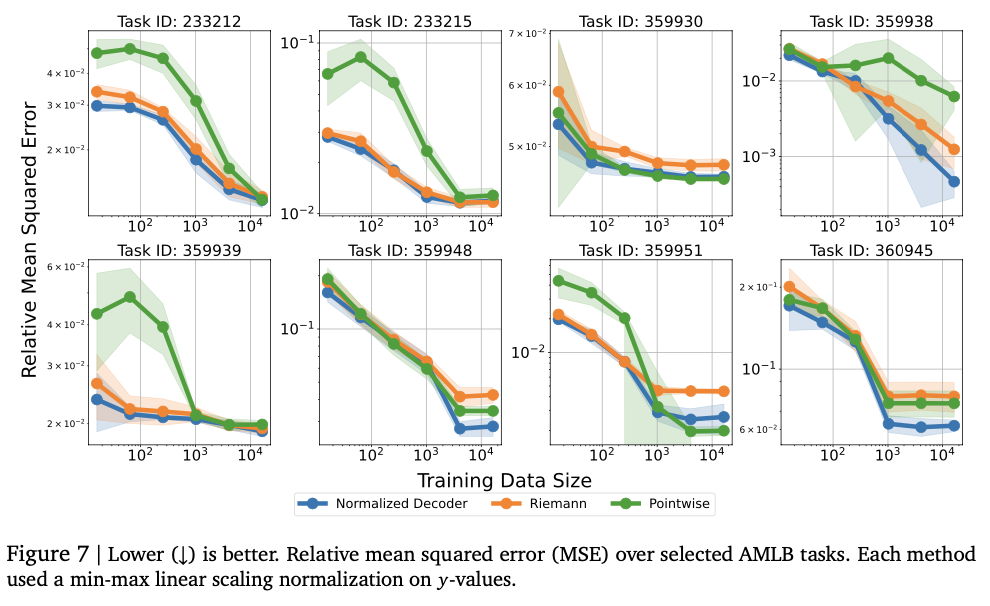
This work introduces a novel approach to numerical prediction by taking advantage of tokenized representations and automatic decoding. By replacing traditional numerical regression heads with token -based exits, the frame improves flexibility in real value data modeling. Attentive a competitive performance in various regression tasks, especially in density estimate and tabular modeling, while providing theoretical guarantees to approximate arbitrary probability distributions. Super to traditional regression methods in important contexts, especially in the modeling of complex distributions and scarce training data. Future work implies improving tokenization methods for better precision and numerical stability, extending the framework to multiple regression and high -dimension prediction tasks and investigating their applications in the modeling of reinforcement learning rewards and numerical estimate based In the vision. These results make the numerical regression based on the sequence a promising alternative to traditional methods, expanding the scope of the tasks that language models can solve successfully.
Verify he Paper and Github page. All credit for this investigation goes to the researchers of this project. Besides, don't forget to follow us <a target="_blank" href="https://x.com/intent/follow?screen_name=marktechpost” target=”_blank” rel=”noreferrer noopener”>twitter and join our Telegram channel and LINKEDIN GRsplash. Do not forget to join our 75K+ ml of submen.
Marktechpost is inviting companies/companies/artificial intelligence groups to associate for their next ai magazines in 'Open Source ai in production' and 'ai de Agent'.
Aswin AK is a consulting intern in Marktechpost. He is chasing his double title at the Indian technology Institute, Kharagpur. He is passionate about data science and automatic learning, providing a solid academic experience and a practical experience in resolving real -life dominance challenges.
 NEWSLETTER
NEWSLETTER





