Data may be viewed as having a structure in various areas that explains how its components fit together to form a greater whole. Depending on the activity, this structure is typically latent and changes. Consider Figure 1 for illustrations of distinct structures in natural language. Together, the words make up a sequence. There is a part-of-speech tag applied to each word in a sequence. These tags are interconnected, generating the red-hued linear chain. By segmenting the sentence, which is depicted with bubbles, the words in the sentence may be put together into tiny, disjointed, contiguous clusters. A more thorough examination of language would reveal that groups may be made recursively, creating a syntactic tree structure. Structures can connect two languages as well.
An alignment, for instance, in the same picture can link a Japanese translation to an English source. These grammatical constructs are universal. In biology, similar structures can be found. Tree-based models of RNA capture the hierarchical aspect of the protein folding process, whereas monotone alignment is used to match the nucleotides in RNA sequences. Genomic data is also split into contiguous groups. Most current deep-learning models make no explicit attempt to represent the intermediate structure and instead seek to predict output variables straight from the input. These models could benefit from explicit modeling of structure in several ways. Using the appropriate inductive biases could facilitate improved generalization. This would enhance downstream performance in addition to sample efficiency.
Explicit structure modeling can incorporate a problem-specific set of restrictions or methods. The judgments made by the model are also more easily understandable because of the discrete structure. Finally, there are occasions when the structure is the result of learning itself. For instance, they may be aware that the data is explained by a hidden structure of a certain shape, but they need to know more about it. For modeling sequences, auto-regressive models are the predominant technique. In some situations, non-sequential structures can be linearized and proxied by a sequential structure. These models are strong because they don’t rely on independent assumptions and can be trained using much data. While identifying the ideal structure or marginalizing over hidden variables are common inference issues, sampling from auto-regressive models is often not tractable.
Using auto-regressive models in large-scale models is challenging because they demand biassed or high-variance approximations, which are frequently computationally costly. Models over factor graphs that factorize the same way as the target structure are an alternative to auto-regressive models. These models can precisely and efficiently calculate all interesting inference issues by employing specialized methods. Although each structure requires a unique method, each inference task does not require a specialized algorithm (argmax, sampling, marginals, entropy, etc.). To extract several numbers from just one function for each structure type, SynJax employs automated differentiation, as they shall demonstrate later.
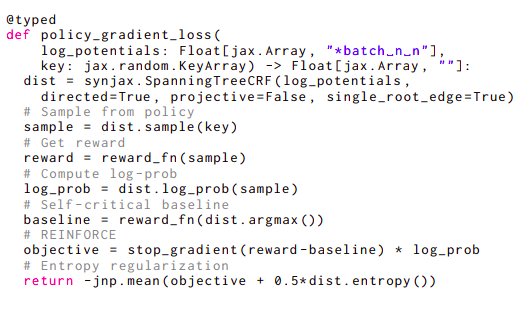
The lack of practical libraries that would offer accelerator-friendly implementations of structure components has slowed research into structured distributions for deep understanding, especially since these components depend on algorithms that frequently do not map directly onto available deep learning primitives, unlike Transformer models. Researchers from Google Deepmind offer simple-to-use structural primitives that combine within the JAX machine learning framework, helping SynJax solve the challenge. Consider the example in Figure 2 to demonstrate how simple SynJax is to use. This code implements a policy gradient loss that necessitates computing several parameters, including sampling, argmax, entropy, and log probability, each of which requires a separate approach.
The structure is a nonprojective directed spanning tree with a single root edge restriction in this code line. As a result, SynJax will employ dist.sample() Wilson’s sampling approach for single-root trees, dist.entropy (), and Tarjan’s maximum spanning tree algorithm for single-root edge trees. Single-root edge trees can use the Matrix-Tree Theorem. Only one flag needs to be changed for SynJax to use entirely different algorithms that are suitable for that structure—Kuhlmann’s algorithm for argmax and various iterations of Eisner’s algorithm for other quantities—if they only want to slightly alter the type of trees by mandating that the trees adhere to the projectivity constraint as users. Because SynJax takes care of everything related to such algorithms, the user may concentrate on the modeling aspect of their issue without implementing them or even understanding how they work.
Check out the Paper and Github. All Credit For This Research Goes To the Researchers on This Project. Also, don’t forget to join our 28k+ ML SubReddit, 40k+ Facebook Community, Discord Channel, and Email Newsletter, where we share the latest AI research news, cool AI projects, and more.
![]()
Aneesh Tickoo is a consulting intern at MarktechPost. He is currently pursuing his undergraduate degree in Data Science and Artificial Intelligence from the Indian Institute of Technology(IIT), Bhilai. He spends most of his time working on projects aimed at harnessing the power of machine learning. His research interest is image processing and is passionate about building solutions around it. He loves to connect with people and collaborate on interesting projects.
 NEWSLETTER
NEWSLETTER
 Use SQL to predict the future (Sponsored)
Use SQL to predict the future (Sponsored)




