When quantum computers were first proposed, they were expected to be a way to better understand the quantum world. With a so-called “quantum simulator”, a quantum computer could be designed to investigate how various quantum phenomena arise, including those that are intractable to simulate with a classical computer.
But making a useful quantum simulator has been challenging. Until now, quantum simulations with superconducting qubits have been used predominantly to verify pre-existing theoretical predictions and have rarely explored or discovered new phenomena. Only a few experiments with trapped ions or cold atoms have revealed new insights. Superconducting qubits, while one of the leading candidates for universal quantum computing and have demonstrated computational capabilities beyond the classical scopeso far they have not delivered their potential for discovery.
In “Formation of robust bound states of interacting photons“, published in Nature, we describe a previously unpredictable phenomenon discovered for the first time through experimental research. First, we present experimental confirmation of the theoretical prediction of the existence of a particle composed of interacting photons, or a bound stateusing the Google Sycamore Quantum Processor. Second, while studying this system, we found that although one might assume that bound states are brittle, they are still robust to perturbations that we expected would otherwise have destroyed them. This not only opens up the possibility of designing systems that take advantage of interactions between photons, but also marks a step forward in the use of superconducting quantum processors to make new scientific discoveries by simulating out-of-equilibrium quantum dynamics.
General description
photons, or how many Electromagnetic radiation such as light and microwaves usually do not interact. For example, two intersecting flashlight beams will pass through undisturbed. In many applications, such as telecommunications, weak photon interactions are a valuable feature. For other applications, such as light-based computers, the lack of interactions between photons is a drawback.
In a quantum processor, qubits house microwave photons, which can interact through two-qubit operations. This allows us to simulate the model XXZthat describes the behavior of interacting photons It is important to note that this is one of the some examples of embeddable models, that is to say. one with a high degree of symmetry, which greatly reduces its complexity. When we implemented the XXZ model on the Sycamore processor, we observed something surprising: the interactions force the photons to form packets known as bound states.
Using this well-understood model as a starting point, we then took the study to a less-understood regimen. We break the high level of symmetries shown in the XXZ model by adding additional sites that can be occupied by photons, making the system no longer integrable. While this non-integrable regime is expected to exhibit chaotic behavior in which bound states dissolve in their usual, solitary fashion, we find that they survive!
bound photons
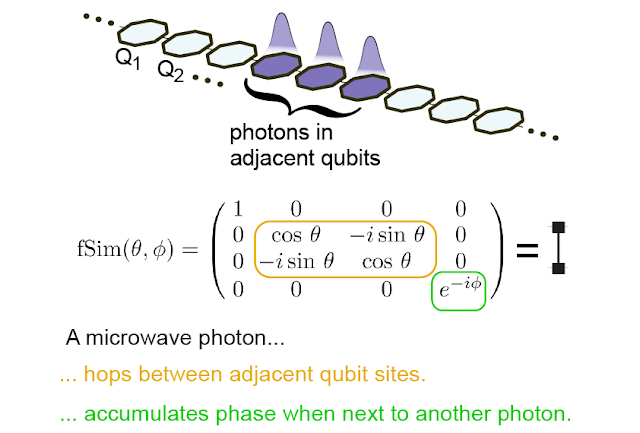
To design a system that can support the formation of bound states, we study a ring of superconducting qubits that host microwave photons. If a photon is present, the value of the qubit is “1”, and if not, the value is “0”. Through the calls Quantum gate “fSim”we connect neighboring sites, which allows photons to hop and interact with other photons at the nearest neighboring sites.
 |
| Superconducting qubits can be occupied or vacated by microwave photons. The “fSim” gate operation allows photons to jump and interact with each other. The corresponding unit evolution has a jump term between two sites (orange) and an interaction term corresponding to an added phase when two adjacent sites are occupied by a photon. |
 |
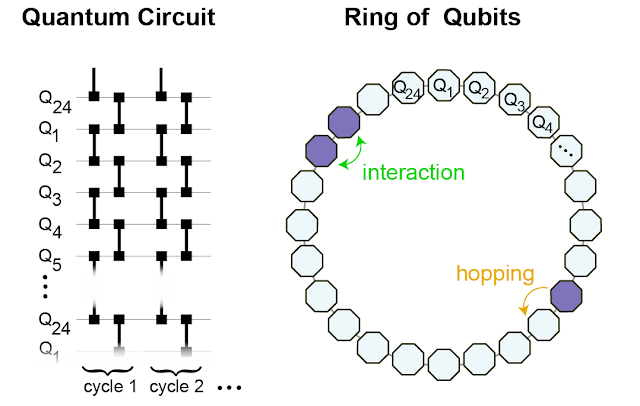| We implement the fSim gate between neighboring qubits (left) to effectively form a ring of 24 interconnected qubits in which we simulate the behavior of interacting photons (right). |
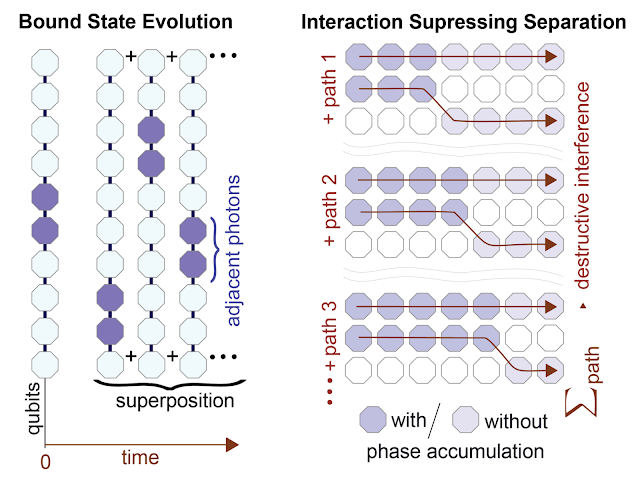
The interactions between photons affect their so-called “phase”. This phase keeps track of the oscillation of the photon’s wave function. When the photons do not interact, their phase accumulation is uninteresting. Like a well-rehearsed chorus, everyone is in sync with each other. In this case, a photon that was initially next to another photon can move away from its neighbor without losing synchronization. Just as each person in the chorus contributes to the song, all possible paths the photon can take contribute to the photon’s overall wave function. A group of photons initially clustered at neighboring sites will become a superposition of all the possible paths each photon could have taken.
When photons interact with their neighbors, this is no longer the case. If a photon moves away from its neighbor, its phase accumulation rate changes and it loses synchronization with its neighbors. All the paths in which the photons separate overlap, leading to destructive interference. It would be as if each member of the choir sang to their own beat: the song itself fades out and becomes impossible to discern through the din of the individual singers. Among all the possible configuration paths, the only possible scenario that survives is the configuration in which all photons remain bundled in a bound state. This is the reason why the interaction can be enhanced and lead to the formation of a bound state: by suppressing all other possibilities where the photons are not bound together.
 |
| Left: Evolution of photons that interact forming a bound state. Right: Time goes from left to right, each path represents one of the paths that can break the bound state of 2 photons. Due to the interactions, these paths destructively interfere, preventing the photons from being separated. |
 |
| Occupancy probability versus door cycle, or discrete time step, for north-United States to photons. We prepare linked states of different sizes and watch them evolve. We observe that most of the photons (darker colors) stick together. |
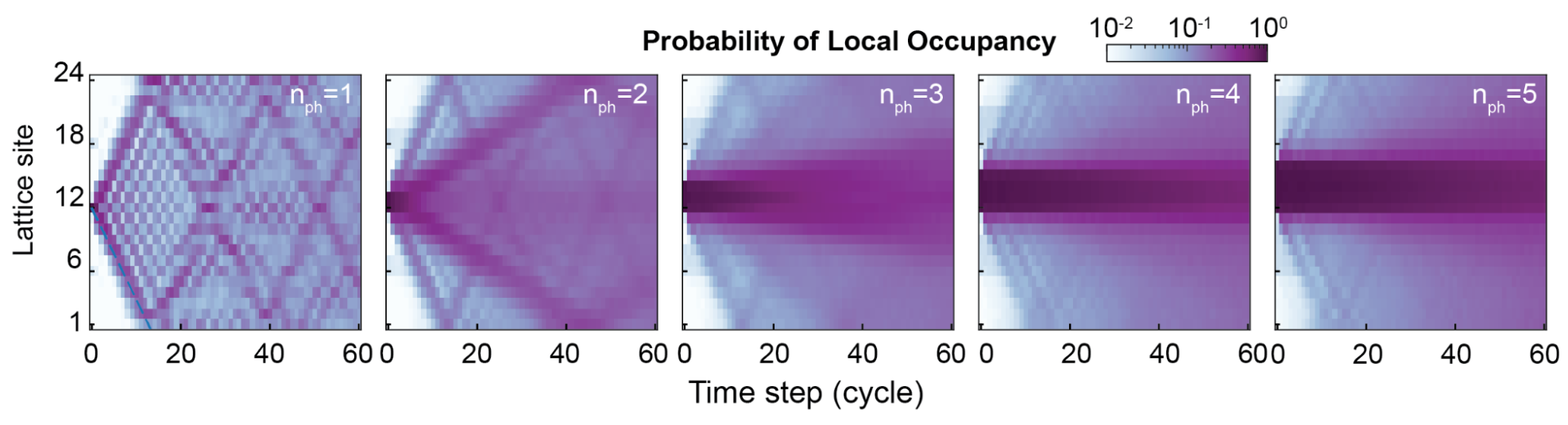
On our processor, we start by placing two to five photons at adjacent sites (that is, initializing two to five adjacent qubits to “1” and the remaining qubits to “0”) and then study how they propagate. First, we note that in the theoretically predicted regime of parameters, they stick together. Next, we find that the larger bound states move more slowly around the ring, consistent with their being “heavier”. This can be seen in the graph above, where the lattice sites closest to Site 12, the starting position of the photons, remain darker than the others as the number of photons increases (northph) in the bound state, indicating that with more bound photons there is less propagation around the ring.
Bound states behave like individual composite particles.
To show more rigorously that bound states behave like individual particles with well-defined physical properties, we devised a method to measure how the energy of particles changes with momentum, i.e., the energy-momentum. dispersion relation.
To measure the energy of the bound state, we use the fact that the energy difference between two states determines how fast their relative phase grows with time. Therefore, we prepare the bound state in a superposition with the state that has no photons and measure their phase difference as a function of time and space. So, to convert the result of this measure into a dispersion relation, we use a Fourier transform, which translates position and time into momentum and energy, respectively. We are left with the familiar energy-momentum relationship of excitations in a network.
 |
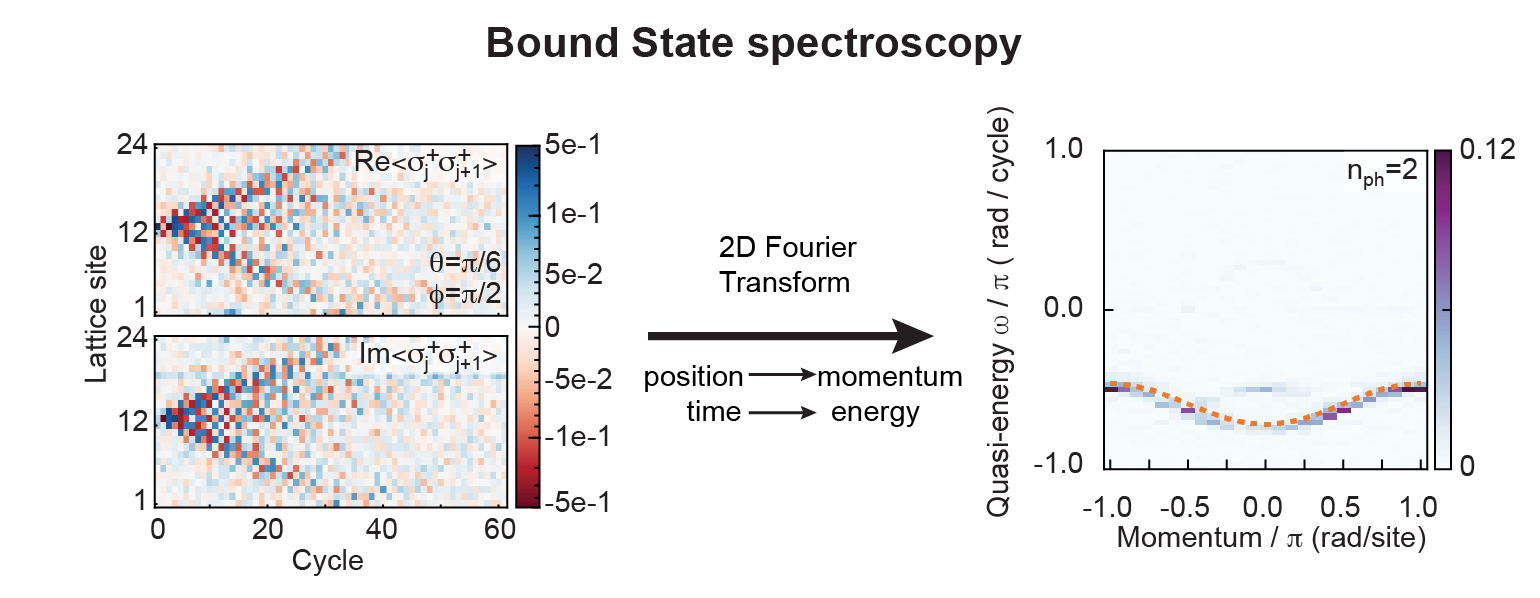| Spectroscopy of bound states. We compare the phase accumulation of a north-United state of photons with that of vacuum (without photons) depending on the site and time of the network. a 2d Fourier transform yields the dispersion relation of the quasiparticle in the bound state. |
break integrability
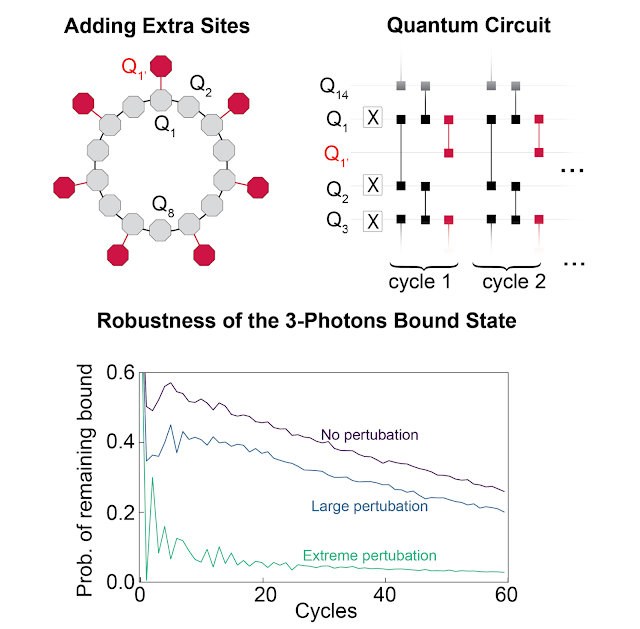
The above system is “integrable”, which means that it has a sufficient number of conserved quantities that its dynamics is restricted to a small part of the available computational space. In such integrable regimes, the appearance of bound states is not so surprising. In fact, bound states in similar systems were foretold in 2012, then observed in 2013. However, these linked states are fragile and their existence is generally thought to stem from integrability. For more complex systems, there is less symmetry and integrability is quickly lost. Our initial idea was to investigate how these bound states disappear as we break the integrability to better understand their rigidity.
To break integrability, we modify which qubits are connected with fSim gates. We add qubits so that at alternate sites, in addition to jumping to each of its two nearest neighbor sites, a photon can also jump to a third site oriented radially outward from the ring.
Although a bound state is restricted to a very small part of the phase space, we expected that the chaotic behavior associated with integrability breaking would allow the system to explore the phase space more freely. This would cause bound states to break. We find that this is not the case. Even when the integrability break is so strong that photons have the same probability of jumping to the third site as to either of the two adjacent sites in the ring, the bound state remains intact, until the decoherence effect causes them to slowly decay. (see document for more details).
 |
| Top: New geometry to break the integrability. The alternate sites are connected to a third site facing radially outward. This increases the complexity of the system and allows for potentially chaotic behavior. Bottom: Despite this added complexity that takes the system beyond integrability, we find that the 3-photon bound state remains stable even for a relatively large perturbation. The probability of being tied down slowly decreases due to decoherence (see article). |
Conclution
We do not yet have a satisfactory explanation for this unexpected resistance. We speculate that it may be related to a phenomenon called prethermalization, where disproportionate energy scales in the system can prevent a system from reaching thermal equilibrium as quickly as it would otherwise. We believe that future research will lead to new insights into many-body quantum physics, including the interaction of prethermalization and integrability.
Thanks
We would like to thank our quantum science communicator Katherine McCormick for her help in writing this blog post.
