Input space modal connectivity in deep neural networks is based on research on excessive input invariance, blind spots, and connectivity between inputs that produce similar outputs. The phenomenon exists in general, even in untrained networks, as demonstrated by empirical and theoretical findings. This research extends the scope of input space modal connectivity beyond out-of-distribution samples, considering all possible inputs. The study adapts methods from parameter space modal connectivity to explore the input space, providing insights into the behavior of neural networks.
The research builds on previous work identifying low-loss high-dimensional convex hulls between multiple loss minimizers, which is crucial for analyzing training dynamics and mode connectivity. Feature visualization techniques, which optimize inputs for adversarial attacks, further contribute to understanding input space manipulation. By synthesizing these diverse areas of study, the research presents a comprehensive view of input space mode connectivity, emphasizing its implications for adversarial detection and model interpretability, while highlighting the intrinsic properties of high-dimensional geometry in neural networks.
The concept of modal connectivity in neural networks extends from parameter space to input space, revealing low-loss paths between inputs that yield similar predictions. This phenomenon, observed in both trained and untrained models, suggests a geometric effect explainable through percolation theory. The study employs real, interpolated, and synthetic inputs to explore input space connectivity, demonstrating its prevalence and simplicity in trained models. This research advances the understanding of neural network behavior, particularly with regard to adversarial examples, and offers potential applications in adversarial detection and model interpretability. The findings provide new insights into the high-dimensional geometry of neural networks and their generalization capabilities.
The methodology employs various input generation techniques, including real, interpolated, and synthetic images, to comprehensively analyze input space connectivity in deep neural networks. The loss landscape analysis investigates the barriers between different modes, with a particular focus on natural inputs and adversarial examples. The theoretical framework uses percolation theory to explain input space mode connectivity as a geometric phenomenon in high-dimensional spaces. This approach provides a foundation for understanding connectivity properties in both trained and untrained networks.
Empirical validation on pre-trained vision models demonstrates the existence of low-loss paths between different modes, supporting theoretical claims. An adversarial detection algorithm developed from these findings highlights practical applications. The methodology is extended to untrained networks, emphasizing that input-space mode connectivity is a fundamental feature of neural architectures. Consistent use of cross-entropy loss as an evaluation metric ensures comparability across experiments. This comprehensive approach combines theoretical insights with empirical evidence to explore input-space mode connectivity in deep neural networks.
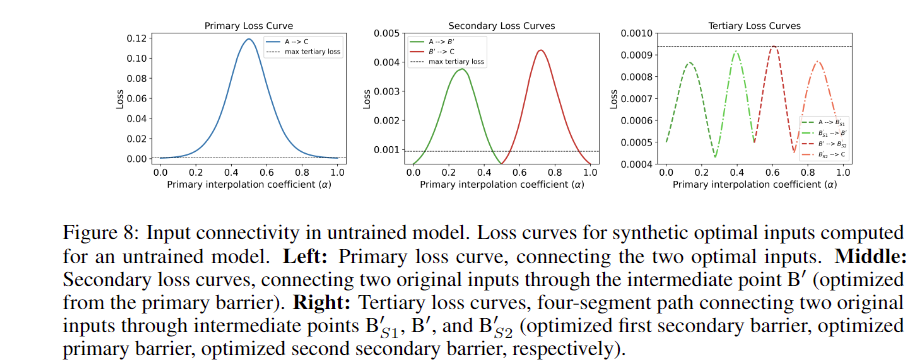
The results extend mode connectivity to the input space of deep neural networks, revealing low-loss paths between inputs, yielding similar predictions. Trained models exhibit simple, nearly linear paths between connected inputs. The research distinguishes natural inputs from adversarial examples based on loss barrier heights, with real-real pairs exhibiting low barriers and real-adversarial pairs exhibiting high, complex barriers. This geometric phenomenon, explained through percolation theory, persists in untrained models. The findings enhance understanding of model behavior, improve adversarial detection methods, and contribute to the interpretability of deep neural networks.
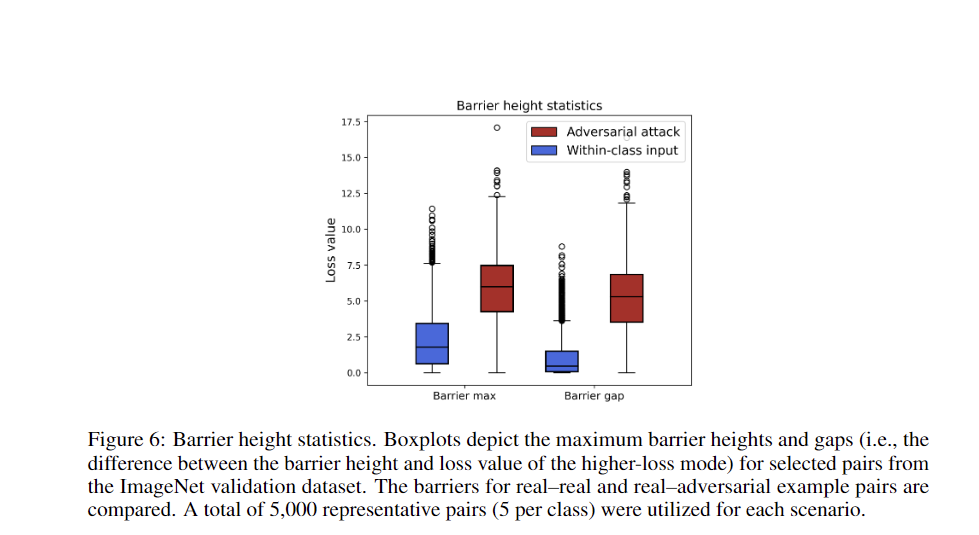
In conclusion, the research demonstrates the existence of modal connectivity in the input space of deep networks trained for image classification. Low-loss paths consistently connect different modes, revealing a robust structure in the input space. The study differentiates natural inputs from adversarial attacks based on the heights of loss barriers along linear interpolation paths. This knowledge advances adversarial detection mechanisms and improves the interpretability of deep neural networks. The findings support the hypothesis that modal connectivity is an intrinsic property of high-dimensional geometry, explainable through percolation theory.
Take a look at the PaperAll credit for this research goes to the researchers of this project. Also, don't forget to follow us on twitter.com/Marktechpost”>twitter and join our Telegram Channel and LinkedIn GrAbove!. If you like our work, you will love our fact sheet..
Don't forget to join our SubReddit of over 50,000 ml
FREE ai WEBINAR: 'SAM 2 for Video: How to Optimize Your Data' (Wednesday, September 25, 4:00 am – 4:45 am EST)

Shoaib Nazir is a Consulting Intern at MarktechPost and has completed his dual M.tech degree from Indian Institute of technology (IIT) Kharagpur. Being passionate about data science, he is particularly interested in the various applications of artificial intelligence in various domains. Shoaib is driven by the desire to explore the latest technological advancements and their practical implications in everyday life. His enthusiasm for innovation and solving real-world problems fuels his continuous learning and contribution to the field of ai.
<script async src="//platform.twitter.com/widgets.js” charset=”utf-8″>






