Introducción
¿Alguna vez has reflexionado sobre la mecánica detrás del reconocimiento de voz de tu teléfono inteligente o las complejidades del pronóstico del tiempo? En ese caso, es posible que le intrigue descubrir el papel fundamental que desempeñan los modelos ocultos de Markov (HMM). Estas construcciones matemáticas han provocado profundas transformaciones en ámbitos como el reconocimiento de voz, el procesamiento del lenguaje natural y la bioinformática, permitiendo a los sistemas desentrañar las complejidades de los datos secuenciales. Este artículo analizará brevemente los modelos ocultos de Markov, sus aplicaciones, componentes, metodologías de decodificación y más.
Objetivos de aprendizaje
- Comprender los componentes fundamentales de los modelos ocultos de Markov (HMM), incluidos estados, observaciones, probabilidades de transición, probabilidades de emisión y probabilidades de estado inicial.
- Explore los principales algoritmos de decodificación para HMM: el algoritmo directo, el algoritmo de Viterbi y el algoritmo de Baum-Welch, y sus aplicaciones en reconocimiento de voz, bioinformática y más.
- Reconozca las limitaciones y desafíos de los HMM y aprenda cómo mitigarlos, como la sensibilidad a la inicialización, los supuestos de independencia y los requisitos de cantidad de datos.
Modelos ocultos de Markov
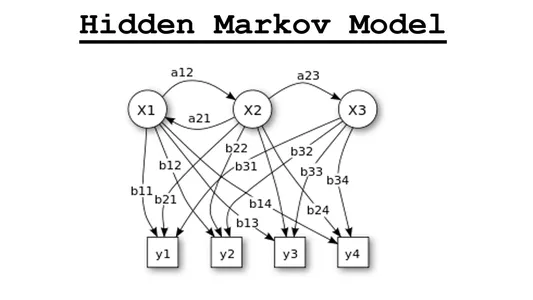
Los modelos ocultos de Markov (HMM), introducidos por Baum LE en 1966, son modelos estadísticos potentes. Revelan estados ocultos dentro de un proceso de Markov utilizando datos observados. Los HMM son fundamentales en el reconocimiento de voz, reconocimiento de caracteres, comunicación móvil, bioinformática y diagnóstico de fallas. Cubren la brecha entre eventos atendidos y estados a través de distribuciones de probabilidad. Los HMM son doblemente estocásticos y combinan una cadena de Markov primaria con procesos que conectan estados y observaciones. Se destacan en decodificar tendencias en datos de vigilancia, adaptarse a patrones cambiantes e incorporar elementos como la estacionalidad. En la vigilancia de series temporales, los HMM son invaluables e incluso se extienden a aplicaciones de información espacial.
Aplicaciones de los HMM
Los modelos ocultos de Markov (HMM) encuentran diversas aplicaciones en varios dominios debido a su capacidad para modelar datos secuenciales y estados ocultos. Exploremos cómo se aplican los HMM en diferentes campos:
- Identificación humana mediante la marcha: Los HMM son fundamentales para identificar individuos en función de sus patrones de marcha únicos. Al modelar los estilos distintivos de caminar de las personas, los HMM ayudan a diferenciar a una persona de otra. Esta aplicación es crucial en sistemas de seguridad y control de acceso, mejorando los métodos de identificación biométrica al incorporar el análisis de la marcha humana.
- Reconocimiento de acciones humanas a partir de imágenes secuenciales en el tiempo: Los HMM son cruciales para reconocer y categorizar acciones humanas a partir de imágenes secuenciales o cuadros de video. Al capturar las dependencias temporales y las transiciones entre diferentes poses y acciones, los HMM permiten una identificación precisa de las diversas actividades que realizan los individuos. Esta aplicación se utiliza en vigilancia, análisis de vídeo y evaluación del rendimiento deportivo, entre otros ámbitos.
- Identificación de expresiones faciales a partir de vídeos: En la informática afectiva y la interacción persona-computadora, los HMM se utilizan para analizar expresiones faciales en videos. Ayudan a reconocer e interpretar emociones y cambios de humor al capturar la dinámica temporal de los movimientos y expresiones de los músculos faciales. Esta aplicación es fundamental para comprender las experiencias de los usuarios, las respuestas emocionales y las señales de comunicación no verbal en varios sistemas interactivos.
Componentes básicos de los HMM
Los modelos ocultos de Markov (HMM) tienen varios componentes fundamentales que definen su estructura y funcionalidad. Comprender estos componentes es crucial para trabajar con HMM de manera efectiva. Estos son los componentes esenciales de los HMM:
- Estados (S)
- Observaciones (O)
- Probabilidades de transición (A)
- Probabilidades de emisión (B)
- Probabilidades del estado inicial (π)
- Espacio de estados (S)
- Espacio de observación (O)
Algoritmos de decodificación
En la siguiente tabla, describimos los tres algoritmos de decodificación principales, junto con sus descripciones, aplicaciones y ventajas:
| Algoritmo | Descripción | Solicitud |
| Algoritmo directo | Calcula la probabilidad de datos observados dado un HMM, utilizado en reconocimiento de voz y procesamiento del lenguaje natural. | – Reconocimiento de voz – Procesamiento del lenguaje natural – Etiquetado de partes del discurso – Reconocimiento de entidades nombradas – Traducción automática |
| Algoritmo de Viterbi | Identifica la secuencia más probable de estados ocultos que generaron datos observados, aplicados en reconocimiento de voz y bioinformática. | – Reconocimiento de voz – Bioinformática – Alineación de secuencias – Predicción genética |
| Algoritmo de Baum-Welch | Estima los parámetros del modelo HMM basándose en datos observados, comúnmente utilizados en bioinformática y reconocimiento de voz. | – Bioinformática – Predicción genética – Reconocimiento de voz – Adaptación de modelos |
Ejemplos de uso de HMM
A continuación se muestran algunos ejemplos de cómo se utilizan los HMM en diferentes dominios:
- Reconocimiento de voz: Los HMM son la base de muchos sistemas automáticos de reconocimiento de voz. Modelan fonemas y sus transiciones, permitiendo la conversión precisa del lenguaje hablado en texto. Los asistentes virtuales como Siri y Alexa utilizan HMM para comprender y responder a comandos de voz.
- Procesamiento del lenguaje natural (PNL): Los HMM se aplican a tareas como el etiquetado de partes del discurso, el reconocimiento de entidades nombradas y la traducción automática. Ayudan a comprender la estructura y el significado del lenguaje humano, mejorando la precisión de las aplicaciones de PNL.
- Bioinformática: Los HMM se utilizan ampliamente para la predicción de genes, la predicción de estructuras de proteínas y la alineación de secuencias. Ayudan a decodificar la gran cantidad de datos biológicos disponibles y ayudan en el análisis y la anotación del genoma.
- Finanzas: Los HMM encuentran aplicaciones en modelos y pronósticos financieros. Se utilizan para análisis de tendencias de mercado, fijación de precios de activos y evaluación de riesgos, lo que ayuda a tomar decisiones de inversión informadas y gestión de riesgos.
- Predicción del tiempo: Los meteorólogos utilizan HMM para modelar la evolución de los patrones climáticos. Pueden predecir condiciones climáticas futuras y eventos climáticos severos mediante el análisis de datos meteorológicos históricos y parámetros observables.
Decodificación de HMM: paso a paso
Aquí hay una guía paso a paso para decodificar HMM:
1. Inicialización del modelo: Comience con un modelo HMM inicial, que abarque parámetros como probabilidades de transición y emisión, generalmente inicializados con conjeturas fundamentadas o aleatoriedad.
2. Algoritmo directo: Calcule la probabilidad de observar la secuencia de datos calculando las probabilidades directas para cada estado en cada paso de tiempo.
3. Algoritmo de Viterbi: Encuentre la secuencia de estados ocultos más probable considerando las probabilidades de transición y emisión.
4. Algoritmo de Baum-Welch: Aplicar esta técnica de maximización de expectativas para refinar los parámetros del HMM mediante la estimación de probabilidades mejoradas de transición y emisión.
5. Iteración: Itera continuamente entre los pasos 2 y 4 hasta que los parámetros del modelo convergen a sus valores óptimos, mejorando la alineación del modelo con los datos observados para una mayor precisión.
Limitaciones y desafíos
| Limitaciones y desafíos | Descripción | Mitigación o consideraciones |
| Sensibilidad a la inicialización | El rendimiento de los HMM depende de los parámetros iniciales, lo que corre el riesgo de obtener soluciones subóptimas. | Utilice análisis de sensibilidad como bootstrapping o búsqueda de cuadrícula para una selección sólida de modelos. |
| Asunción de la Independencia | Los HMM asumen una independencia condicional de los datos observados, lo que no se cumple en sistemas complejos. | Considere modelos complejos como los modelos ocultos de Semi-Markov (HSMM) para capturar dependencias de mayor alcance. |
| Memoria limitada | Los HMM tienen memoria finita. Limitar el modelado de dependencia a largo plazo. | Elija HMM de orden superior o modelos alternativos con memoria extendida, como redes neuronales recurrentes (RNN) o redes de memoria larga a corto plazo (LSTM). |
| Cantidad de datos | Los HMM requieren datos sustanciales, lo que plantea desafíos en dominios con escasez de datos. | Aplique el aumento de datos, la recopilación de datos de dominios específicos o transfiera el aprendizaje para abordar las limitaciones de los datos. |
| Estructura del modelo complejo | La creciente complejidad del modelo puede dificultar el ajuste de los datos. | Emplear técnicas de selección de modelos, como validación cruzada y criterios de información, para equilibrar la complejidad del modelo y evitar el sobreajuste. |
Mejores prácticas y consejos
A continuación se ofrecen algunos consejos para utilizar los HMM de forma eficaz:
- Preprocesamiento exhaustivo de datos: Antes de entrenar un HMM, asegúrese de realizar un preprocesamiento exhaustivo de los datos, incluida la limpieza, normalización y extracción de características de los datos. Este paso ayuda a eliminar el ruido y la información irrelevante, mejorando la calidad de los datos de entrada y mejorando el rendimiento del modelo.
- Selección cuidadosa del modelo: Elija la variante HMM adecuada según los requisitos específicos de la aplicación. Considere factores como la complejidad de los datos, la presencia de dependencias y la necesidad de memoria. Opte por modelos más avanzados como los modelos ocultos Semi-Markov (HSMM) o HMM de orden superior cuando sea necesario.
- Entrenamiento de modelo robusto: Implemente potentes técnicas de entrenamiento de modelos, como el algoritmo de Baum-Welch o la estimación de máxima verosimilitud, para garantizar que el modelo aprenda de los datos de forma eficaz. Emplee técnicas como la validación cruzada para evaluar el rendimiento del modelo y evitar el sobreajuste.
- Evaluación y actualización periódica del modelo: Evalúe continuamente el rendimiento del modelo con nuevos datos y actualice los parámetros del modelo en consecuencia. Vuelva a entrenar periódicamente el modelo con nuevos datos para garantizar que siga siendo relevante y preciso a lo largo del tiempo, especialmente en entornos dinámicos.
- Documentación e interpretabilidad: Mantenga una documentación completa del proceso de desarrollo del modelo, incluido el razonamiento detrás de la elección de parámetros y cualquier suposición hecha durante el modelado. Asegúrese de que los resultados del modelo sean interpretables y proporcionen información sobre los estados ocultos y sus implicaciones para los datos observados.
Conclusión
Los modelos ocultos de Markov son una herramienta extraordinaria para modelar y decodificar datos secuenciales y ofrecen aplicaciones en diversos campos, como el reconocimiento de voz, la bioinformática, las finanzas y más. Al comprender sus componentes esenciales, algoritmos de decodificación y aplicaciones del mundo real, puede abordar problemas complejos y hacer predicciones en escenarios donde las secuencias son críticas.
Conclusiones clave
- Los modelos ocultos de Markov (HMM) son modelos estadísticos versátiles que revelan estados ocultos dentro de datos secuenciales y son cruciales en campos como el reconocimiento de voz, la bioinformática y las finanzas.
- Los tres algoritmos de decodificación principales para HMM (algoritmo directo, algoritmo de Viterbi y algoritmo de Baum-Welch) permiten tareas como el reconocimiento de voz, la predicción de genes y la estimación de parámetros del modelo, mejorando nuestra comprensión de los datos secuenciales.
- Al trabajar con HMM, es esencial ser consciente de sus limitaciones y desafíos, como la sensibilidad a los requisitos de inicialización y cantidad de datos, y emplear las mejores prácticas como el preprocesamiento exhaustivo de datos y la capacitación sólida de modelos para superar estos desafíos y lograr resultados precisos.
Preguntas frecuentes
R. Un modelo oculto de Markov (HMM) es un modelo matemático utilizado para representar sistemas con estados ocultos que generan datos observables a través de procesos probabilísticos, lo que permite el análisis y predicción de secuencias de datos. Consta de estados ocultos, datos observados, transición, emisión y probabilidades de estado inicial.
R. La formulación del Modelo Oculto de Markov (HMM) implica una secuencia de estados ocultos y una secuencia correspondiente de datos observables. Incorpora probabilidades de transición, emisión y estado inicial para describir cómo los estados ocultos generan datos observados a lo largo del tiempo.
Los modelos ocultos de Markov (HMM) se utilizan principalmente para dos tareas: 1. Estimación: determinar la probabilidad de los datos observados dado el modelo, y 2. Decodificación: encontrar la secuencia más probable de estados ocultos dados los datos observados.
 NEWSLETTER
NEWSLETTER





