Beyond Guesswork: Leveraging Bayesian Statistics for Effective Article Title Selection

Having a good title is crucial to the success of an article. People spend just a second (if we believe Ryan Holiday's book) “Believe me, I'm lying” Decide whether to click on the title to open the full article. The media is obsessed with optimizing click-through rate (CTR), the number of clicks a title receives divided by the number of times the title is displayed. Having a clickbait title increases CTR. Media outlets are likely to choose a title with a higher CTR between the two because this will generate more revenue.

I'm not really interested in squeezing out ad revenue. It's more about spreading my knowledge and experience. And yet, viewers have limited time and attention, while content on the Internet is virtually unlimited. Therefore, I have to compete with other content creators to capture the attention of viewers.

How do I choose a suitable title for my next article? Of course, I need a set of options to choose from. Hopefully I can generate them myself or ask ChatGPT. But what do I do next? As a data scientist, I suggest conducting an A/B/N test to understand which option is the best based on data. But there is a problem. First, I need to decide quickly because content expires quickly. Second, there may not be enough observations to detect a statistically significant difference in CTRs, since these values ​​are relatively low. So there are other options besides waiting a couple of weeks to decide.

I hope there is a solution! I use a “many-armed bandit” machine learning algorithm that adapts to the data we observe about viewer behavior. The more people click on a particular option in the set, the more traffic we can allocate to that option. In this article, I will briefly explain what a “Bayesian multi-armed bandit” is and show how it works in practice using Python.

Multi-armed bandits They are machine learning algorithms. The Bayesian type uses Thompson sampling choose an option based on our prior beliefs about the probability distributions of CTRs that are subsequently updated based on new data. All this talk of probability theory and mathematical statistics can seem complex and daunting. Let me explain the entire concept using as few formulas as possible.

Suppose there are only two titles to choose from. We have no idea about their CTRs. But we want to have the highest performance title. We have multiple options. The first is to choose the title in which we believe the most. This is how it worked for years in the industry. The second allocates 50% of the incoming traffic to the first title and 50% to the second. This became possible with the rise of digital media, where you can decide precisely what text to display when a viewer requests a list of articles to read. With this approach, you can be sure that 50% of the traffic was assigned to the best performing option. Is this a limit? Of course not!

Some people would read the article a couple of minutes after it was published. Some people would do it in a couple of hours or days. This means we can look at how “early” readers responded to different titles and change the traffic allocation from 50/50 and allocate a little more to the better performing option. After a while, we can recalculate the CTRs and adjust the split. As a limit, we want to adjust the traffic allocation after each new viewer clicks or skips the title. We need a framework to adapt traffic allocation in a scientific and automated way.

Here comes Bayes' theorem, Beta distribution and Thompson sampling.

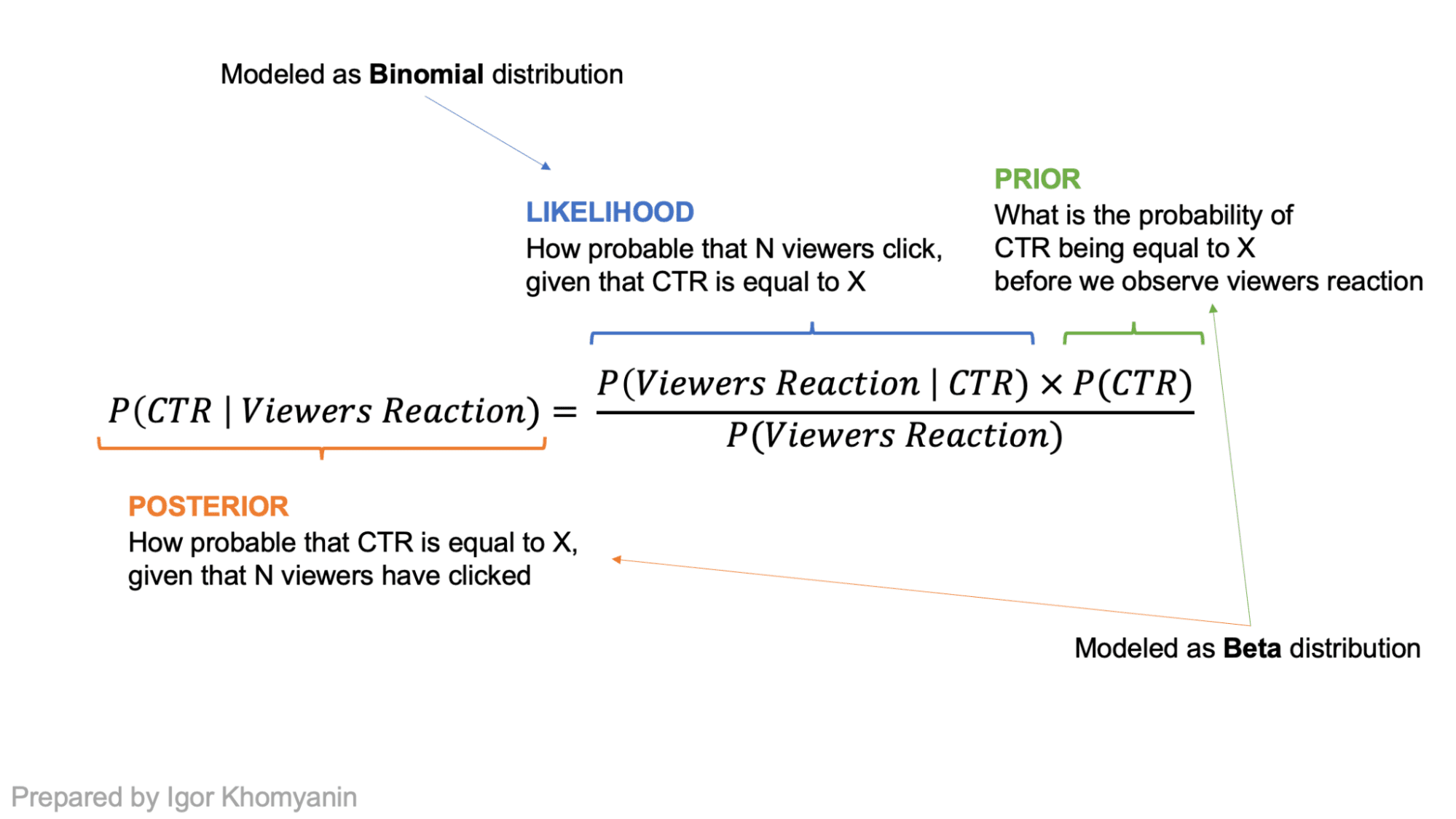
Suppose the CTR of an article is a “theta” random variable. By design, it lies between 0 and 1. If we have no prior beliefs, it can be any number between 0 and 1 with equal probability. After observing some data “x”, we can adjust our beliefs and have a new distribution for “theta” that will be closer to 0 or 1 using Bayes' theorem.

The number of people who click on the title can be modeled as a Binomial distribution where “n” is the number of visitors who view the title and “p” is the CTR of the title. This is our probability! If we model the above (our belief about the CTR distribution) as a Beta distribution and taking binomial probability, the posterior would also be a Beta distribution with different parameters! In such cases, the Beta distribution is called previous conjugate to probability.

Proving this fact is not that difficult, but it requires some mathematical exercise that is not relevant in the context of this article. Check out the beautiful proof. here:

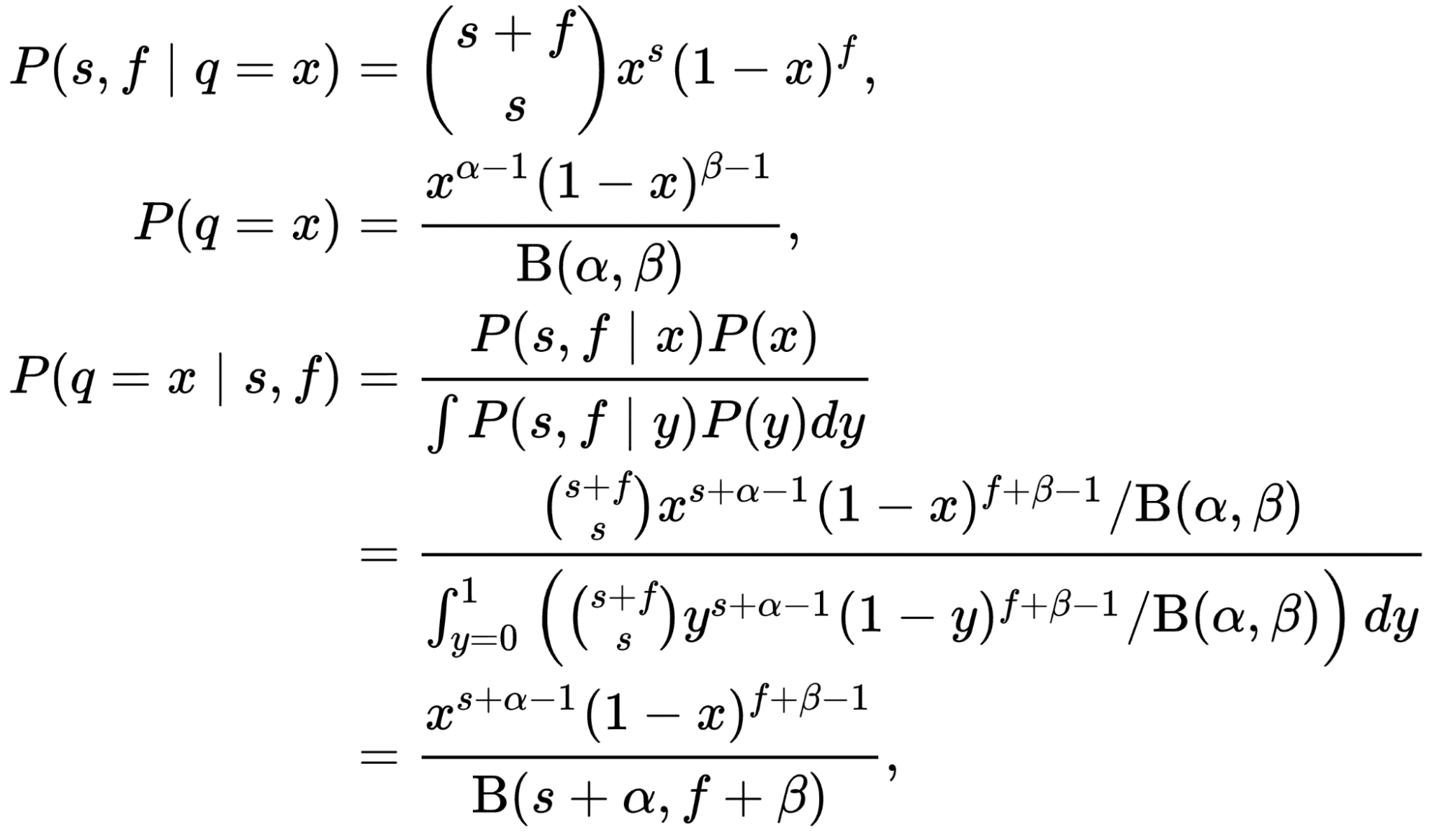
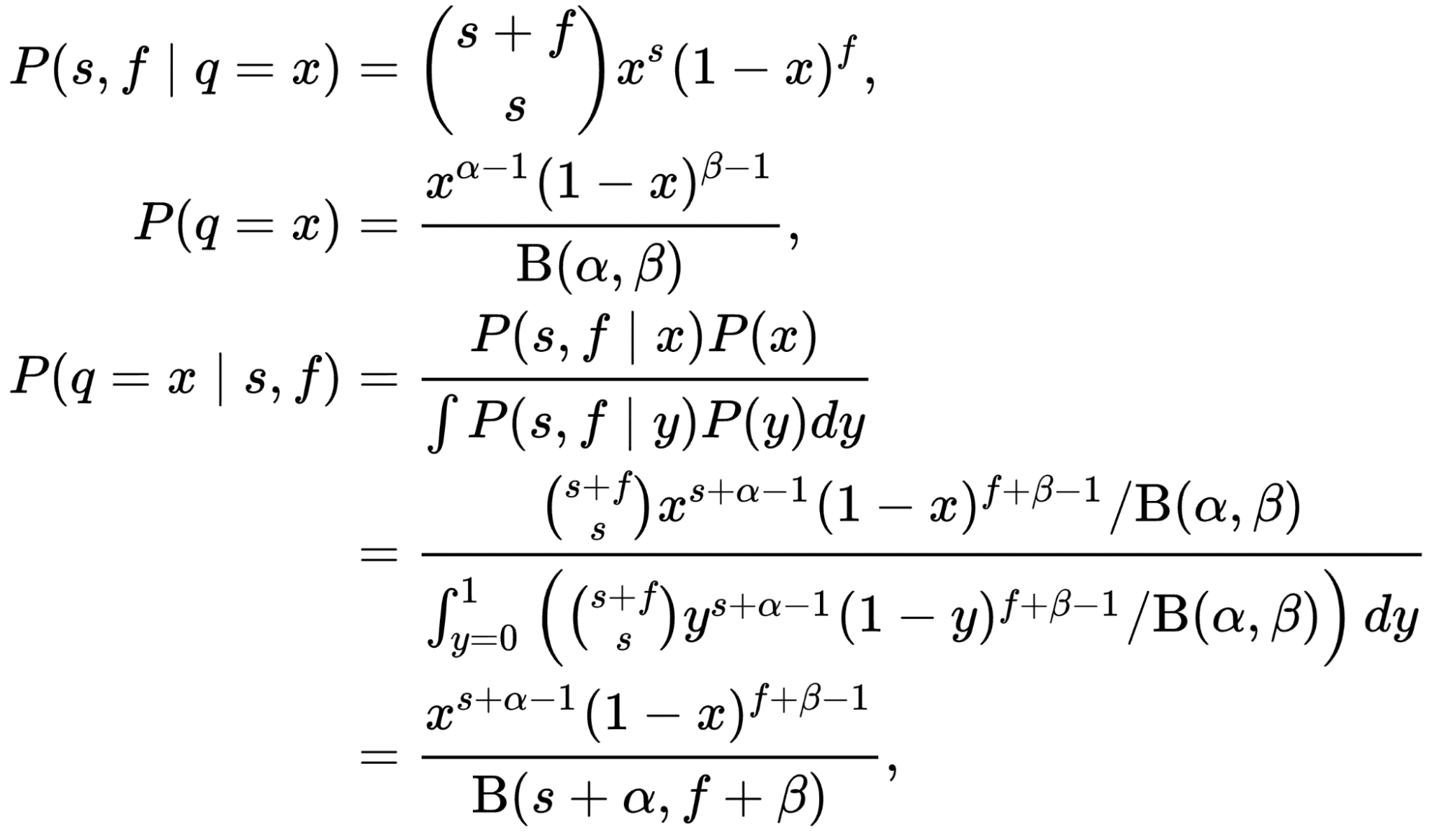
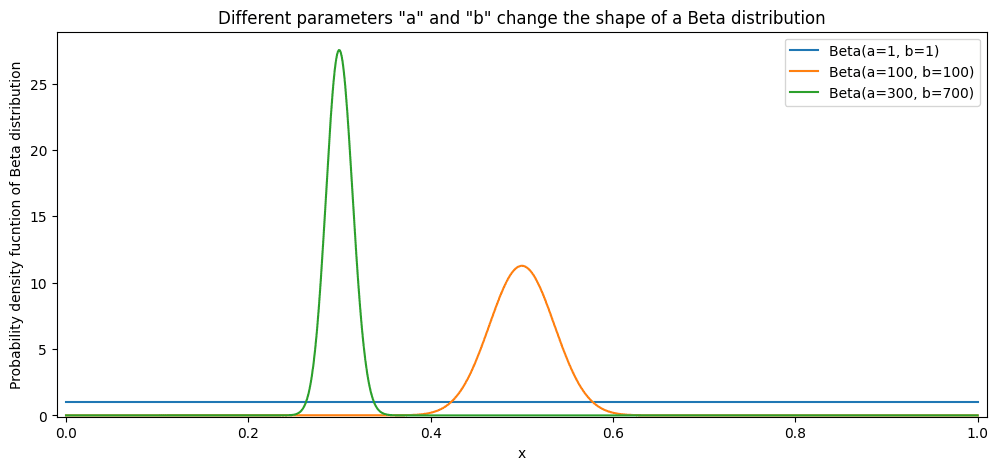
The beta distribution is bounded by 0 and 1, making it a perfect candidate for modeling a CTR distribution. We can start from “a = 1” and “b = 1” as Beta distribution parameters that model the CTR. In this case, we would have no beliefs about the distribution, which would make any CTR equally probable. Then we can start adding observed data. As you can see, each “success” or “click” increases “a” by 1. Each “failure” or “jump” increases “b” by 1. This distorts the CTR distribution but does not change the distribution family. It's still a beta distribution!

We assume that CTR can be modeled as a Beta distribution. Then, there are two title options and two layouts. How do we choose what to show the viewer? Therefore, the algorithm is called “multi-armed bandit”. The moment a viewer requests a title, you “pull both arms” and display CTRs. After that, it compares the values ​​and displays a title with the highest sample CTR. The viewer then clicks or jumps. Clicking on the title would set this option's Beta distribution parameter to “a”, which represents “hits”. Otherwise, it increases the Beta distribution parameter “b” of this option, which means “failures”. This distorts the distribution and, for the next viewer, there will be a different probability of choosing this option (or “arm”) compared to other options.

After several iterations, the algorithm will have an estimate of the CTR distributions. Sampling this distribution will primarily activate the highest CTR arm, but will still allow new users to explore other options and readjust the allocation.

Well, this all works in theory. Is it really better than the 50/50 split we discussed before?

All the code to create a simulation and build graphs can be found in my GitHub repository.

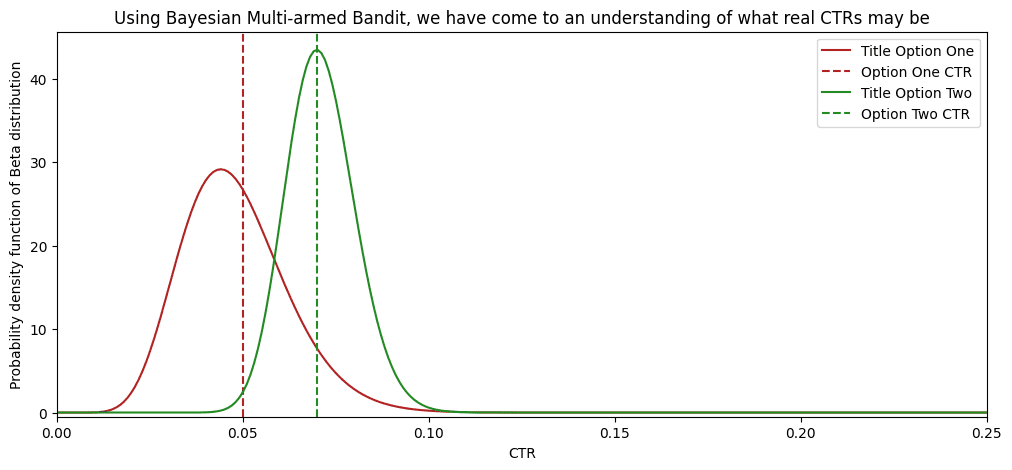
As we mentioned above, we only have two titles to choose from. We have no prior beliefs about the CTRs of this title. So, we start from a=1 and b=1 for both Beta distributions. I will simulate simple incoming traffic assuming a queue of viewers. We know precisely whether the previous viewer “clicked” or “jumped” before showing a title to the new viewer. To simulate “click” and “jump” actions, I need to define some real CTRs. Let them be 5% and 7%. It is essential to mention that the algorithm does not know anything about these values. I need them to simulate a click; you would have real clicks in the real world. I will flip a super biased coin for every title that comes up heads with a probability of 5% or 7%. If heads, you hear a click.

So, the algorithm is simple:

1. Based on the observed data, obtain a Beta distribution for each title.
2. Sample CTR from both distributions
3. Understand which CTR is higher and launch a relevant coin
4. Understand if there was a click or not
5. Increase parameter “a” by 1 if there was a click; increase parameter “b” by 1 if there was a jump
6. Repeat until there are users in the queue.

To understand the quality of the algorithm, we will also save a value that represents a proportion of viewers exposed to the second option, since it has a higher “real” CTR. Let's use a 50/50 split strategy as a counterpart for baseline quality.

Code by author

After 1000 users in the queue, our “multi-armed bandit” already has a good understanding of what the CTRs are.

And here is a graph that shows that such a strategy produces better results. After 100 viewers, the “multi-armed bandit” surpassed 50% of viewers who offered the second option. Because there was more and more evidence supporting the second title, the algorithm assigned more and more traffic to the second title. Almost 80% of all viewers have seen the best performing option! While in the 50/50 split, only 50% of people have seen the best performing option.

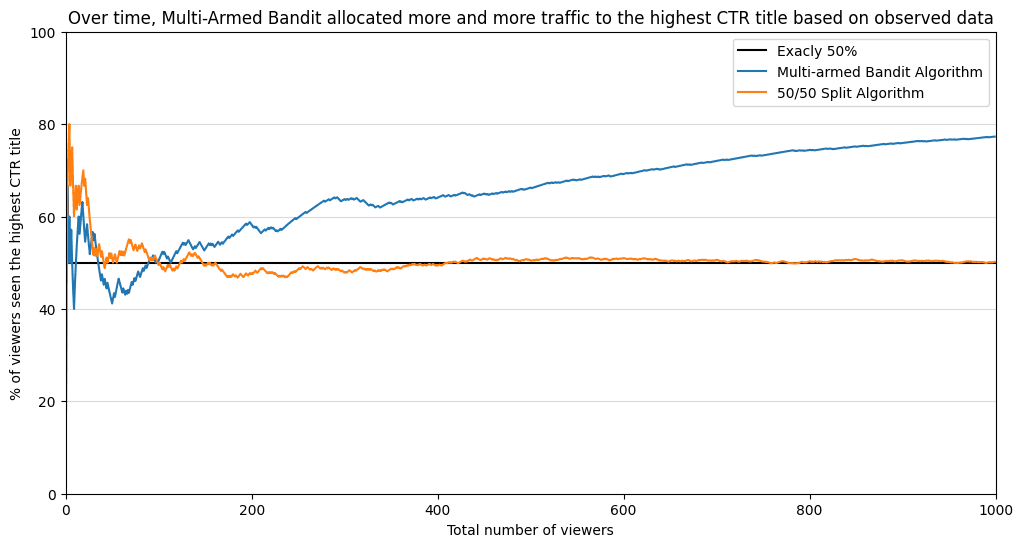
Multi-Armed Bayesian Bandit Exposed an Additional 25% of Viewers to a Better-Performing Option! With more data coming in, the difference will only increase between these two strategies.

Of course, “armed bandits” are not perfect. Sampling and presenting options in real time is expensive. The best thing would be to have a good infrastructure to implement everything with the desired latency. Also, you may not want to scare your viewers by changing the titles. If you have enough traffic to run a quick A/B, do it! Then manually change the title once. However, this algorithm can be used in many other applications beyond media.

I hope you now understand what a “many-armed bandit” is and how it can be used to choose between two options adapted to the new data. I specifically did not focus on mathematics and formulas since textbooks would explain them better. I intend to introduce a new technology and spark interest in it!

If you have any questions, please feel free to contact LinkedIn.

The notebook with all the code can be found in my GitHub repository.

Igor Khomyanin is a data scientist at Salmon, with previous data roles at Yandex and McKinsey. I specialize in extracting value from data through Statistics and Data Visualization.