derivatives they play a central role in optimization and machine learning. Locally approximating a training loss, the derivatives guide an optimizer towards lower values of the loss. Automatic differentiation frameworks like TensorFlow, PyTorchand JAX they are an essential part of modern machine learning, making it feasible to use gradient-based optimizers to train very complex models.
But are derivatives all we need? By themselves, derivatives only tell us how a function behaves in a infinitesimal scale. To use derivatives effectively, we often need to know more than that. For example, to choose a learning rate for gradient descentwe need to know something about how the loss function behaves in a small but finite window. A finite-scale automatic differentiation analogue, if it existed, could help us make those decisions more effectively and thus speed up training.
In our new newspaper “Automatic Taylor Remainder Series Delimitation: Tighter Limits and New Applications“, we present an algorithm called AutoBound that computes the upper and lower bounds of polynomials in a given function, which are valid over a user-specified interval. We then started exploring AutoBound’s applications. In particular, we present a meta-optimizer called SafeRate that uses the upper bounds computed by AutoBound to derive learning rates that guarantee monotonic reduction of a given loss function, without the need for time-consuming hyperparameter tuning. We are also making AutoBound available as open source library.
The AutoBound algorithm
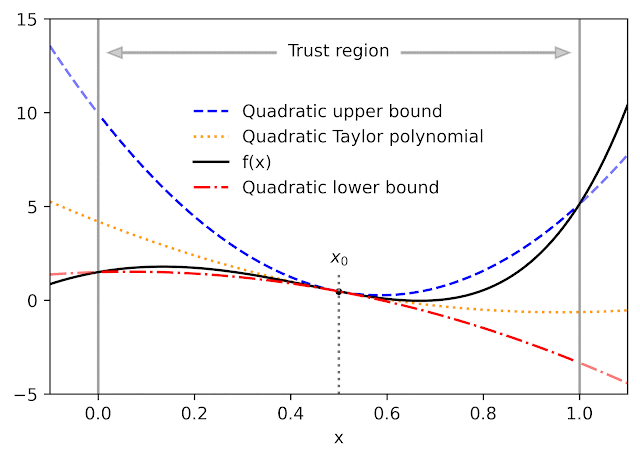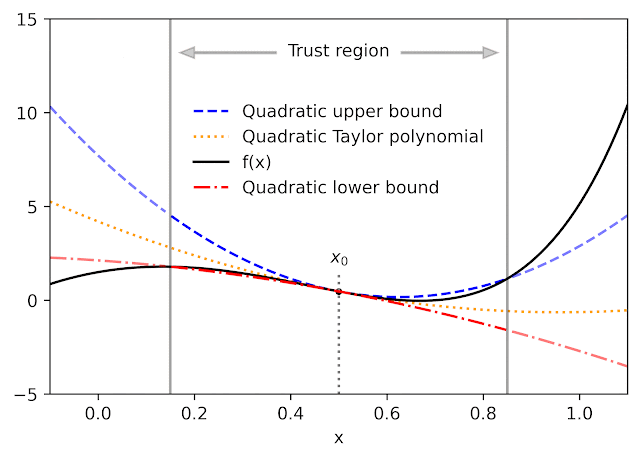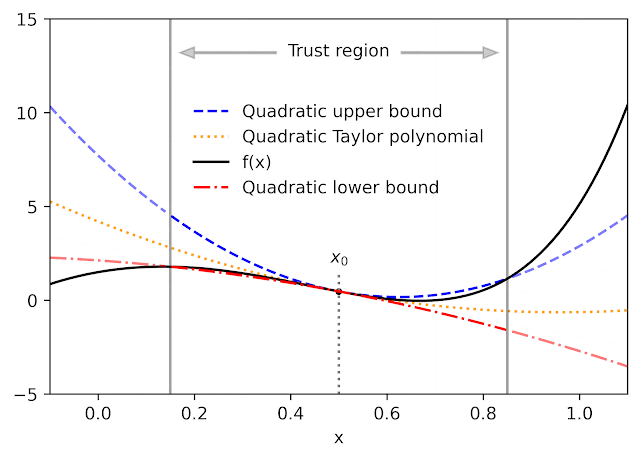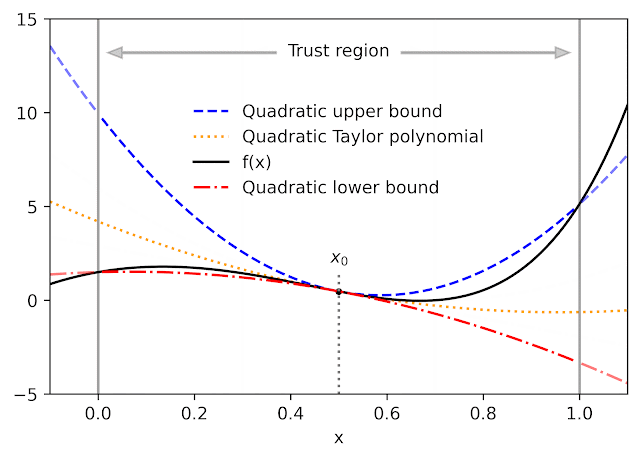
given a function f and a reference point x0AutoBound calculates the upper and lower bounds of the polynomial at f that are held for an interval specified by the called user trusted region. As Taylor polynomialsthe bounding polynomials are equal to f in x0. The bounds become narrower as the trust region narrows and approach the corresponding Taylor polynomial as the width of the trust region approaches zero.
 |
| Quadratic upper and lower bounds automatically derived from a one-dimensional function f, centered at x0=0.5. The upper and lower bounds are valid in a user-specified trust region and become stricter as the trust region shrinks. |
Like automatic differentiation, AutoBound can be applied to any function that can be implemented using standard mathematical operations. In fact, AutoBound is a generalization of Automatic differentiation in Taylor modeand is equivalent to it in the special case where the trusted region has a width of zero.
In order to derive the AutoBound algorithm, there were two main challenges we had to address:
- We had to derive the upper and lower bounds of polynomials for various elementary functions, given an arbitrary reference point and an arbitrary confidence region.
- We had to devise an analogue of the chain of rules to combine these limits.
Limits for elementary functions
For a variety of commonly used functions, we derive optimum upper and lower bounds of the polynomial in closed form. In this context, “optimal” means that the limits are as narrow as possible, among all polynomials where only the maximumdegree coefficient differs from the Taylor series. Our theory applies to elementary functions, such as exp and logand common activation functions of neural networks, such as ReLU and Swish. It builds on and generalizes previous job that applies only to quadratic bounds, and only for an unbounded trust region.
 |
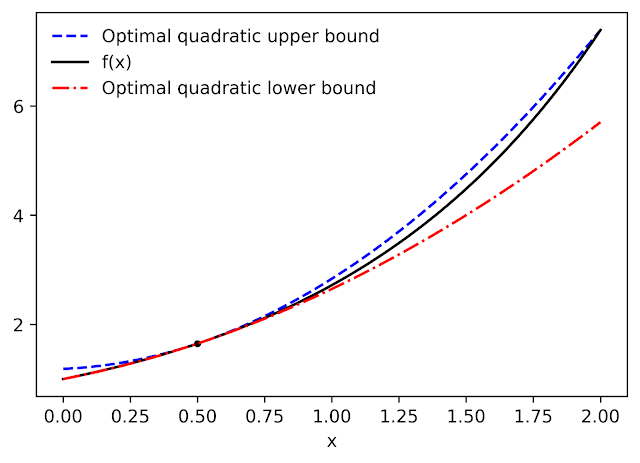| Quadratic optimal upper and lower bounds of the exponential function, centered at x0=0.5 and valid during the interval [0, 2]. |
A new chain rule
To compute the upper and lower limits of arbitrary functions, we derive a generalization of the chain rule that operates on polynomial limits. To illustrate the idea, suppose we have a function that can be written as
and suppose we already have upper and lower polynomial bounds on g and h. How do we calculate the limits of f?
The key turns out to be representing the upper and lower bounds of a given function as single polynomial whose coefficient of highest degree is a interval instead of a scalar. Then we can substitute the limit for h at the limit of gand convert the result back to a polynomial in the same way using interval arithmetic. Under suitable assumptions about the confidence region over which the limit on g holds, it can be shown that this procedure produces the desired limit on f.
 |
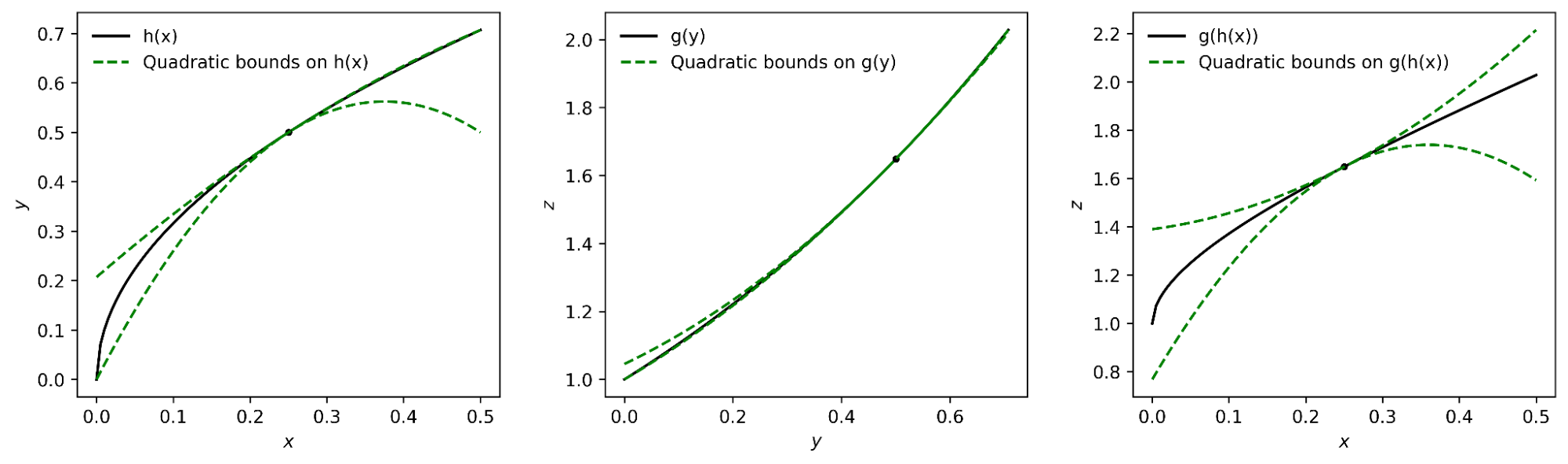| The interval polynomial chain rule applied to the functions h(x) = sqrt(x) and g(y) = exp(y), with x0=0.25 and confidence region [0, 0.5]. |
Our chain rule applies to one-dimensional functions, but also to multivariate functions, such as matrix multiplications and convolutions.
boundary propagation
Using our new chain rule, AutoBound propagates polynomial interval boundaries through a computation graph from inputs to outputs, analogous to automatic differentiation in direct mode.
 |
| Direct propagation of the limits of the interval polynomial for the function f(x) = exp(sqrt(x)). First we compute the (trivial) limits on x, then we use the chain rule to compute the limits on sqrt(x) and exp(sqrt(x)). |
To calculate the limits of a function f(x)AutoBound requires memory proportional to the dimension of x. For this reason, practical applications apply AutoBound to functions with a small number of inputs. However, as we will see, this does not prevent us from using AutoBound for neural network optimization.
Automatically derived optimizers and other applications
What can we do with AutoBound that we can’t do with just AutoBound?
Among other things, AutoBound can be used to automatically derive problem-specific hyperparameter-less optimizers that converge from any starting point. These optimizers iteratively reduce a loss by first using AutoBound to compute an upper bound on the loss that is fitted at the current point, and then minimizing the upper bound to obtain the next point.
 |
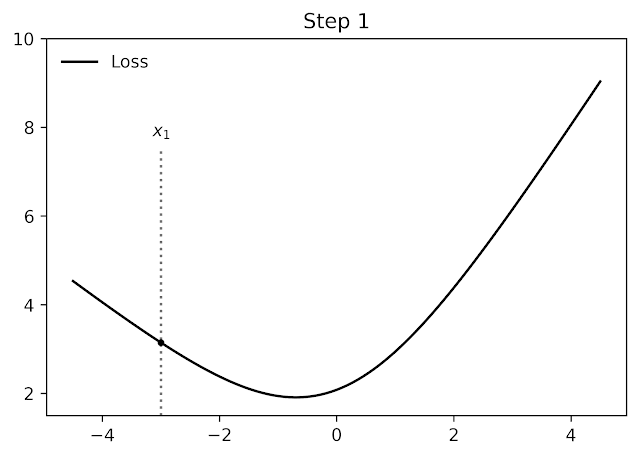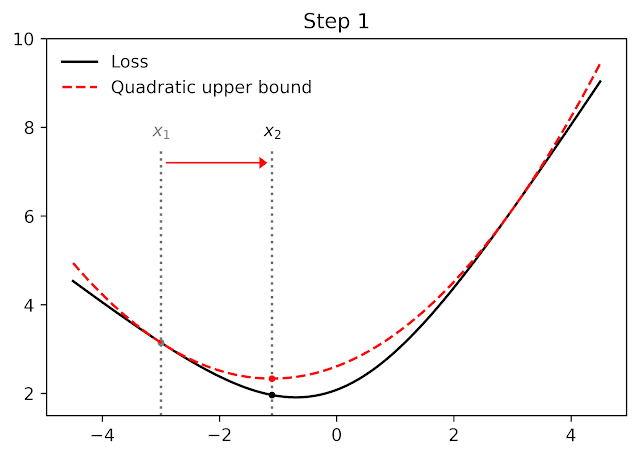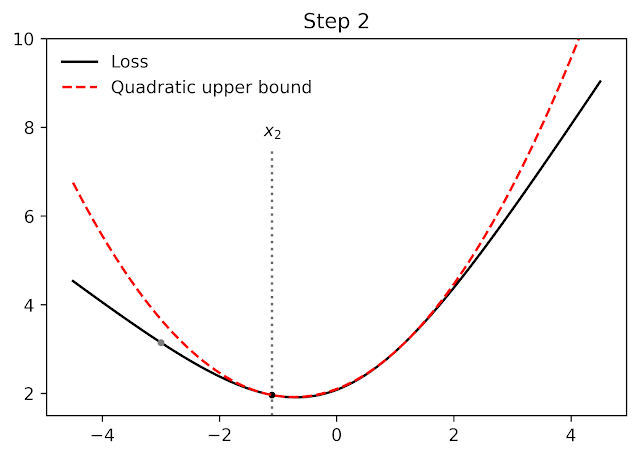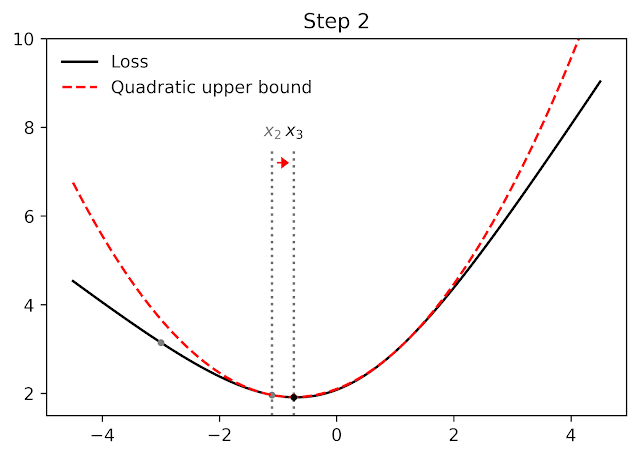| Minimize a one-dimensional logistic regression loss using square upper bounds derived automatically by AutoBound. |
Optimizers that use upper bounds in this way are called majorization-minimization (MM) optimizers. Applied to one-dimensional logistic regression, AutoBound again derives an MM optimizer first published in 2009. Applied to more complex problems, AutoBound derives new MM optimizers that would be difficult to derive by hand.
We can use a similar idea to take an existing optimizer as Adam and make it a non-hyperparameter optimizer that is guaranteed to reduce loss monotonically (in full-batch setup). The resulting optimizer uses the same update direction as the original optimizer, but modifies the learning rate by minimizing a one-dimensional upper bound squared derived from AutoBound. We refer to the resulting meta-optimizer as SafeRate.
 |
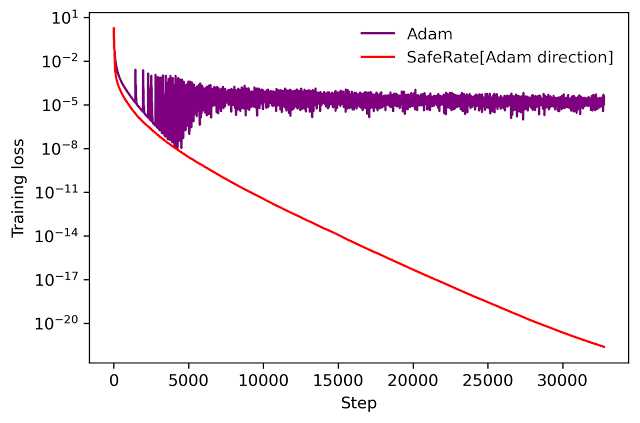| SafeRate performance when used to train a single hidden layer neural network on a subset of the MNIST data set, in full batch configuration. |
Using SafeRate, we can create more robust variants of existing optimizers, at the cost of a single additional step forward that increases the wall time for each step by a small factor (about 2x in the example above).
In addition to the applications just discussed, AutoBound can be used to check numerical integration and automatically test sharper versions of Jensen’s inequalitya fundamental mathematical inequality often used in statistics and other fields.
Improvement over classic limits
limiting the Taylor remainder term automatically not a new idea. A classical technique produces degree k polynomial limits in a function f that are valid in a trusted region [a, b] by first calculating an expression for the kthe derivative of f (using automatic differentiation), then evaluating this expression over [a,b] using interval arithmetic.
While elegant, this approach has some inherent limitations that can lead to very inaccurate limits, as illustrated by the dashed blue lines in the following figure.
 |
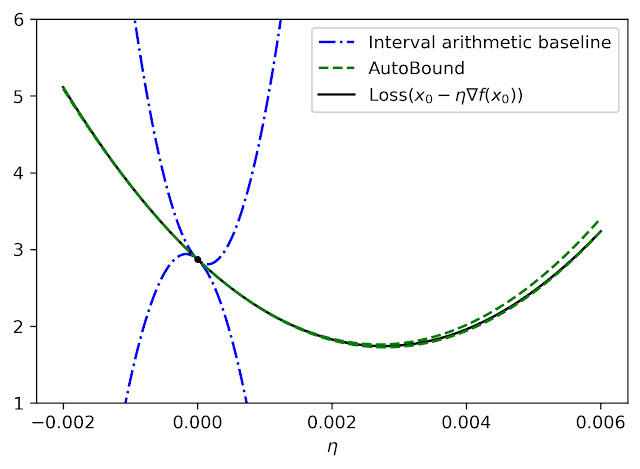| Quadratic upper and lower bounds on the loss of a multiple layer perceptron with two hidden layers, depending on the initial learning rate. The bounds derived from AutoBound are much stricter than those obtained by interval arithmetic evaluation of the second derivative. |
Thinking in the future
Taylor polynomials have been used for over three hundred years and are ubiquitous in numerical optimization and scientific computing. However, Taylor polynomials have significant limitations, which can limit the capabilities of algorithms built on them. Our work is part of a growing literature that recognizes these limitations and seeks to develop a new foundation on which more robust algorithms can be built.
Our experiments so far have only scratched the surface of what’s possible using AutoBound, and we believe it has many applications that we haven’t discovered. To encourage the research community to explore such possibilities, we have made AutoBound available as an open source library built on top of JAX. To get started, visit our github repository.
Thanks
This post is based on joint work with Josh Dillon. We thank Alex Alemi and Sergey Ioffe for valuable comments on an earlier draft of the post.
