
Editor's Image | Midjourney
Bayesian thinking is a way of making decisions using probability. It starts with initial beliefs (priors) and changes them when new evidence comes along (posteriors). This helps make better predictions and better data-driven decisions. It is crucial in fields like artificial intelligence and statistics, where accurate reasoning is important.
Fundamentals of Bayesian Theory
Key Terms
- Prior probability (Prior):Represents the initial belief about the hypothesis.
- Probability:Measures how well the hypothesis explains the evidence.
- Posterior probability (posterior):Combines prior probability and likelihood.
- Evidence:Updates the probability of the hypothesis.
Bayes' Theorem
This theorem describes how to update the probability of a hypothesis based on new information. It is expressed mathematically as:
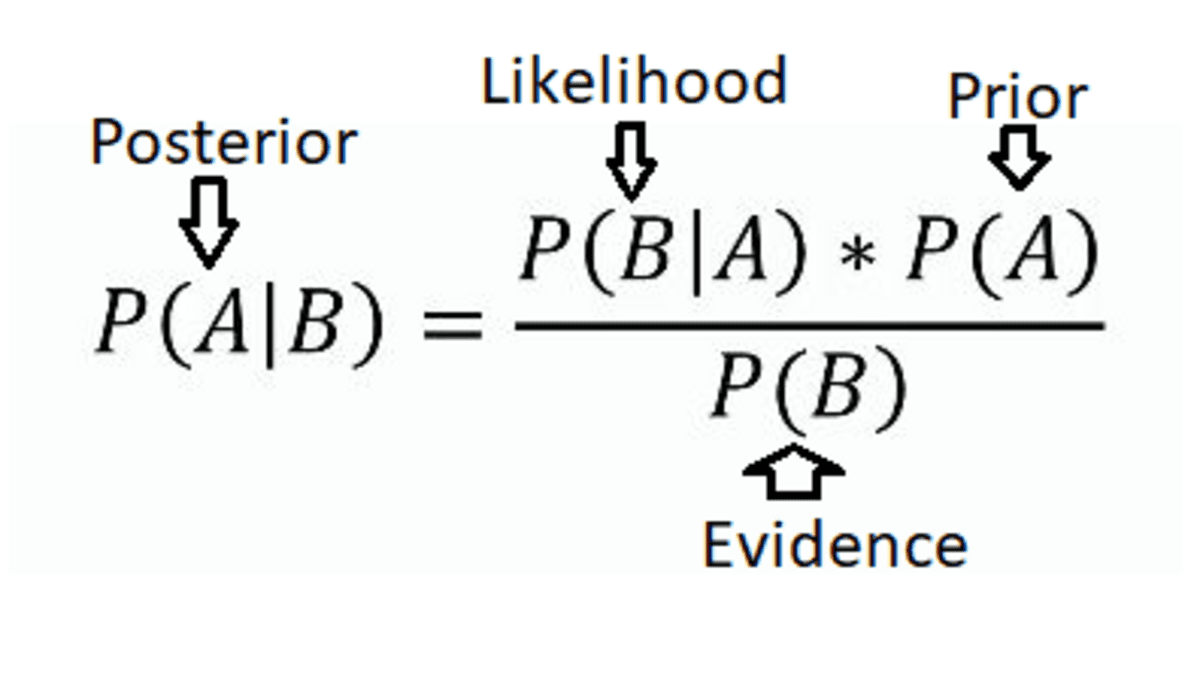
 Bayes' Theorem (Source: Eric Castellanos's Blog)
Bayes' Theorem (Source: Eric Castellanos's Blog)
where:
P(A|B) is the posterior probability of the hypothesis.
P(B|A) Is the probability of the evidence given the hypothesis?
PENNSYLVANIA) is the prior probability of the hypothesis.
P(B) is the overall probability of the evidence.
Applications of Bayesian methods in data science
Bayesian inference
Bayesian inference updates beliefs when things are uncertain. It uses Bayes' theorem to adjust initial beliefs based on new information. This approach combines what is known before with new data in an efficient way. This approach quantifies uncertainty and adjusts probabilities accordingly. In this way, it continuously improves predictions and understanding as more evidence is gathered. It is useful for decision making where uncertainty needs to be managed effectively.
Example: In clinical trials, Bayesian methods estimate the effectiveness of new treatments. They combine prior beliefs from previous studies or with current data. This updates the probability that the treatment will work well. Researchers can then make better decisions using old and new information.
Predictive modeling and uncertainty quantification
Predictive modeling and uncertainty quantification involve making predictions and understanding how confident we are in those predictions. It uses techniques such as Bayesian methods to account for uncertainty and provide probabilistic forecasts. Bayesian modeling is effective for predictions because it manages uncertainty. It not only predicts outcomes, but also indicates our confidence in those predictions. This is achieved through posterior distributions, which quantify uncertainty.
Example: Bayesian regression predicts stock prices by offering a range of possible prices rather than a single prediction. Traders use this range to avoid risk and make investment decisions.
Bayesian neural networks
Bayesian neural networks (BNNs) are neural networks that provide probabilistic results. They provide predictions along with measures of uncertainty. Instead of fixed parameters, BNNs use probability distributions for weights and biases. This allows them to capture and propagate uncertainty through the network. They are useful for tasks that require uncertainty measurement and decision making. They are used in classification and regression.
Example: In fraud detection, Bayesian networks analyze relationships between variables such as transaction history and user behavior to detect unusual patterns linked to fraud. They improve the accuracy of fraud detection systems compared to traditional approaches.
Tools and libraries for Bayesian analysis
There are several tools and libraries available to implement Bayesian methods effectively. Let's take a look at some popular tools.
PyMC4
It is a library for probabilistic programming in Python. It helps with Bayesian modeling and inference. It builds on the strengths of its predecessor, PyMC3. It introduces significant improvements through its integration with JAX. JAX offers automatic differentiation and GPU acceleration. This makes Bayesian models faster and more scalable.
Are
A probabilistic programming language implemented in C++ and available through several interfaces (RStan, PyStan, CmdStan, etc.). Stan excels at performing HMC and NUTS sampling efficiently and is known for its speed and accuracy. It also includes extensive diagnostics and tools for model checking.
TensorFlow Probability
It is a library for probabilistic reasoning and statistical analysis in TensorFlow. TFP provides a variety of distributions, bijectors, and MCMC algorithms. Its integration with TensorFlow ensures efficient execution on various types of hardware. It allows users to seamlessly combine probabilistic models with deep learning architectures. This article helps in making robust, data-driven decisions.
Let's look at an example of Bayesian statistics using PyMC4. We will see how to implement Bayesian linear regression.
import pymc as pm
import numpy as np
# Generate synthetic data
np.random.seed(42)
x = np.linspace(0, 1, 100)
true_intercept = 1
true_slope = 2
y = true_intercept + true_slope * x + np.random.normal(scale=0.5, size=len(x))
# Define the model
with pm.Model() as model:
# Priors for unknown model parameters
intercept = pm.Normal("intercept", mu=0, sigma=10)
slope = pm.Normal("slope", mu=0, sigma=10)
sigma = pm.HalfNormal("sigma", sigma=1)
# Likelihood (sampling distribution) of observations
mu = intercept + slope * x
likelihood = pm.Normal("y", mu=mu, sigma=sigma, observed=y)
# Inference
trace = pm.sample(2000, return_inferencedata=True)
# Summarize the results
print(pm.summary(trace))
Now, let us understand the above code step by step.
- Sets initial beliefs (priors) for the intercept, slope, and noise.
- Define a likelihood function based on these prior data and on the observed data.
- The code uses Markov chain Monte Carlo (MCMC) sampling to generate samples from the posterior distribution.
- Finally, the results are summarized to show the estimated parameter values and uncertainties.
Ending
Bayesian methods combine prior beliefs with new evidence to make informed decisions. They improve predictive accuracy and manage uncertainty across multiple domains. Tools such as PyMC4, Stan, and TensorFlow Probability provide strong support for Bayesian analysis. These tools help make probabilistic predictions from complex data.
Jayita Gulati She is a machine learning enthusiast and technical writer driven by her passion for building machine learning models. She holds a Masters in Computer Science from the University of Liverpool.






