Atroradores en los circuitos de la red neuronal: belleza y caos

¿Es una cosa en común entre los recuerdos, las reacciones químicas oscilantes y los péndulos dobles? Todos estos sistemas tienen una cuenca de atracción para posibles estados, como un imán que atrae el sistema hacia ciertas trayectorias. Los sistemas complejos con múltiples entradas generalmente evolucionan con el tiempo, generando comportamientos intrincados y a veces caóticos. Los atractores representan el patrón de comportamiento a largo plazo de los sistemas dinámicos, un patrón al que un sistema converge con el tiempo, independientemente de sus condiciones iniciales.

Las redes neuronales se han vuelto ubicuas en nuestra era actual de inteligencia artificial, que generalmente sirven como herramientas poderosas para la extracción de representación y el reconocimiento de patrones. Sin embargo, estos sistemas también se pueden ver a través de otra lente fascinante: como sistemas dinámicos que evolucionan y convergen a un colector de estados a lo largo del tiempo. Cuando se implementan con bucles de retroalimentación, incluso las redes neuronales simples pueden producir atractores sorprendentemente hermosos, que van desde ciclos límite hasta estructuras caóticas.

Redes neuronales como sistemas dinámicos

Si bien las redes neuronales en el sentido general son más conocidas por integrar tareas de extracción, también pueden verse como sistemas dinámicos. Un sistema dinámico describe cómo evolucionan los puntos en un espacio de estado con el tiempo de acuerdo con un conjunto fijo de reglas o fuerzas. En el contexto de las redes neuronales, el espacio estatal consiste en los patrones de activación de las neuronas, y la regla de evolución está determinada por los pesos, los sesgos, las funciones de activación y otros trucos de la red.

Los NN tradicionales se optimizan a través del descenso de gradiente para encontrar su estatal de convergencia. Sin embargo, cuando presentamos comentarios, conectando la salida a la entrada, la red se convierte en un sistema recurrente con un tipo diferente de dinámica temporal. Estas dinámicas pueden exhibir una amplia gama de comportamientos, desde convergencia simple hasta un punto fijo hasta patrones caóticos complejos.

Comprender los atractores

Un atractor es un conjunto de estados hacia los cuales un sistema tiende a evolucionar desde una amplia variedad de condiciones iniciales. Una vez que un sistema llega a un atractor, permanece dentro de ese conjunto de estados a menos que sea perturbado por una fuerza externa. De hecho, los atractores están profundamente involucrados en la formación de recuerdos (1), reacciones químicas oscilantes (2) y otros sistemas dinámicos no lineales.

Tipos de atractores

Los sistemas dinámicos pueden exhibir varios tipos de atractores, cada uno con características distintas:

• Punto Atractores: la forma más simple, donde el sistema converge a un solo punto fijo independientemente de las condiciones de inicio. Esto representa un estado de equilibrio estable.
• Ciclos límite: El sistema se establece en una órbita periódica repetida, formando un circuito cerrado en el espacio de fase. Esto representa el comportamiento oscilatorio con un período fijo.
• Toroidal Atroradores (cuasiperiódicos): el sistema sigue trayectorias que se enrolla alrededor de una estructura similar a la rosquilla en el espacio de fase. A diferencia de los ciclos límite, estas trayectorias nunca se repiten realmente, pero permanecen vinculadas a una región específica.
• Extraño Atroradores (caóticos): caracterizados por un comportamiento aperiódico que nunca se repite exactamente aún permanece limitado dentro de una región finita de espacio de fase. Estos atractores exhiben una dependencia sensible de las condiciones iniciales, donde una pequeña diferencia introducirá consecuencias significativas con el tiempo: un sello distintivo del caos. Piense en el efecto de la mariposa.

Configuración

En la siguiente sección, profundizaremos en un ejemplo de una arquitectura NN muy simple capaz de dicho comportamiento y demostraremos algunos ejemplos bonitos. Tocaremos los exponentes de Lyapunov y proporcionaremos implementación para aquellos que deseen experimentar con la generación de su propio arte de atractores de redes neuronales (y no en el sentido generativo de IA).

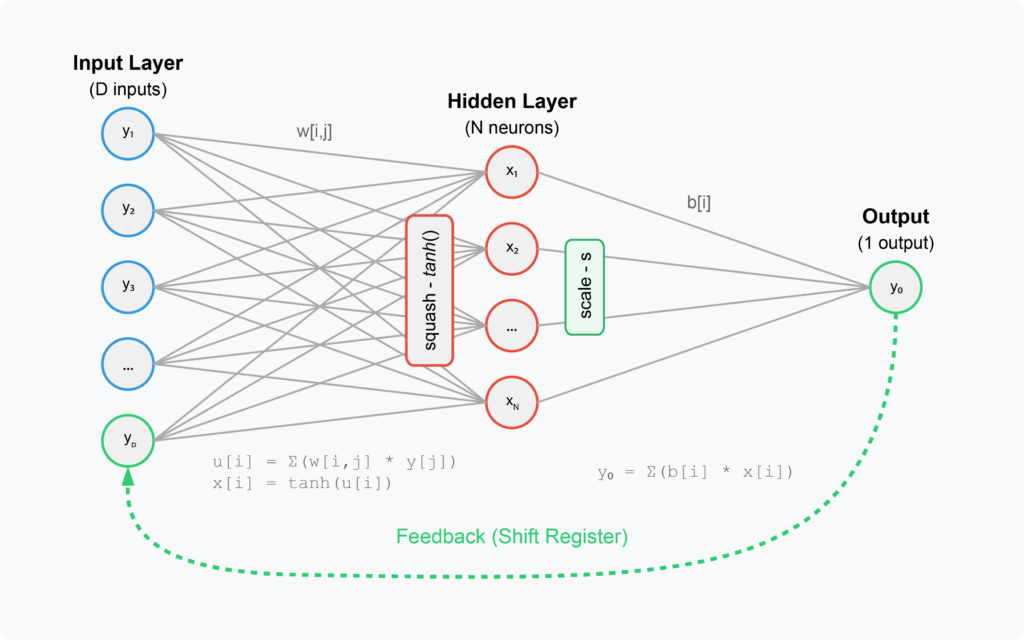
Usaremos un NN de una capa muy simplificado con un bucle de retroalimentación. La arquitectura consiste en:

1. Capa de entrada:
   • Matriz de entradas de tamaño D (aquí 16-32)
   • Los etiquetaremos no convencionalmente como y₁, y₂, y₃, …, y_D para resaltar que estos se asignan de las salidas
   • Actúa como un registro de turno que almacena salidas anteriores
2. Capa oculta:
   • Contiene N neuronas (aquí menos de D, ~ 4-8)
   • Los etiquetaremos x₁, x₂, …, x_norte
   • tanh() La activación se aplica para aplastar
3. Capa de salida
   • Neurona de salida única (y₀)
   • Combina las salidas de la capa oculta con sesgos, por lo general, usamos sesgos para compensar las salidas agregándolas; Aquí los usamos para escalar, por lo que son una variedad de pesas.
4. Conexión:
   • Entrada a Oculto: Matriz de peso W (I, J) (inicializado al azar entre -1 y 1)
   • Oculto a la salida: pesos de sesgo B (i) (inicializado aleatoriamente entre 0 y s)
5. Bucle de retroalimentación:
   • La salida Y₀ se vuelve a volver a la capa de entrada, creando un mapa dinámico
   • Actúa como un registro de turno (y₁ = anterior y₀, y₂ = anterior y₁, etc.)
   • Esta retroalimentación es lo que crea el comportamiento del sistema dinámico
6. Fórmulas clave:
   • Capa oculta: u (i) = σ (w (i, j) * y (j)); x (i) = tanh(u (i))
   • Salida: y₀ = σ (b (i) * x (i))

Los aspectos críticos que hacen que esta red genere atractores:

• El bucle de retroalimentación Convierte una red de Feedforward simple en un sistema dinámico
• El función de activación no lineal (tanh) habilita comportamientos complejos
• El Inicialización de peso aleatoria (controlado por la semilla aleatoria) crea diferentes patrones de atracción
• El factor de escala s afecta la dinámica del sistema y puede empujarlo a regímenes caóticos

Para investigar cuán propenso es el sistema al caos, calcularemos los exponentes de Lyapunov para diferentes conjuntos de parámetros. El exponente de Lyapunov es una medida del Inestabilidad de un sistema dinámico…

\ (delta z

\ (Lambda = n_t sum_ {k = 0}^{n_t-1} ln frac {| delta y_ {k+1} |} {| de telta y_k |} \)

… donde n_TSon una serie de pasos de tiempo, Δy_k Es una distancia entre los estados y (x_i) e y (x_i+ϵ) en un momento; Δz (0) representa una separación infinitesimal inicial (muy pequeña) entre dos puntos de partida cercanos, y Δz

¡Vamos a codificarlo! Solo usaremos bibliotecas Python Numpy y predeterminadas para la implementación.

import numpy as np
from typing import Tuple, List, Optional


class NeuralAttractor:
    """
    
    N : int
        Number of neurons in the hidden layer
    D : int
        Dimension of the input vector
    s : float
        Scaling factor for the output

    """
    
    def __init__(self, N: int = 4, D: int = 16, s: float = 0.75, seed: Optional(int) = 
None):
        self.N = N
        self.D = D
        self.s = s
        
        if seed is not None:
            np.random.seed(seed)
        
        # Initialize weights and biases
        self.w = 2.0 * np.random.random((N, D)) - 1.0  # Uniform in (-1, 1)
        self.b = s * np.random.random(N)  # Uniform in (0, s)
        
        # Initialize state vector structures
        self.x = np.zeros(N)  # Neuron states
        self.y = np.zeros(D)  # Input vector

Inicializamos el NeuralAttractor Clase con algunos parámetros básicos: número de neuronas en la capa oculta, número de elementos en la matriz de entrada, factor de escala para la salida y semilla aleatoria. Procedemos a inicializar los pesos y sesgos al azar, y los estados x e Y. Estos pesos y prejuicios no se optimizarán: se quedarán, sin descenso de gradiente esta vez.

    def reset(self, init_value: float = 0.001):
        """Reset the network state to initial conditions."""
        self.x = np.ones(self.N) * init_value
        self.y = np.zeros(self.D)
        
    def iterate(self) -> np.ndarray:
        """
        Perform one iteration of the network and return the neuron outputs.
        
        """
        # Calculate the output y0
        y0 = np.sum(self.b * self.x)
        
        # Shift the input vector
        self.y(1:) = self.y(:-1)
        self.y(0) = y0
        
        # Calculate the neuron inputs and apply activation fn
        for i in range(self.N):
            u = np.sum(self.w(i) * self.y)
            self.x(i) = np.tanh(u)
            
        return self.x.copy()

A continuación, definiremos la lógica de iteración. Comenzamos cada iteración con el bucle de retroalimentación: implementamos el circuito de registro de cambio cambiando todos los elementos Y hacia la derecha y calculamos la más reciente Y reciente₀ Salir para colocarlo en el primer elemento de la entrada.

    def generate_trajectory(self, tmax: int, discard: int = 0) -> Tuple(np.ndarray, 
np.ndarray):
        """
        Generate a trajectory of the states for tmax iterations.
        
        -----------
        tmax : int
            Total number of iterations
        discard : int
            Number of initial iterations to discard

        """
        self.reset()
        
        # Discard initial transient
        for _ in range(discard):
            self.iterate()
        
        x1_traj = np.zeros(tmax)
        x2_traj = np.zeros(tmax)
        
        for t in range(tmax):
            x = self.iterate()
            x1_traj
            x2_traj
            
        return x1_traj, x2_traj

Ahora, definimos la función que iterará nuestro mapa de red durante el número de pasos de tiempo TMAX y emitirá los estados de las dos primeras neuronas ocultas para la visualización. Podemos usar cualquier neuronas ocultas, e incluso podríamos visualizar el espacio de estado 3D, pero limitaremos nuestra imaginación a dos dimensiones.

Esta es la esencia del sistema. Ahora, solo definiremos algo de magia de línea y segmento para visualizaciones bonitas.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.collections as mcoll
import matplotlib.path as mpath
from typing import Tuple, Optional, Callable


def make_segments(x: np.ndarray, y: np.ndarray) -> np.ndarray:
    """
    Create list of line segments from x and y coordinates.
    
    -----------
    x : np.ndarray
        x coordinates
    y : np.ndarray
        Y coordinates

    """
    points = np.array((x, y)).T.reshape(-1, 1, 2)
    segments = np.concatenate((points(:-1), points(1:)), axis=1)
    return segments


def colorline(
    x: np.ndarray,
    y: np.ndarray,
    z: Optional(np.ndarray) = None,
    cmap = plt.get_cmap("jet"),
    norm = plt.Normalize(0.0, 1.0),
    linewidth: float = 1.0,
    alpha: float = 0.05,
    ax = None
):
    """
    Plot a colored line with coordinates x and y.
    
    -----------
    x : np.ndarray
        x coordinates
    y : np.ndarray
        Y coordinates

    """
    if ax is None:
        ax = plt.gca()
        
    if z is None:
        z = np.linspace(0.0, 1.0, len(x))
    
    segments = make_segments(x, y)
    lc = mcoll.LineCollection(
        segments, array=z, cmap=cmap, norm=norm, linewidth=linewidth, alpha=alpha
    )
    ax.add_collection(lc)
    
    return lc


def plot_attractor_trajectory(
    x: np.ndarray,
    y: np.ndarray,
    skip_value: int = 16,
    color_function: Optional(Callable) = None,
    cmap = plt.get_cmap("Spectral"),
    linewidth: float = 0.1,
    alpha: float = 0.1,
    figsize: Tuple(float, float) = (10, 10),
    interpolate_steps: int = 3,
    output_path: Optional(str) = None,
    dpi: int = 300,
    show: bool = True
):
    """
    Plot an attractor trajectory.
    
    Parameters:
    -----------
    x : np.ndarray
        x coordinates
    y : np.ndarray
        Y coordinates
    skip_value : int
        Number of points to skip for sparser plotting

    """
    fig, ax = plt.subplots(figsize=figsize)
    
    if interpolate_steps > 1:
        path = mpath.Path(np.column_stack((x, y)))
        verts = path.interpolated(steps=interpolate_steps).vertices
        x, y = verts(:, 0), verts(:, 1)
    
    x_plot = x(::skip_value)
    y_plot = y(::skip_value)
    
    if color_function is None:
        z = abs(np.sin(1.6 * y_plot + 0.4 * x_plot))
    else:
        z = color_function(x_plot, y_plot)
    
    colorline(x_plot, y_plot, z, cmap=cmap, linewidth=linewidth, alpha=alpha, ax=ax)
    
    ax.set_xlim(x.min(), x.max())
    ax.set_ylim(y.min(), y.max())
    
    ax.set_axis_off()
    ax.set_aspect('equal')
    
    plt.tight_layout()
    
    if output_path:
        fig.savefig(output_path, dpi=dpi, bbox_inches='tight')

    return fig

Las funciones escritas anteriormente tomarán las trayectorias de espacio de estado generadas y las visualizarán. Porque el espacio estatal puede estar densamente lleno, omita cada octavo, 16 o 32º punto para disfrazar nuestros vectores. Tampoco queremos trazarlos en un color sólido, por lo tanto estamos codificar el color como una función periódica (np.sin (1.6 * y_plot + 0.4 * x_plot)) basado en las coordenadas x e y del eje de la figura. Los multiplicadores para las coordenadas son arbitrarios y generan mapas de color lisos y agradables, para su gusto.

N = 4
D = 32
s = 0.22
seed=174658140

tmax = 100000
discard = 1000

nn = NeuralAttractor(N, D, s, seed=seed)

# Generate trajectory
x1, x2 = nn.generate_trajectory(tmax, discard)

plot_attractor_trajectory(
    x1, x2,
    output_path='trajectory.png',
)

Después de definir los parámetros NN y de iteración, podemos generar las trayectorias de espacio de estado. Si pasamos suficiente tiempo hurgando con parámetros, encontraremos algo genial (¡lo prometo!). Si el trabajo de búsqueda de la cuadrícula de parámetros manuales no es exactamente lo nuestro, podríamos agregar una función que verifique qué La proporción del espacio estatal se cubre con el tiempo. Si después de T = 100,000 iteraciones (excepto los 1,000 pasos de tiempo de “calentamiento” iniciales) solo tocamos un rango estrecho de valores del espacio de estado, es probable que estemos atrapados en un punto. Una vez que encontramos un atractor que no es tan tímido para ocupar más espacio de estado, podemos trazarlo utilizando parámetros de trazado predeterminados:

Uno de los tipos estables de atractores es el Atractor del ciclo límite (Parámetros: n = 4, d = 32, s = 0.22, semilla = 174658140). Parece una sola trayectoria de circuito cerrado en el espacio de fase. La órbita sigue una ruta regular y periódica en las series de tiempo. No incluiré el código para el cálculo del exponente de Lyapunov aquí para centrarme más en el aspecto visual de los atractores generados, pero uno puede encontrarlo bajo esto. enlacesi está interesado. El exponente de Lyapunov para este atractor (λ = −3.65) es negativo, lo que indica estabilidad: Matemáticamente, este exponente conducirá al estado del sistema en descomposición o convergente a esta cuenca de atracción a lo largo del tiempo.

Si seguimos aumentando el factor de escala, es más probable que ajustemos los valores en el circuito y quizás sea más probable que encuentre algo interesante.

Aquí está el atractor toroidal (cuasiperiódico) (Parámetros: n = 4, d = 32, s = 0.55, semilla = 3160697950). Todavía tiene una estructura ordenada de hojas que se envuelven en patrones cuasiperiódicos organizados. El exponente de Lyapunov para este atractor tiene un valor más alto, pero sigue siendo negativo (λ = −0.20).

A medida que aumentamos aún más los factores de escala S, el sistema se vuelve más propenso al caos. El Atractor extraño (caótico) Emerge con los siguientes parámetros: n = 4, d = 16, s = 1.4, semilla = 174658140). Se caracteriza por un patrón errático e impredecible de trayectorias que nunca se repiten. El exponente de Lyapunov para este atractor es positivo (λ = 0.32), lo que indica inestabilidad (divergencia de un estado inicialmente muy cercano a lo largo del tiempo) y el comportamiento caótico. Este es el atractor del “efecto de la mariposa”.

A medida que aumentamos aún más los factores de escala S, el sistema se vuelve más propenso al caos. El atractor extraño (caótico) emerge con los siguientes parámetros: n = 4, d = 16, s = 1.4, semilla = 174658140. Se caracteriza por un patrón errático e impredecible de trayectorias que nunca se repiten. El exponente de Lyapunov para este atractor es positivo (λ = 0.32), lo que indica inestabilidad (divergencia de un estado inicialmente muy cercano a lo largo del tiempo) y el comportamiento caótico. Este es el atractor del “efecto de la mariposa”.

Solo otra confirmación de que la estética puede ser muy matemática, y viceversa. Los atractores más convincentes a menudo existen en el borde del caos, ¡piense en ello por un segundo! Estas estructuras son lo suficientemente complejas como para exhibir un comportamiento complejo, pero ordenados lo suficiente como para mantener la coherencia. Esto resuena con observaciones de varias formas de arte, donde el equilibrio entre el orden y la imprevisibilidad a menudo crea las experiencias más atractivas.

Un widget interactivo para generar y visualizar estos atractores está disponible <a target="_blank" href="https://www.codehelix.ai/blog/attractors”>aquí. El código fuente es disponibletambién, e invita a una mayor exploración. Las ideas detrás de este proyecto se inspiraron en gran medida en el trabajo de JC Sprott (3).

Referencias

(1) B. Poucet y E. Save, Atractors in Memory (2005), Science Doi: 10.1126/science.1112555.

(2) YJF Kpomahou et al., Comportamientos caóticos y atractores coexistentes en un nuevo oscilador químico paramétrico disipativo no lineal (2022), complejidad Doi: 10.1155/2022/9350516.

(3) JC Sprott, Attres de red neuronal artificial (1998), computadoras y gráficos Dos: 10.1016/S0097-8493 (97) 00089-7.