He Quantum AI from Google team is building quantum computers with superconductor microwave circuitry, but just like a classic computer, the superconducting processor at the heart of these computers is only part of the story. An entire technology stack of peripheral hardware is required for the quantum computer to function properly. In many cases, these parts must be custom designed, requiring extensive research and development to achieve the highest levels of performance.
In this post, we highlight one aspect of this complementary hardware: our superconducting microwave amplifiers. In “Reading a quantum processor with high dynamic range Josephson parametric amplifiers“, published in Letters of Applied Physics, we describe how we increase the maximum output power of our superconducting microwave amplifiers by a factor of more than 100x. We discuss how this work may pave the way for the operation of larger quantum processor chips with improved performance.
Why microwave amplifiers?
One of the challenges of operating a superconducting quantum processor is measuring the state of a qubit without disturbing its operation. Fundamentally, this boils down to a microwave engineering problemwhere we need to be able to measure the energy inside the qubit resonator without exposing you to noisy or leaky cabling. This can be achieved by adding an additional microwave resonator to the system that is coupled to the qubit, but away from the qubit’s resonant frequency. The resonator acts as a filter that isolates the qubit from the control lines, but also captures a change in frequency dependent on the state of the qubit. Like in the binary phase shift keying encoding technique (BPSK), the digital state of the qubit (0 or 1) is translated into a phase for a probe tone (microwave signal) that is reflected by this auxiliary resonator. Measuring the phase of this probe tone allows us to infer the state of the qubit without directly interacting with the qubit itself.
While this sounds simple, the qubit actually imposes a severe limit on how much power can be used for this probe tone. In normal operation, a qubit must be in either state 0 or state 1, or some superposition of the two. A measurement pulse should collapse the qubit into one of these two states, but using too much energy can push it into a more excited state and corrupt the calculation. A safe measurement power is usually around -125 dBm, which is equivalent to only a handful of microwave photons interacting with the processor during the measurement. Small signals are usually measured with microwave amplifiers, which increase the level of the signal, but also add their own noise. How much noise is acceptable? If the measurement process takes too long, the state of the qubit may change due to loss of power in the circuit. This means that these very small signals must be measured in a few hundred nanoseconds with very high fidelity (>99%). Therefore, we cannot afford to average the signal over a longer time to reduce noise. Unfortunately, even the best semiconductor low noise amplifiers they are still almost a factor of 10 too loud.
The solution is to design our own custom amplifiers based on the same circuit elements as the qubits themselves. These amplifiers generally consist of josephson crosses to provide a tunable inductance connected to a superconducting resonant circuit. By building a resonant circuit out of these elements, you can create a parametric amplifier where amplification is achieved by modulating the tunable inductance at twice the frequency you want to amplify. Also, because all wiring is made of lossless superconductors, these devices operate near the aggregate noise quantum limit, where the only noise in the signal comes from amplification of zero-point quantum voltage fluctuations.
The only disadvantage of these devices is that the Josephson junctions limit the power of the signals that we can measure. If the signal is too large, the drive current can approach the critical junction current and degrade amplifier performance. Even if this limit were enough to measure a single qubit, our goal was to increase efficiency by measuring up to six qubits at a time with the same amplifier. Some groups circumvent this limit by making traveling wave amplifiers, where the signals are distributed in thousands of crossings. This increases the saturation power, but the amps become very complicated to produce and take up a lot of space on the chip. Our goal was to create an amplifier that could handle as much power as a traveling wave amplifier but with the same simple and compact design that we are used to.
Results
The critical current of each Josephson junction limits the power handling of our amplifier. However, increasing this critical current also changes the inductance and thus the operating frequency of the amplifier. To avoid these restrictions, we replace a SQUID CC standard 2-joint with a non-linear tunable inductor formed by two RF-SQUID arrays in parallel, what we call snake inducer. Each RF-SQUID consists of a Josephson junction and geometric inductors L1 and L2, and each array contains 20 RF-SQUIDs. In this case, each union of a pattern DC SQUID is replaced by one of these RF-SQUID arrays. While the critical current of each RF-SQUID is much higher, we chain them together to keep the inductance and operating frequency the same. While this is a relatively modest increase in device complexity, it allows us to increase the power handling of each amplifier by roughly a factor of 100x. It is also fully compatible with existing designs that use impedance matching circuits to provide a large measurement bandwidth.
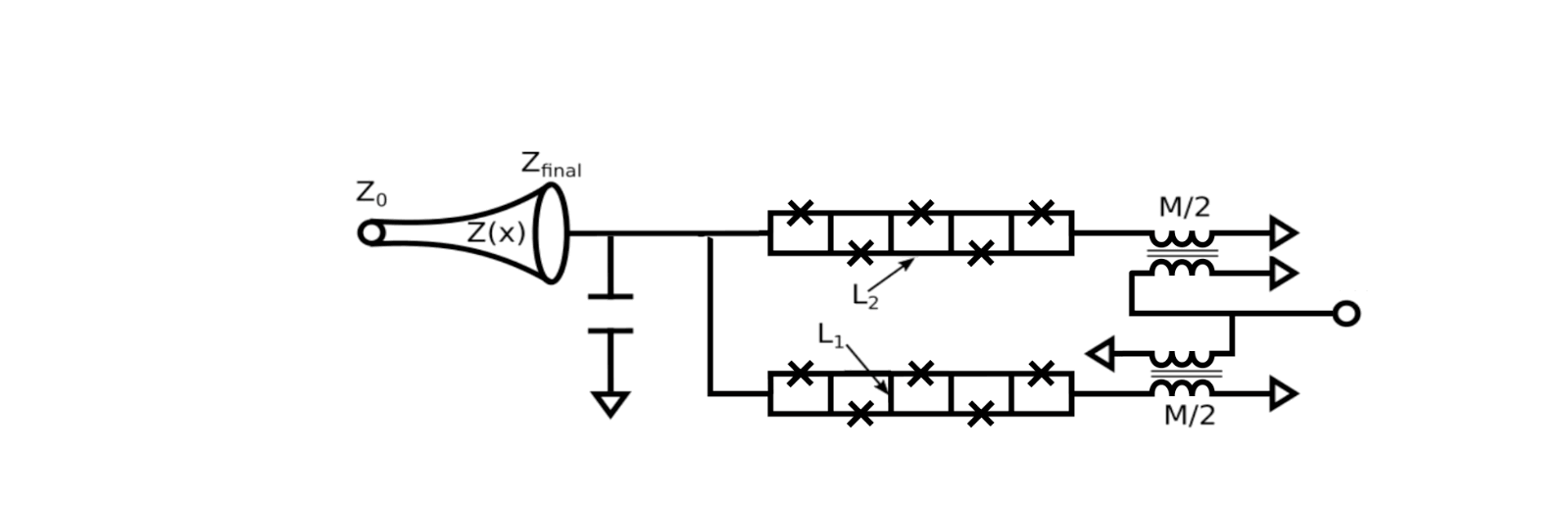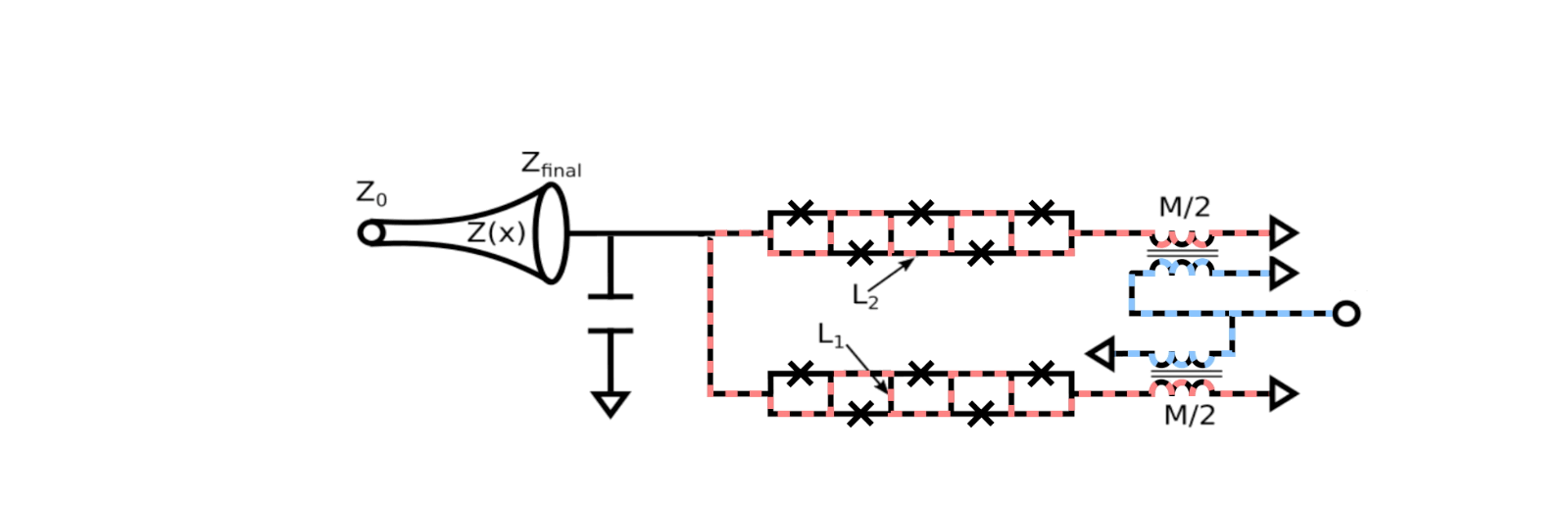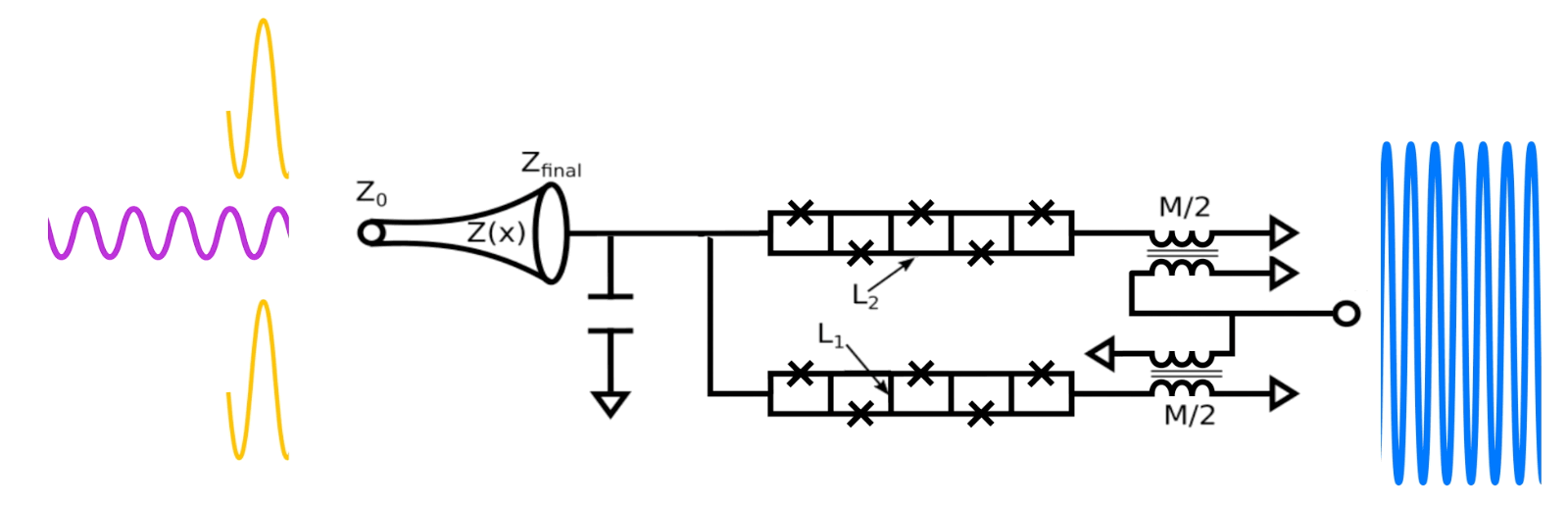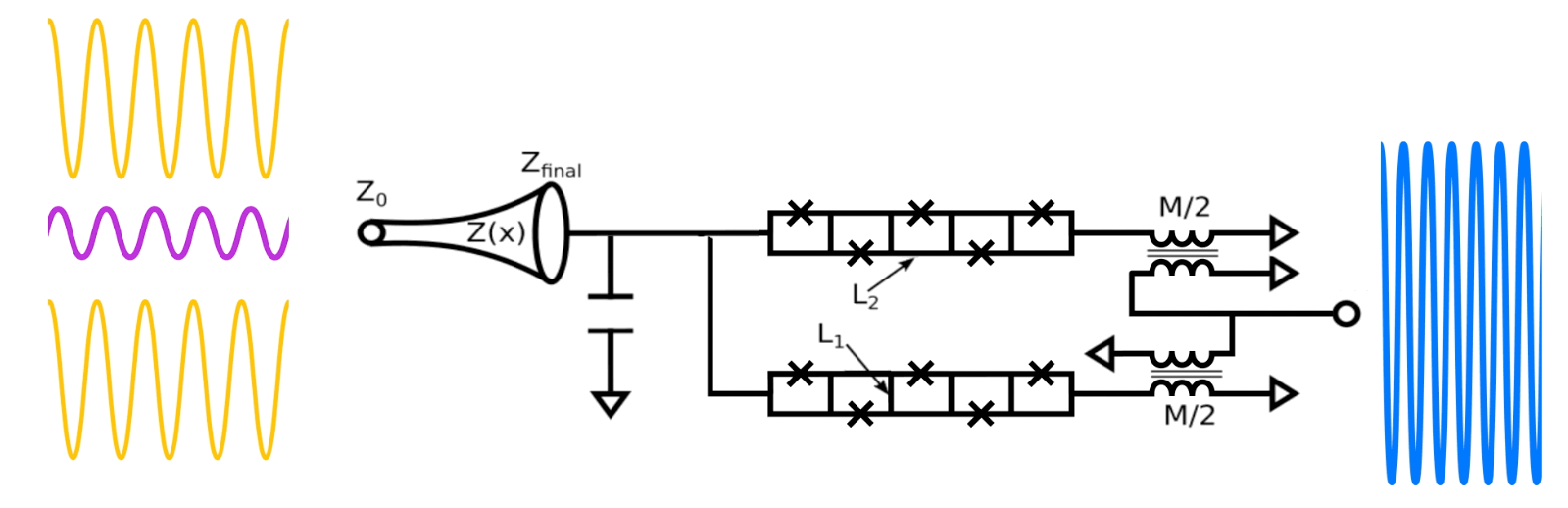 |
| Circuit diagram of our superconducting microwave amplifier. A part bias coil allows for DC and RF modulation of the snake inductor, while a bypass capacitor sets the frequency range. Current flow is illustrated in the animation where an applied current (blue) in the bias line causes a circulating current (red) in the snake. TO taper impedance transformer drop the load what of the device Since Q is defined as the frequency divided by the bandwidth, reducing Q with a constant frequency increases the bandwidth of the amplifier. Example circuit parameters used for a real device are Cs=6.0pF, L1=2.6pH, L2=8.0pH, Lb=30pH, M=50pH, Z0 = 50 ohmsand Zfinal = 18 ohms. The operation of the device is illustrated by a small signal (magenta) reflecting off the input of the amplifier. When the big bomb tone (blue) is applied to the bias port, it generates amplified versions of the signal (gold) and an secondary tone known as idle (also gold). |
We measure this improvement in performance by measuring the power saturation of the amplifier, or the point at which the gain is compressed by 1 dB. We also measure this power value against frequency to see how it scales with the amplifier’s gain and distance from the center of the amplifier’s bandwidth. Since the amplifier’s gain is symmetric about its center frequency, we measure this in terms of absolute detuning, which is simply the absolute value of the difference between the amplifier’s center frequency and the frequency of the probe tone.
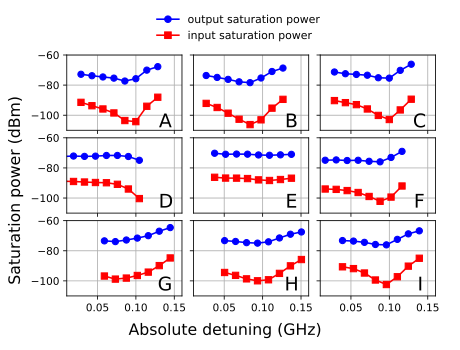 |
| Input and output saturation power (1 dB gain compression point), calibrated with a superconducting quantum processor against the absolute detuning of the amplifier’s center frequency. |
Conclusion and future directions
The new microwave amplifiers represent a huge step forward for our qubit measurement system. They will allow us to measure more qubits with a single device and will enable techniques that require higher power for each measurement tone. However, there are still quite a few areas that we would like to explore. For example, we are currently investigating the application of snake inductors in amplifiers with advanced impedance matching techniquesdirectional amplifiers and non-reciprocating devices such as microwave circulators.
Thanks
We would like to thank the Quantum AI team for the infrastructure and support that enabled the creation and measurement of our microwave amplifying devices. Thanks to our cohort of talented Google research interns who contributed to the future work mentioned above: Andrea Iorio for developing algorithms that automatically tune amplifiers and provide a snapshot of the local parameter space, Ryan Kaufman for measuring a new class of amplifiers using multipole impedance matching networks, and Randy Kwende for designing and testing a range of parametric devices based on snake inductors. With your contributions, we are gaining a better understanding of our amplifiers and designing the next generation of parametric devices.





