A handful of tricks concerning the sampling, architecture, activation function, loss balancing, optimisers, data normalisation, and more.
Physics-informed neural networks (PINNs) [1] have been gaining popularity in recent years for being continuous, fully differentiable models for solving partial differential equations (PDEs). They have the ability to solve complex problems in fields like engineering, science, finance, and many more. But as with any field of Machine Learning, there are startling challenges to overcome, for which there are no answers in the literature yet. In my work with PINNs, I have come across a variety of hurdles and have developed a set of hints and tricks to help improve their performance.
While these tricks are not exhaustive, they are based on empirical observations from working on diverse problems and have consistently resulted in improved performance. I want to share these insights with you, to help you in your journey with PINNs. This guide will hopefully provide you with practical suggestions to help improve your models and achieve better results.
As usual, these articles are accompanied by notebooks where you can directly try out the concepts introduced here:
Of course for any trick I found that improves the performance of my PINNs, there are several things I tried that did not work out. I listed these findings in an other article.
When designing PINN models, I usually opt for shallow but wide architectures. This means using fewer layers but having more nodes per layer. Networks with three to four layers of 256 nodes each have generally been enough to reach acceptable accuracy. There are a couple of theoretically motivated reasons that underpin my empirical observations:
- The shapes and patterns that PINNs need to capture are usually relatively simple compared to models in other fields of AI like natural language processing or semantic image segmentation. As a result, smaller networks should be sufficient to solve the task at hand. If the model fails to reach good accuracy, this may be a hint that there is an issue elsewhere in the pipeline, such as the problem definition or the sampling process.
- Every additional layer increases the likelihood of vanishing or exploding gradients. Since PINNs require several orders of differentiation instead of just one as in classical neural network optimisation, they are particularly prone to these pathologies.
- Recent results from automatic and differentiable architecture searches for PINNs suggest that shallow but wide networks tend to lead to better performance [3].
Selecting appropriate activation functions may sound straight-forward. However, activation functions take on an even more important role in PINNs than they do in classical neural networks. This is because the PINN’s outputs are derived multiple times with respect to the input and an additional time with respect to the model’s weights. It is crucial to ensure that the activation function is differentiable at least the same number of times before returning zero everywhere. Specifically, it should have n + 1 non-zero derivatives, where n is the order of differentiation in the PDE being solved. This is also the reason why the otherwise so popular ReLU activation can not be used in the context of PINNs: its first derivative is constant (either 0 or 1) and its second derivative zero everywhere (besides the non-defined zero point).
But even if an activation function has infinite differentiability in theory, the shape of each derivative is important for the modelling capability of the PINN at that specific order of differentiation. For example, if your problem involves approximating a particularly complex function at the kth order of differentiation, ensure that your activation function also has the appropriate shape at this order k.
In theory, using the sine as activation function may seem like the obvious choice in PINNs due to them retaining the same shape across all levels of differentiation. However, despite other claims [2], I have never been able to consistently make the sine activation function work in my projects.
What if there are two activation functions with desirable properties for your problem? You could either use one on one half of the nodes, and the other on the others, or you could linearly combine them into a single function.
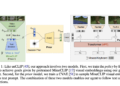
A more sophisticated method is to define two separate PINNs, each with its own activation function, and then aggregate their predictions. This can be done with the use of a gating network that weights each PINN’s contribution based on the input. There have been several studies on ensembles for PINNs, such as XPINNs or GatedPINNs. However, the version that has consistently worked best for me are MoE-PINNs (Mixture of Experts PINN) [3].
MoE-PINNs offer several advantages such as reduced complexity of the problem through the utilisation of multiple learners on distinct sub-domains, parallelizability by placing learners on different devices, and smaller dependence on costly hyperparameter tuning by initialising the ensemble with a large number of PINNs, each with different architectures, and a sparsity regularisation that takes care of reducing the importance of experts with sub-optimal properties.
PINNs learn from physical laws and are therefore usually self-supervised. Hence, when it comes to the dataset for training PINNs, we have the luxury of being able to choose which points we want to train our model on. The usual procedure is to uniformly sample points inside the domain as well as on each of the boundaries. The following points are important to keep in mind:
- Sample enough points on the boundaries. A good rule of thumb is to have the same cumulative number of points on the boundaries as inside the domain. But this proportion should be changed based on the complexity of each objective.
- Re-sample the points at each iteration. Randomly sampling points several times is a cheap operation. By doing it, you ensure that the entire domain is covered and ensure that localised features, like discontinuities, are better captured.
- Explore different sampling methods. Depending on your problem, sampling schemes like grid- or Sobol-sampling may be better suited than random sampling. An interesting approach could also be to sample more points where the error in the last iteration was highest [4].
Residual connections [5] have played an important role in the success of Convolutional Neural Networks because they improve the gradient flow during backpropagation and thus allow to build substantially deeper models with more layers. Training PINNs involves taking several higher-order derivatives. Due to numerical errors, each derivative makes the final gradients noisier. It is therefore important to facilitate the flow of gradients through the network. The shortcuts provided by residual connections are an elegant feature that helps achieving this.
The way these residual connections are implemented is a design choice. An interesting proposal in the context of PINNs is to use a multiplication instead of a sum [6].
L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) is a quasi-Newton method, meaning that it uses an approximation of the Hessian matrix to compute the gradient updates, rather than computing the exact Hessian matrix as in the Newton’s method. Unlike Adam, L-BFGS does not have a fixed learning rate, but instead, it adapts the learning rate at each iteration based on the approximation of the Hessian matrix. This makes it effective in reducing the PINN’s loss, especially in the later stages of training where other first order optimisation techniques like Adam tend to oscillate around the optimal solution.
However, L-BFGS has been reported to be prone to getting stuck in local minima. For mitigating this, a common approach is to start the training procedure with the Adam optimiser and, once the model has converged, to start a second training run with L-BFGS. This allows you to fine-tune the model and reduce the loss even further.
But how to select the optimal learning rate for the first training run using Adam? I usually start off with a large value, for example 0.1, start a training run and observe the evolution of the losses. If they oscillate a lot, then I continuously reduce the initial learning rate until the losses decrease at a consistent rate.
An extremely effective way of improving your PINN’s performance is by using the ReduceLROnPlateau callback, available both in TensorFlow and PyTorch. It allows to set a patience argument that defines how many training iterations without improvement are accepted before reducing the learning rate. The factor by which the learning rate is then reduced is another hyperparameter.
I have found that setting the patience to 3,000 training iterations and the factor to 0.1 works well, and these hyperparameters are not highly sensitive. Instead of spending time tuning them, I would therefore suggest to focus on more important hyperparameters, such as balancing the terms in the multi-objective loss function, as explained in the next section.
The losses in PINNs typically fall into the category of Multi-Objective Optimisation (MOO), as they are comprised of several terms: one for the governing equation and one for each boundary and initial condition. These terms may have different units of measurement, leading to imbalanced gradients that heavily favour the terms with the highest magnitude. In my experiments, it happened often that the terms for the boundary conditions were significantly smaller than the terms for the governing equations, leading to the model ignoring them and finding any other function fulfilling the governing equation, but not the one I intended.
Imbalanced losses in PINNs can stem from various sources, not limited to the magnitude difference between the terms alone. For instance, the choice of activation function, or the complexity of the functions being approximated by each term, can also contribute to imbalanced updates. To address these issues, each term in the loss function can be individually scaled, so as to achieve the desired balance between all the objectives.
By weighting each term with a scalar lambda, it is possible to control its contribution towards the total loss. These scaling factors are highly sensitive hyperparameters and should be carefully selected.
If you do not want to go through the trouble of manually tuning them, you can resort to one of the several proposed adaptive scaling methods, such as SoftAdapt [7], Learning Rate Annealing [6] or ReLoBRaLo [8].
Normalising or standardising data is standard practice in classical neural networks. However, it is not as straight forward in PINNs. Modifying the scales of the collocation points or even performing batch-wise calculations such as in BatchNormalisation breaks the physics with which PINNs are trained.
However, given that we know the extent of the physical domain that the PINN will be trained on, we can add a line to the start of the neural network that scales the inputs to a range between -1 and 1.
import tensorflow as tf
from tensorflow.keras.layers import Input, Concatenate, Densedef pinn_model(n_layers:int, n_nodes:int, activation:tf.keras.activations, x_range:tuple, y_range:tuple):
x = Input((1,), name=name+'_input_x')
y = Input((1,), name=name+'_input_y')
# normalize data between -1 and 1
x_norm = (x - x_range[0]) / (x_range[1] - x_range[0])
y_norm = (y - y_range[0]) / (y_range[1] - y_range[1])
xy = Concatenate()([x_norm, y_norm]) * 2 - 1
u = Dense(n_nodes, activation=activation, kernel_initializer='glorot_normal')(xy)
for i in range(1, n_layers):
u = Dense(n_nodes, activation=activation, kernel_initializer='glorot_normal')(u) + u
u = Dense(1, use_bias=False, kernel_initializer='glorot_normal')(u)
return tf.keras.Model([x, y], u)
By including the normalisation into the architecture, it is taken into account during the gradient calculation and is therefore a valid operation. The normalisation step ensures that the data being fed into the network is in a consistent range, making it easier for the model to manipulate and learn from the data, which will in turn considerably accelerate the PINN’s convergence.
If you have tried all the previous hints and tricks and your PINN is still not working, it is worth taking a look at the Modulus framework by NVIDIA [9]. Modulus is a framework for developing physics-ML models that includes a wide range of tools, architectures, balancing schemes, and other resources to help you optimise your PINN.
Even if you do not want to use the toolbox directly, it is still a great idea to take a look at the extensive documentation provided by Modulus. The documentation covers a vast range of topics related to PINNs and provides a comprehensive summary of the current state of the field.
[1] M. Raissi, P. Perdikaris, and G. E. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, Journal of Computational Physics 378 (2019), 686–707.
[2] V. Sitzmann, J. N. Martel, A. Bergman, D. Lindell, and G. Wetzstein, “Implicit Neural Representations with Periodic Activation Functions,” arXiv e-prints, Jun. 2020, arXiv:2006.09661.
[3] R. Bischof and M. A. Kraus, “Mixture-of-Experts-Ensemble Meta-Learning for Physics-Informed Neural Networks”, Proceedings of 33. Forum Bauinformatik, 2022
[4] Z. Gao, L. Yan, and T. Zhou, “Failure-informed adaptive sampling for PINNs,” arXiv e-prints, Oct. 2022, arXiv:2210.00279.
[5] K. He, X. Zhang, S. Ren, and J. Sun, “Deep Residual Learning for Image Recognition,” arXiv e-prints, Dec. 2015, arXiv:1512.03385.
[6] Wang, S., Teng, Y., and Perdikaris, P. Understanding and mitigating gradient pathologies in physics-informed neural networks. arXiv e-prints (Jan. 2020), arXiv:2001.04536.
[7] Heydari, A. A., Thompson, C. A., and Mehmood, A. SoftAdapt: Techniques for Adaptive Loss Weighting of Neural Networks with Multi-Part Loss Functions. arXiv e-prints (Dec. 2019), arXiv:1912.12355.
[8] Rafael Bischof and Michael Kraus. Multi-objective loss balancing for physics-informed deep learning. arXiv preprint arXiv:2110.09813, 2021.
[9] O. Hennigh, S. Narasimhan, M. A. Nabian, A. Subramaniam, K. Tangsali, M. Rietmann, J. del Aguila Ferrandis, W. Byeon, Z. Fang, and S. Choudhry, “NVIDIA SimNetTM: an AI-accelerated multi-physics simulation framework,” arXiv e-prints, 2020.
 NEWSLETTER
NEWSLETTER