Merkle trees are a fundamental part of what makes blockchains work. While it’s definitely theoretically possible to make a Merkle-treeless blockchain, simply by creating giant block headers that directly contain each transaction, this poses major scalability challenges that possibly put the ability to use trustless blockchains out of everyone’s reach. except for the majority. powerful computers in the long run. Thanks to Merkle Trees, it is possible to build Ethereum nodes that run on all large and small computers and laptops, smartphones, and even Internet of Things devices like the ones you will produce. slock.it. So how exactly do these Merkle trees work and what value do they provide, both now and in the future?
First, the basics. A Merkle tree, in the most general sense, is a way of combining a large number of “chunks” of data that relies on dividing the chunks into buckets, where each bucket contains only a few chunks, and then taking the hash of each cube. and repeating the same process, continuing to do so until the total number of hashes remaining becomes one: the root hash.
The most common and simplest form of Merkle tree is the binary Mekle tree, where a bucket always consists of two adjacent shards or hashes; can be represented as follows:
So what is the benefit of this strange type of hash algorithm? Why not just concatenate all the chunks into one big chunk and use a regular hash algorithm on that? The answer is that it allows for an ordered mechanism known as Merkle tests:
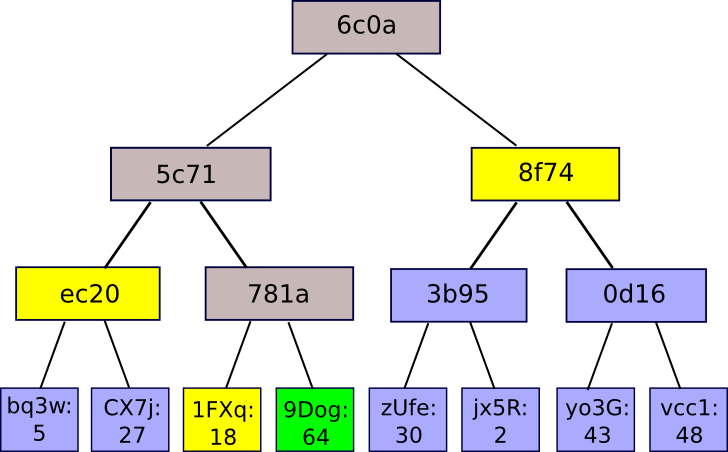
A Merkle proof consists of a shard, the root hash of the tree, and the “branch” consisting of all the hashes that go up along the path from the shard to the root. Someone reading the test can verify that the hash, at least for that branch, is consistent throughout the tree, and therefore that the given chunk really is at that position in the tree. The implementation is simple: Suppose there is a large database and all the content of the database is stored in a Merkle tree where the root of the Merkle tree is publicly known and trusted (for example, it was digitally signed by enough reliable parts). , or there are many tests working on it). So a user who wants to do a key-value lookup in the database (for example, “tell me the object at position 85273”) can request a Merkle proof, and upon receipt of the proof, verify that it is correct and , therefore, that the value received it really is at position 85273 in the database with that particular root. Allows a mechanism to authenticate a little amount of data, such as a hash, that will be extended to authenticate as well long databases of potentially unlimited size.
Merkle tests on Bitcoin
The original application of Merkle proofs was in Bitcoin, as described and created by Satoshi Nakamoto in 2009. The Bitcoin blockchain uses Merkle proofs to store the transactions in each block:
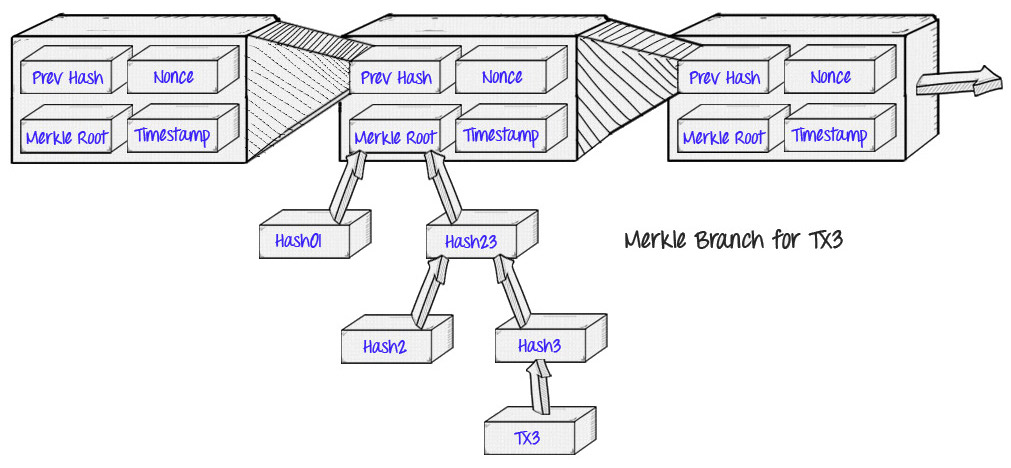
The benefit of this is the concept that Satoshi described as “simplified payment verification”: instead of downloading everyone transaction and each block, a “thin client” can only download the chain of block headers80-byte chunks of data for each block containing just five things:
- A hash of the previous header
- a timestamp
- A mining difficulty value
- A nonce proof of work
- A root hash for the Merkle tree that contains the transactions for that block.
If the thin client wants to determine the status of a transaction, it can simply request a Merkle proof showing that a particular transaction is in one of the Merkle trees rooted in a block header for the mainchain.
This gets us pretty far, but Bitcoin-style thin clients have their limitations. One particular limitation is that while they can prove the inclusion of transactions, they cannot prove anything about the current state (eg digital asset holdings, name registrations, the state of financial contracts, etc.). How many bitcoins do you have right now? A Bitcoin light client can use a protocol that involves querying multiple nodes and trusting that at least one of them will notify you of any particular transaction fees from their addresses, and this will get you pretty far for that use case, but for other more complex applications. is not sufficient; the precise nature of the effect of a transaction may depend on the effect of several previous transactions, which in turn depend on previous transactions, so ultimately you would have to authenticate every transaction in the entire chain. To avoid this, Ethereum takes the concept of the Merkle tree a step further.
Merkle tests on Ethereum
Each block header on Ethereum contains not only a Merkle tree, but Three trees for three types of objects:
- Proceedings
- Receipts (essentially, pieces of data that show the effect of each transaction)
- Express
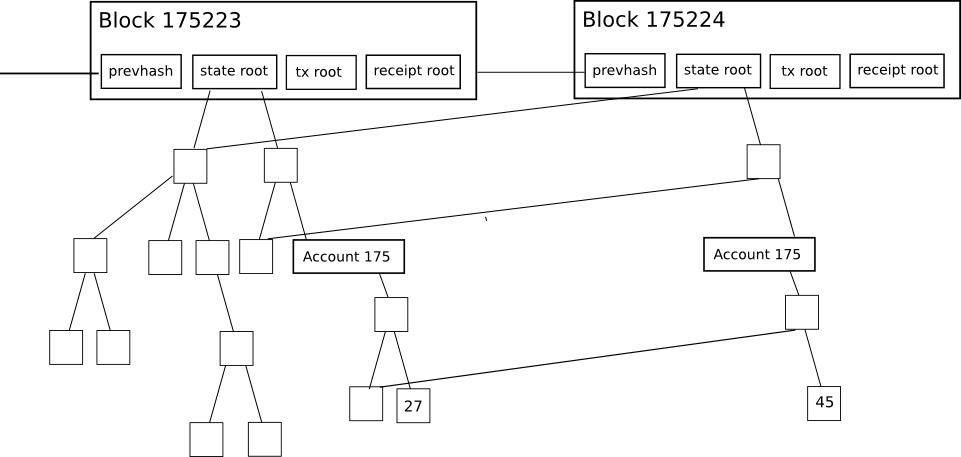
This enables a highly advanced thin client protocol that allows thin clients to easily make and get verifiable responses to many types of queries:
- Has this transaction been included in a particular block?
- Tell me all instances of an event of type X (for example, a crowdfunding contract reaching its goal) emitted by this address in the last 30 days
- What is the current balance of my account?
- Does this account exist?
- You intend to execute this transaction on this contract. What would be the output?
The first is handled by the transaction tree; the third and fourth are handled by the state tree and the second by the receipt tree. The first four are fairly easy to calculate; the server simply finds the object, looks up the Merkle branch (the list of hashes from the object to the root of the tree), and replies to the thin client with the branch.
The fifth is also handled by the state tree, but the way it is calculated is more complex. Here, we need to build what can be called a Merkle state transition test. Essentially, it’s a test that makes the claim “if you execute the transaction you in the rooted state Sthe result will be a rooted state YesWith registration L and exit EITHER” (“output” exists as a concept in Ethereum because each transaction is a function call; it’s not theoretically necessary.)
To compute the proof, the server locally creates a fake block, sets the state to S, and pretends to be a thin client while applying the transaction. That is, if the transaction application process requires the client to determine the balance of an account, the light client performs a balance query. If the thin client needs to check a particular item in storage for a particular contract, the thin client makes a query for that, and so on. The server correctly “responds” to all of its own queries, but keeps track of all the data it returns. The server then sends the combined data from all these requests to the client as evidence. The client then performs exactly the same procedure, but using the provided test as your database; if its result is the same as what the server claims, then the client accepts the proof.
patrician trees
It was mentioned earlier that the simplest type of Merkle tree is the binary Merkle tree; however, the trees used in Ethereum are more complex: this is the “Merkle Patricia tree” you hear about in our documentation. This item will not go into the detailed specification; that is best done by This article Y Thisalthough I will discuss the basic reasoning.
Merkle binary trees are very good data structures for authenticating information that is in “list” format; essentially, a series of fragments one after another. For transaction trees, they are also good because no matter how long it takes Edit a tree once it is created, as the tree is created once and then frozen forever.
For the state tree, however, the situation is more complex. State in Ethereum essentially consists of a key-value map, where the keys are addresses and the values are account statements, listing the balance, nonce, code, and storage for each account (where the storage is itself a tree). For example, the genesis state of Morden’s testnet looks like this:
{
"0000000000000000000000000000000000000001": {
"balance": "1"
},
"0000000000000000000000000000000000000002": {
"balance": "1"
},
"0000000000000000000000000000000000000003": {
"balance": "1"
},
"0000000000000000000000000000000000000004": {
"balance": "1"
},
"102e61f5d8f9bc71d0ad4a084df4e65e05ce0e1c": {
"balance": "1606938044258990275541962092341162602522202993782792835301376"
}
}
Unlike transaction history, however, the status must be updated frequently: account balance and nonce are often changed, and new accounts are frequently inserted and stored keys are frequently inserted and deleted. Therefore, what is desired is a data structure in which we can quickly compute the new root of the tree after an insert, update, edit, or delete operation, without recalculating the entire tree. There are also two highly desirable secondary properties:
- The depth of the tree is limited, even if an attacker is deliberately crafting transactions to make the tree as deep as possible. Otherwise, an attacker could perform a denial of service attack by manipulating the tree to be so deep that each individual update becomes extremely slow.
- The root of the tree depends solely on the data, not the order in which the updates are made. Doing updates in a different order and even recalculating the tree from scratch shouldn’t change the root.
He patricia tree, in simple terms, is perhaps the closest we can get to achieving all of these properties simultaneously. The simplest explanation of how it works is that the key under which a value is stored is hard-coded in the “path” that you should remove from the tree. Each node has 16 children, so the path is determined by the hex encoding: for example, the key dog hex encoded is 6 4 6 15 6 7, so it would start with the root, work its way down to the sixth child, then the fourth, and so on until it reached the end. In practice, there are some additional optimizations we can do to make the process much more efficient when the tree is sparse, but that’s the basic principle. Both articles mentioned on describe all the features in much more detail.
 NEWSLETTER
NEWSLETTER





