The basis of bitcoin's self-sovereignty is having control over its private keys. Without this, in one way or another, you are giving up control of your money to someone else. “Not your keys, not your coins,” as the saying goes. A counterintuitive aspect of bitcoin for people unfamiliar with its technical underpinnings is “where” your bitcoin actually is. When people think of a wallet, they think of “the place where I keep my money.” crypto/what-is-a-bitcoin-wallet-and-how-does-it-work”>Your bitcoin wallet It doesn't actually “hold” your bitcoin, it just stores your private keys. Your bitcoin are just data entries into the blockchain hosted by everyone participating in the network. When you go to spend your bitcoins, what you are actually doing is proposing an update to the data stored in the blockchain. A private key is the protocol's way of ensuring that you, and only you, can authorize an update to the blockchain that spends your bitcoin.
So what are your private keys? Just very large numbers. Extremely long. This is a private key in binary:
11100010110110010111101111000001010001000000100010011110101110110101011101110011111111111110101011101001011101001110100 111001 0100110111101000110000111110101111001101001011110011011101000001101101101110001101000110001111010001001001111011010101 0110011 01101010
256 random 1s and 0s. This random number is what ultimately protects your bitcoin. It may not seem like much, but its randomness is what ensures the safety of your wallet. There are almost as many possible bitcoin private keys as there are atoms in the visible universe. That's how many numbers a computer would have to count to generate and catalog all potentially possible private keys. As long as the process used to generate the keys is truly random, your keys will be safe.
This is what a private key looks like in hexadecimal (binary uses two digits to encode a number, 1 and 0, hexadecimal uses 16 digits, 0-9 and AF):
E2D97BC144089EBB5773FFABA5D3A729BD187D79A5E6E836DC68C7A24F6AB36A
This is what a private key looks like in uncompressed Wallet Import Format (WIF):
5KYC9aMMSDWGJciYRtwY3mNpeTn91BLagdjzJ4k4RQmdhQvE98G
The WIF format is how everyone interacted with their private keys in the early days of bitcoin. In this era, you could generate one private key at a time and then generate the public key from there. The process of generating a public key is essentially just the multiplication of very large numbers, but there is more to it than that. All public keys are x and y points on a graph that shows a very curve, very great curve that returns on itself.
On the graphic curve, in the case of bitcoin bitcoin.it/wiki/Secp256k1″>Secp256k1, there is a point called “generator point”. This generating point can be considered the “base point” of the Secp256k1 curve. It is an integral part of the process of generating keys and signing with them. This is the generating point of the bitcoin curve:
G=02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
To generate the public key from your private key, you take the private key you generated and multiply it by the generating point. That's all. This now sets a point on the graph with a mathematical relationship to the private key you generated and is known only to you.
This is an uncompressed public key showing the x and y points:
04C0E410A572C880D1A2106AFE1C6EA2F67830ABCC8BBDF24729F7BF3AFEA06158F0C04D7335D051A92442330A50B8C37CE0EC5AFC4FFEAB41732DA5108261FFED
It is very common to “zip” public keys in the rare case that you interact with them to simply store the x coordinate with a byte to tell you whether the y coordinate is negative or positive. That shortens it considerably:
04C0E410A572C880D1A2106AFE1C6EA2F67830ABCC8BBDF24729F7BF3AFEA06158F0C04D7335D051A92442330A50B8C37CE0EC5AFC4FFEAB41732DA5108261FFED
When you go to sign a transaction with your private key, it once again essentially boils down to simple multiplication. By generating a random number (the nonce) and using it along with your private key to essentially multiply the hash of the transaction you are signing, you produce the signature (which is made up of two values, r and S). This allows someone to run an algorithm to verify that the message was signed with the appropriate private key without revealing that key. What ensures that only you can authorize the spending of your bitcoin is essentially the multiplication of very, very large numbers.
If you're not very familiar with these concepts before reading this, all of this will probably seem a little intimidating. Binary? Hexadecimal? Chart points? How do you back up a WIF?
Since more intuitive ways to handle this data were developed, most users are not familiar with these complicated formats. Chances are you have more experience with word seeds, also known as seed phrases.
BIP 39 Mnemonic Seeds
Mnemonic seeds, or seed phrases, were created to address the problem of the experience of interacting with your private keys.
As we discussed above, private keys are ultimately just a long series of ones and zeros that are generated randomly. Imagine trying to create copies of this and making sure you don't make a mistake when transcribing it:
11100010110110010111101111000001010001000000100010011110101110110101011101110011111111111110101011101001011101001110100 111001 0100110111101000110000111110101111001101001011110011011101000001101101101110001101000110001111010001001001111011010101 0110011 01101010
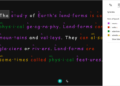
All it would take is a single mistake when copying a digit to render a backup of your keys useless. This is where mnemonic seeds come in handy. 256 consecutive 1s and 0s in a row is not a human-friendly way to interact with sensitive information. Registering this number incorrectly means losing access to your account.
truck renew fury donkey remember laptop reform detail divide sorrow because fat
It's much easier to deal with that, isn't it? Only 12 words. So how does that work, going from a bunch of random 1s and 0s to a string of words that actually make sense to you? An encoding scheme, such as binary or hexadecimal!
Each of those 12 words in that mnemonic seed above is a binary number in a coding scheme map specific strings of ones and zeros to words. If we look back at the previous example of the WIF private key, that was simply a number encoded in a specific encoding scheme, in that case base 58, which uses all the numbers and letters of the alphabet except 0 and 1, and O and l ( case sensitive). The exclusion of those characters was done specifically to make transcription errors unlikely by confusing a 1 with an O or a 0 with an O. bech32 and bech32m used by Segwit and Taproot take this to the next level by using only this character set (qpzry9x8gf2tvdw0s3jn54khce6mua7l).
bitcoin Improvement Proposal 39 (BIP 39) introduced a standardized encoding scheme in which each word in a specially designed dictionary is mapped alphabetically to a binary number from 00000000001 to 11111111111. The demo seed above maps to this:
truck: 11101001001
renew: 10110110001
fury: 01011110011
donkey: 01000001001
remember: 10110101110
laptop: 01111101000
reform: 10110100010
detail: 00111100010
split: 11010010001
penalty: 01100110100
because: 00010011110
fat: 01010011011
In binary it looks like this:
11101001001 10110110001 01011110011 01000001001 10110101110 01111101000 10110100010 00111100010 11010010001 01100110100 000 10011110 0101001 1011
There are 2048 words, each mapped to a specific 11-digit string of 1s and 0s, specifically to make it easier for people to interact with your private keys. When you generate a random number for your private key, your wallet cuts that number into 11-digit binary number chunks and maps them to the BIP 39 mnemonic dictionary. It's still the same big number, but now you can read it as English words. Since your brain is much more accustomed to this format than long strings of ones and zeros, this drastically reduces the chances of you typing the wrong thing and losing your bitcoin in the process.
You may have noticed that in the raw binary encoding of the seed word above, there are four independent digits (1011), and the last “word” is actually only 8 digits long. This is a checksum to ensure that a seed phrase is valid. When you generate your random number, there are not enough digits to assign it to exactly 12 (or 24) words. The wallet processes the existing digits it generated and takes the first few digits of the hash to add to the end of your random number. This gives you enough digits to assign to the last word.
This last word allows you to perform a security check on copies of your seed. If you incorrectly enter your mnemonic seed into a wallet, the checksum will not match. Each 12 or 24 word seed has multiple potentially valid checksum words, but if the last word does not match the checksum of a correct seed, your wallet will warn you that it is invalid. This gives people an intuitive but still mathematical way to ensure their backups are correct, as opposed to the complicated process of transcribing and backing up raw binary numbers.
Selecting specific words from the list even went so far as to ensure that none of the 2,048 words have the same first four letters. This was done to reduce the likelihood of people making transcription errors by confusing similar words and ending up with an incorrect backup of their private keys.
Translating these words into a place multiple private/public keys is pretty simple. Your mnemonic seed is taken and hashed using SHA512, which generates a hash of 512 individual 1s and 0s. Half of that output is used as an actual private key and the other half is used as input to SHA512 with an index number and the existing public or private key to generate a new key pair. You can do this as many times as you like to generate new public/private keys that can be retrieved from your single mnemonic phrase.
This ensures that you can manage your private keys with the same ease and No danger, as possible with the least chance of making a mistake that causes you to lose your money. And all of this was done using math! Hopefully, you now have a good understanding of why people say bitcoin is “mathematics-secured” money.