Image by author
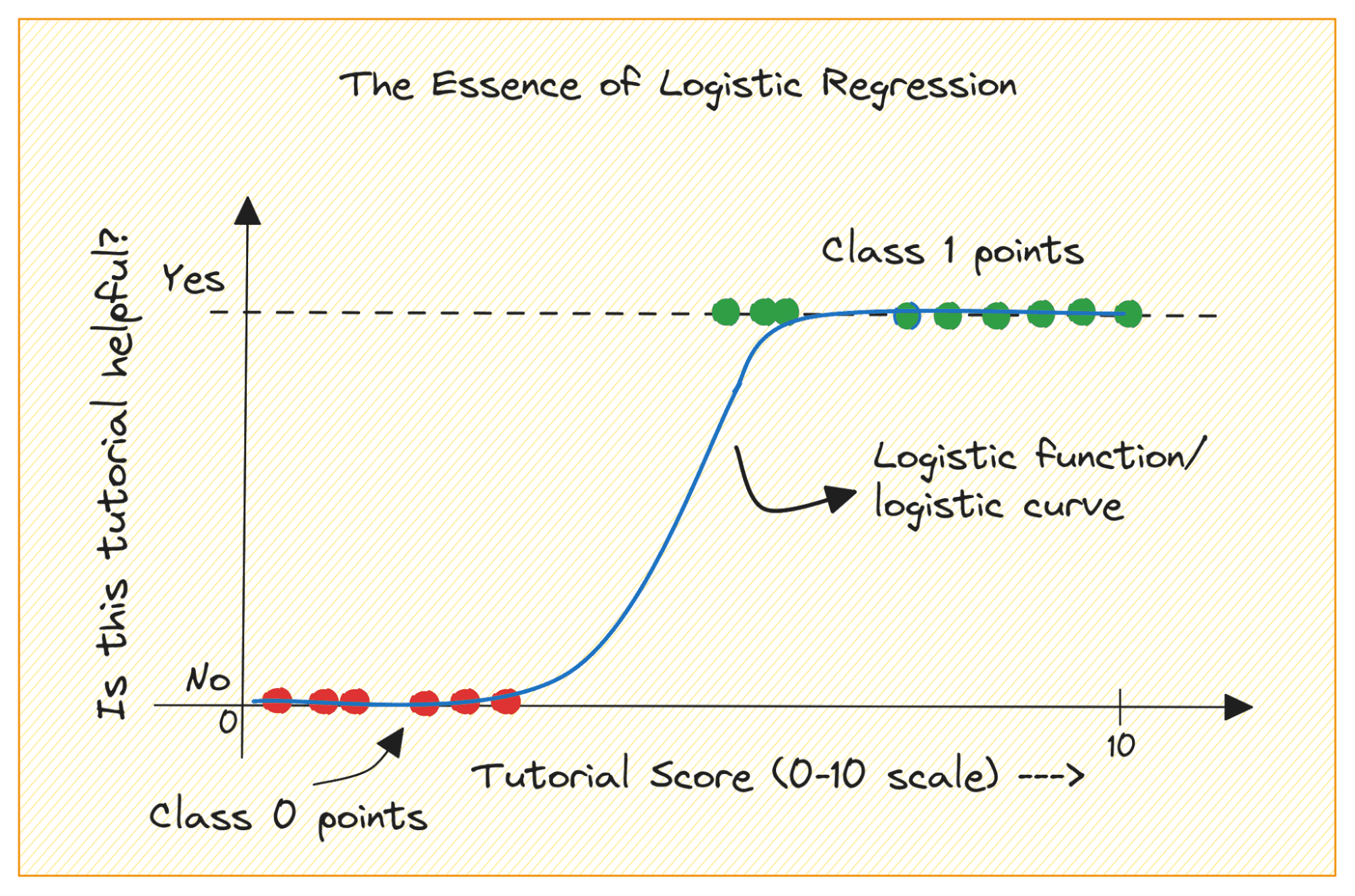
When you get started with machine learning, logistic regression is one of the first algorithms you'll add to your toolbox. It is a simple and robust algorithm, commonly used for binary classification tasks.
Consider a binary classification problem with classes 0 and 1. Logistic regression fits a logistic or sigmoid function to the input data and predicts the probability that a query data point belongs to class 1. Interesting, right?
In this tutorial, we will learn about logistic regression from scratch and cover:
- The logistic (or sigmoid) function
- How we go from linear to logistic regression
- How logistic regression works
Finally, we will build a simple logistic regression model to classify RADAR returns from the ionosphere.
Before learning more about logistic regression, let's review how the logistic function works. The logistic (or sigmoid) function is given by:


When you plot the sigmoid function, it will look like this:
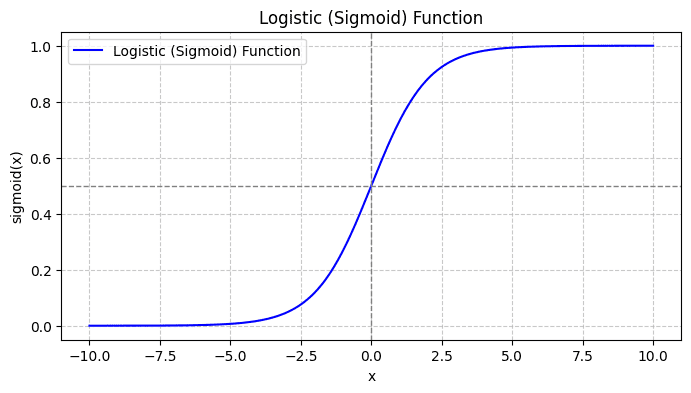

From the plot we see that:
- When x = 0, σ(x) takes a value of 0.5.
- As x approaches +∞, σ(x) approaches 1.
- As x approaches -∞, σ(x) approaches 0.
So for all real inputs, the sigmoid function squashes them to take values in the range (0, 1).
Let's first discuss why we cannot use linear regression for a binary classification problem.
In a binary classification problem, the result is a categorical label (0 or 1). Because linear regression predicts outcomes with continuous values that can be less than 0 or greater than 1, it does not make sense for the problem at hand.
Additionally, a straight line may not be the best choice when the output labels fall into one of the two categories.
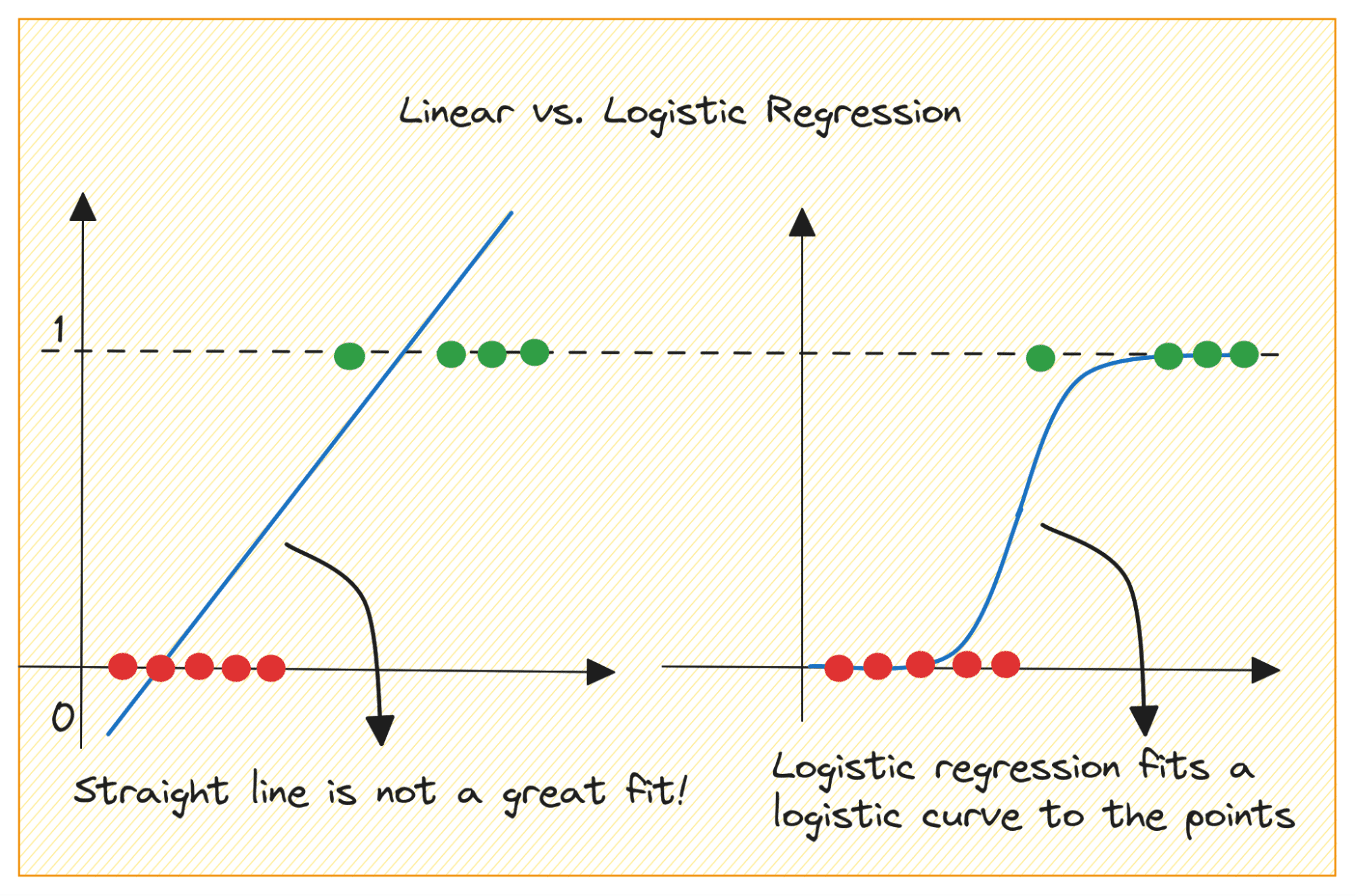

Image by author
So how do we go from linear to logistic regression? In linear regression, the predicted result is given by:
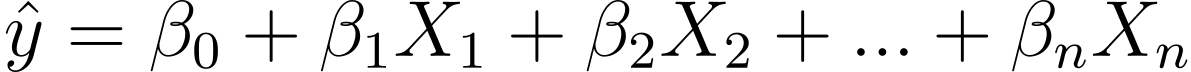
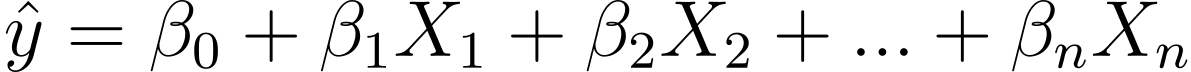
Where the β are the coefficients and X_is are the predictors (or characteristics).
Without loss of generality, suppose X_0 = 1:


So we can have a more concise expression:
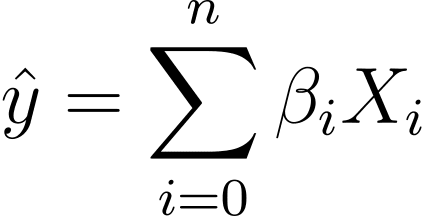
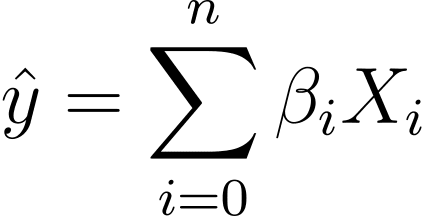
In logistic regression, we need the predicted probability p_i in the interval (0,1). We know that the logistic function squashes the inputs so that they take values in the interval (0,1).
So, plugging this expression into the logistic function, we have the predicted probability as:
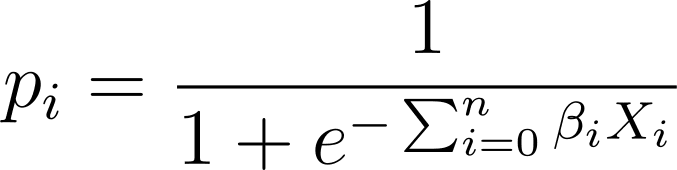
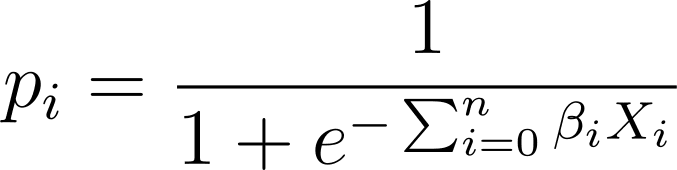
So how do we find the logistic curve that best fits the given data set? To answer this, let's understand maximum likelihood estimation.
Maximum Likelihood Estimation (MLE) It is used to estimate the parameters of the logistic regression model by maximizing the likelihood function. Let's discuss the process of MLE in logistic regression and how the cost function is formulated for optimization using gradient descent.
Maximum Likelihood Estimation Breakdown
As discussed, we model the probability of a binary outcome occurring as a function of one or more predictor variables (or characteristics):
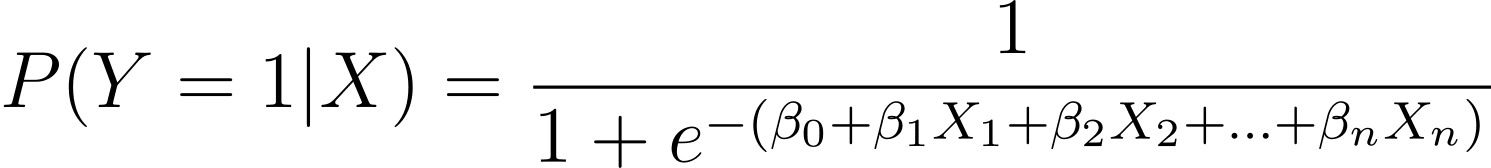
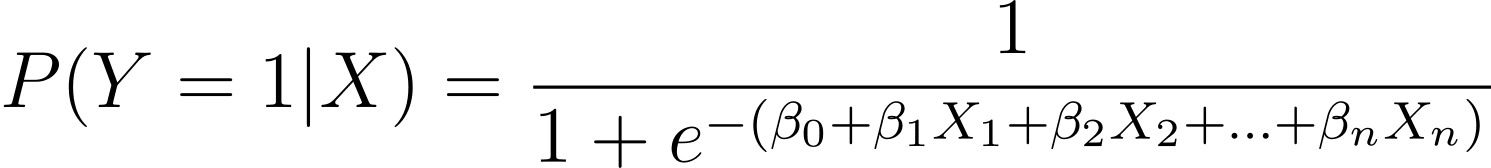
Here, the β are the parameters or coefficients of the model. X_1, X_2,…, X_n are the predictor variables.
MLE aims to find the values of β that maximize the probability of the observed data. The likelihood function, denoted as L(β), represents the probability of observing the given results for the given predictive values under the logistic regression model.
Formulation of the log-likelihood function
To simplify the optimization process, it is common to work with the log likelihood function. Because it transforms products of probabilities into sums of logarithmic probabilities.
The log likelihood function for logistic regression is given by:
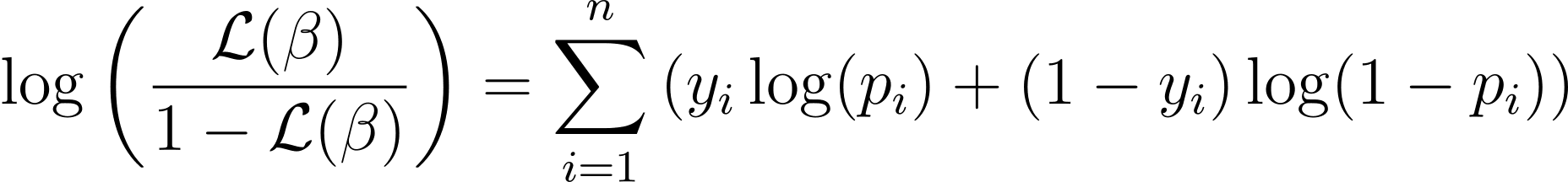
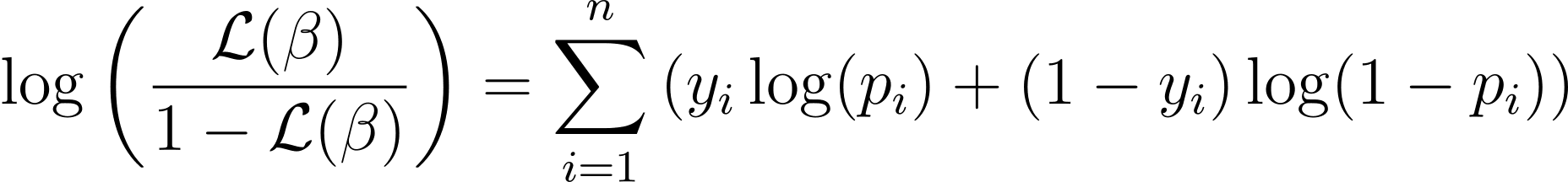
Now that we know the essence of log likelihood, let's proceed to formulate the cost function for logistic regression and subsequently gradient descent to find the best model parameters.
Cost function for logistic regression
To optimize the logistic regression model, we need to maximize the log likelihood. Therefore, we can use negative log likelihood as a cost function to minimize during training. Negative log likelihood, often called logistic loss, is defined as:
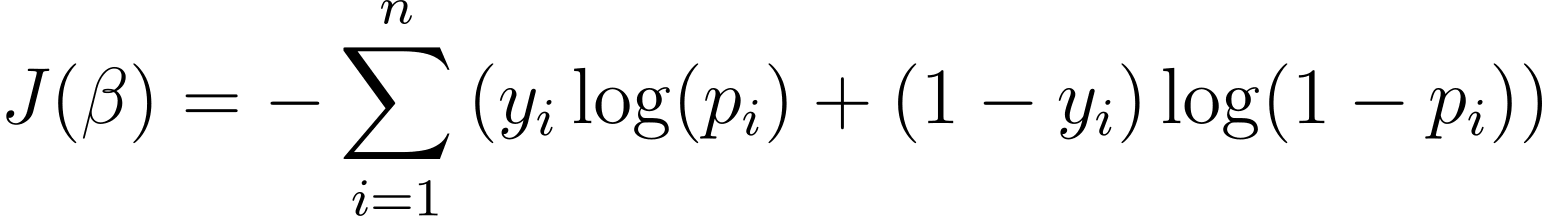
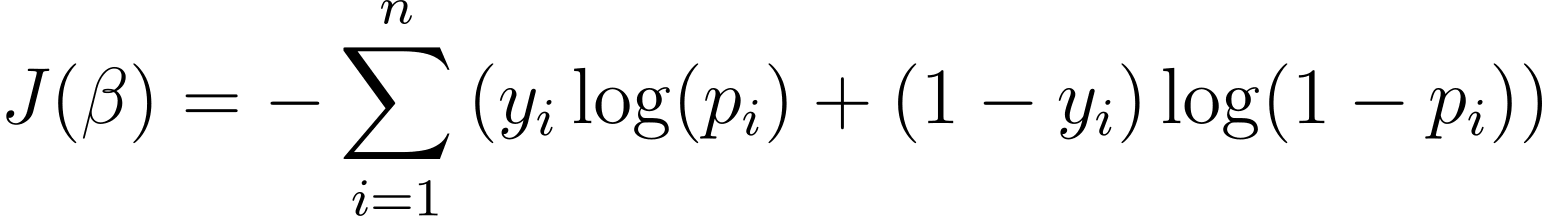
Therefore, the goal of the learning algorithm is to find the values of ? that minimize this cost function. Gradient descent is a commonly used optimization algorithm to find the minimum of this cost function.
Gradient descent in logistic regression
gradient descent is an iterative optimization algorithm that updates the model parameters β in the opposite direction to the gradient of the cost function with respect to β. The update rule at step t+1 for logistic regression using gradient descent is as follows:
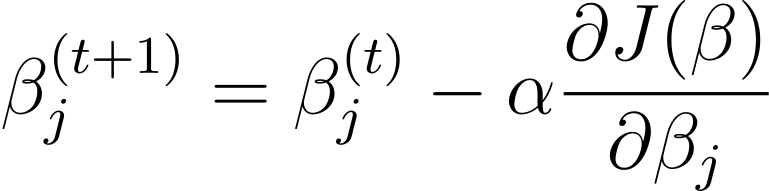
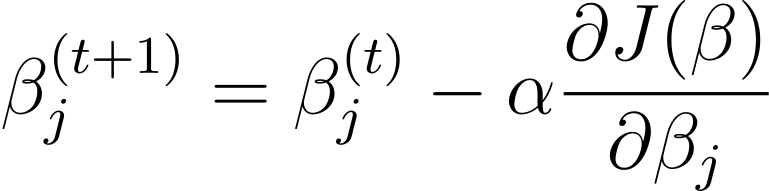
Where α is the learning rate.
Partial derivatives can be calculated using the chain rule. Gradient descent iteratively updates the parameters, until convergence, with the goal of minimizing logistic loss. As it converges, it finds the optimal values of β that maximize the probability of the observed data.
Now that you know how logistic regression works, let's create a predictive model using the scikit-learn library.
We will use the UCI Machine Learning Repository Ionosphere Dataset. for this tutorial. The data set comprises 34 numerical features. The output is binary, one of “good” or “bad” (denoted by “g” or “b”). The output label “good” refers to RADAR returns that have detected some structure in the ionosphere.
Step 1: Load the dataset
First, download the dataset and read it into a pandas dataframe:
import pandas as pd
import urllib
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/ionosphere/iphere.data"
data = urllib.request.urlopen(url)
df = pd.read_csv(data, header=None)Step 2: Explore the data set
Let's take a look at the first few rows of the data frame:
# Display the first few rows of the DataFrame
df.head()

Truncated output of df.head()
Let's get information about the data set: the number of non-null values and the data types of each of the columns:
# Get information about the dataset
print(df.info())
 Truncated output of df.info()
Truncated output of df.info()
Because we have all the numerical characteristics, we can also obtain some descriptive statistics using the describe() method in data frame:
# Get descriptive statistics of the dataset
print(df.describe())

Truncated output of df.describe()
Column names currently range from 0 to 34, including the label. Because the data set does not provide friendly names for the columns, it simply refers to them as attribute_1 through attribute_34. If you want, you can rename the data frame columns as shown:
column_names = (
"attribute_1", "attribute_2", "attribute_3", "attribute_4", "attribute_5",
"attribute_6", "attribute_7", "attribute_8", "attribute_9", "attribute_10",
"attribute_11", "attribute_12", "attribute_13", "attribute_14", "attribute_15",
"attribute_16", "attribute_17", "attribute_18", "attribute_19", "attribute_20",
"attribute_21", "attribute_22", "attribute_23", "attribute_24", "attribute_25",
"attribute_26", "attribute_27", "attribute_28", "attribute_29", "attribute_30",
"attribute_31", "attribute_32", "attribute_33", "attribute_34", "class_label"
)
df.columns = column_namesNote: This step is purely optional. You can continue with the default column names if you prefer.
# Display the first few rows of the DataFrame
df.head()

Truncated output of df.head() (after renaming columns)
Step 3: Rename class labels and view class distribution
Because the output class labels are 'g' and 'b', we must assign them to 1 and 0, respectively. You can do it using map() either replace():
# Convert the class labels from 'g' and 'b' to 1 and 0, respectively
df("class_label") = df("class_label").replace({'g': 1, 'b': 0})Let's also visualize the distribution of class labels:
import matplotlib.pyplot as plt
# Count the number of data points in each class
class_counts = df('class_label').value_counts()
# Create a bar plot to visualize the class distribution
plt.bar(class_counts.index, class_counts.values)
plt.xlabel('Class Label')
plt.ylabel('Count')
plt.xticks(class_counts.index)
plt.title('Class Distribution')
plt.show()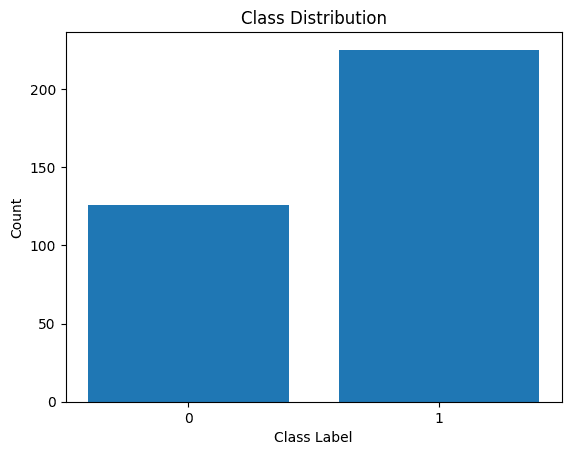

Class Label Distribution
We see that there is an imbalance in the distribution. There are more records that belong to class 1 than class 0. We will handle this class imbalance when building the logistic regression model.
Step 5: Preprocessing the Dataset
Let's collect the features and output tags like this:
X = df.drop('class_label', axis=1) # Input features
y = df('class_label') # Target variableAfter dividing the data set into training and testing sets, we need to preprocess the data set.
When there are many numerical features, each on a potentially different scale, we need to preprocess the numerical features. A common method is to transform them so that they follow a distribution with zero mean and unit variance.
He StandardScaler of scikit-learn's preprocessing module helps us achieve this.
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Get the indices of the numerical features
numerical_feature_indices = list(range(34)) # Assuming the numerical features are in columns 0 to 33
# Initialize the StandardScaler
scaler = StandardScaler()
# Normalize the numerical features in the training set
X_train.iloc(:, numerical_feature_indices) = scaler.fit_transform(X_train.iloc(:, numerical_feature_indices))
# Normalize the numerical features in the test set using the trained scaler from the training set
X_test.iloc(:, numerical_feature_indices) = scaler.transform(X_test.iloc(:, numerical_feature_indices))Step 6: Building a logistic regression model
Now we can instantiate a logistic regression classifier. He LogisticRegression The class is part of scikit-learn's linear_model module.
Notice that we have configured the class_weight parameter to 'balanced'. This will help us explain the class imbalance. Assigning weights to each class, inversely proportional to the number of records in the classes.
After creating an instance of the class, we can fit the model to the training data set:
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(class_weight="balanced")
model.fit(X_train, y_train)Step 7: Evaluation of the logistic regression model
You can call predict() Method to obtain model predictions.
In addition to the precision score, we can also get a ranking report with metrics such as precision, recall, and F1 score.
from sklearn.metrics import accuracy_score, classification_report
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
classification_rep = classification_report(y_test, y_pred)
print("Classification Report:\n", classification_rep) 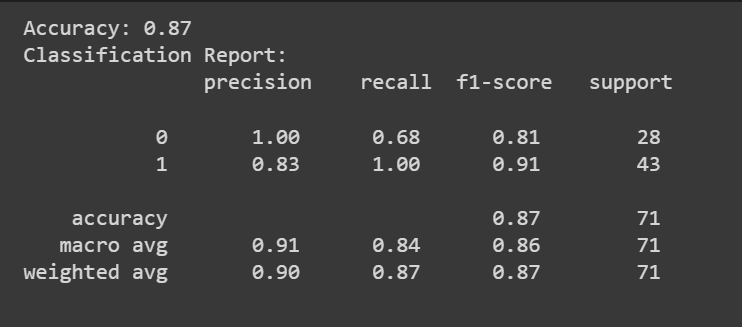

Congratulations, you have coded your first logistic regression model!
In this tutorial, we learned in detail about logistic regression: from theory and mathematics to coding a logistic regression classifier.
As a next step, try creating a logistic regression model for a suitable data set of your choice.
The Ionosphere dataset is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0):
Sigillito, V., Wing, S., Hutton, L. and Baker, K. (1989). Ionosphere. UCI Machine Learning Repository. https://doi.org/10.24432/C5W01B.
Bala Priya C. is a developer and technical writer from India. He enjoys working at the intersection of mathematics, programming, data science, and content creation. His areas of interest and expertise include DevOps, data science, and natural language processing. He likes to read, write, code and drink coffee! Currently, he is working to learn and share his knowledge with the developer community by creating tutorials, how-to guides, opinion pieces, and more.





