Neural networks learn through numbers, so each word will map to vectors to represent a particular word. The embedding layer can be thought of as a lookup table that stores word embeddings and retrieves them using indices.
Words that have the same meaning will be close in terms of Euclidean distance/cosine similarity. For example, in the word representation below, “Saturday,” “Sunday,” and “Monday” are associated with the same concept, so we can see that the words are turning out to be similar.

Determining the position of the word, why do we need to determine the position of the word? Because the transformer encoder does not have recursion like recurrent neural networks, we need to add information about the positions in the input embeddings. This is done using positional encoding. The authors of the article used the following functions to model the position of a word.
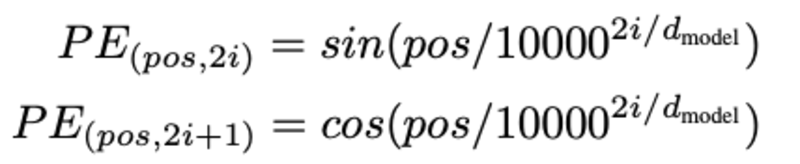
We will try to explain positional coding.
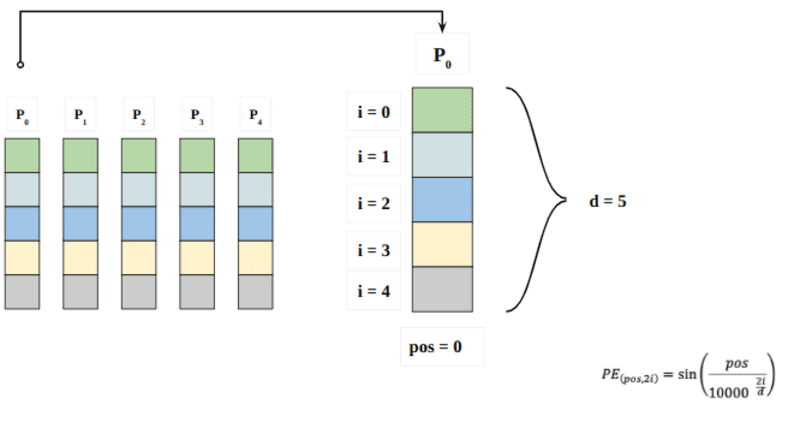
Here “pos” refers to the position of the “word” in the sequence. P0 refers to the embedding position of the first word; “d” means the size of the word/token embedding. In this example d=5. Finally, “i” refers to each of the 5 individual dimensions of the embedding (ie 0,1,2,3,4)
if “i” varies in the above equation, you’ll get a bunch of curves with varying frequencies. Reading the position embedding values against different frequencies, giving different values at different embedding dimensions for P0 and P4.
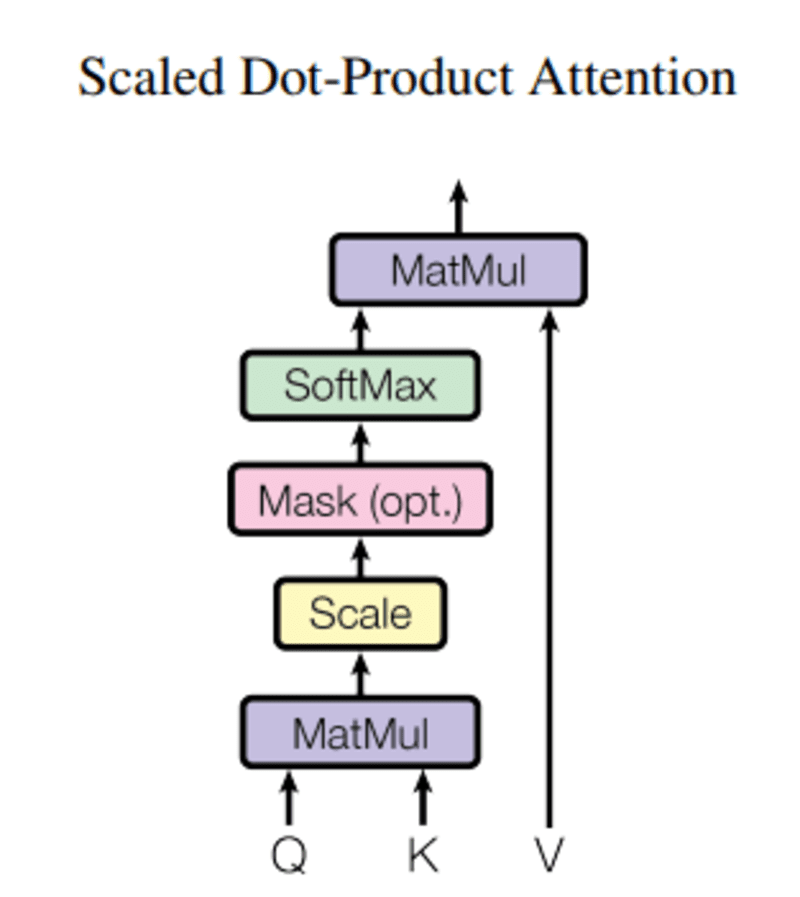
In this query, what represents a vector word, the k-keys are all the other words in the sentence, and V-value represents the word vector.
The purpose of attention is to calculate the importance of the key term compared to the query term related to the same person/thing or concept.
In our case, V is equal to Q.
The attention mechanism gives us the importance of the word in a sentence.
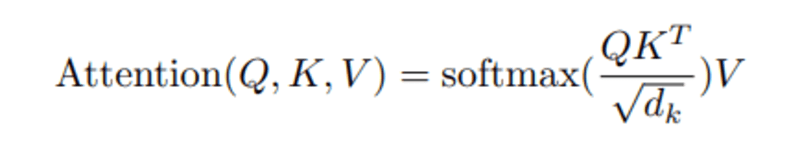
When we calculate the normalized dot product between the query and the keys, we get a tensor that represents the relative importance of each word for the query.
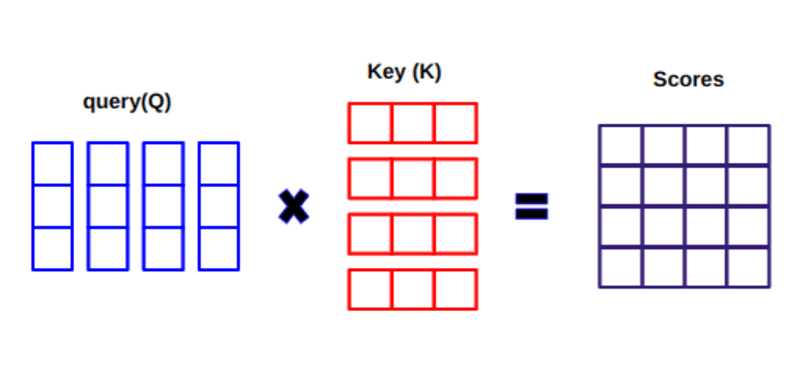
When calculating the dot product between Q and KT, we try to estimate how the vectors (ie, the words between the query and the keys) align, and return a weight for each word in the sentence.
We then normalize the result to the square of d_k and the softmax function regularizes the terms and rescales them between 0 and 1.
Finally, we multiply the result (ie weights) by the value (ie all words) to reduce the importance of non-relevant words and focus only on the most important words.
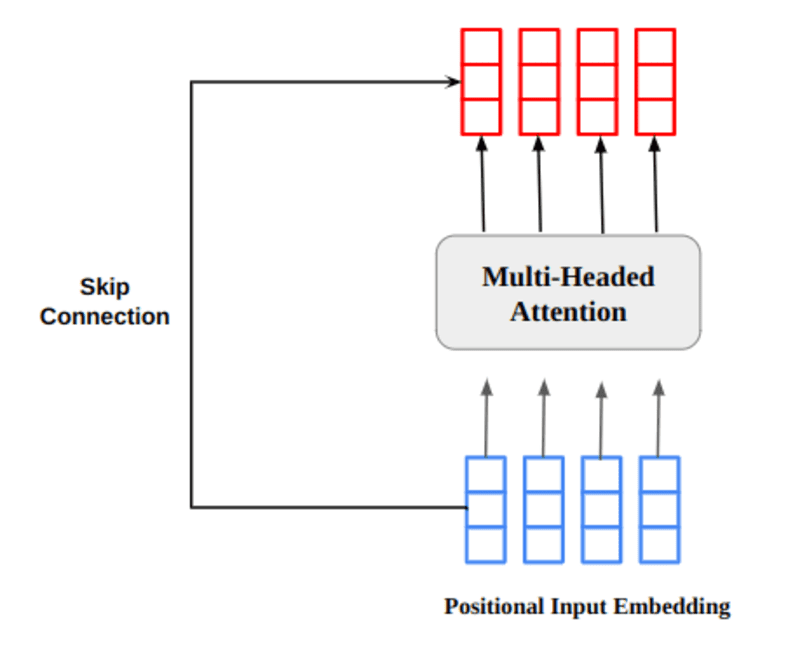
The multi-headed attention output vector is added to the original positional input embedding. This is called a residual connection/hop connection. The output of the residual connection goes through layer normalization. The normalized residual output is passed through a point forward feed network for further processing.
The mask is an array the same size as the attention scores filled with values of 0 and negative infinities.
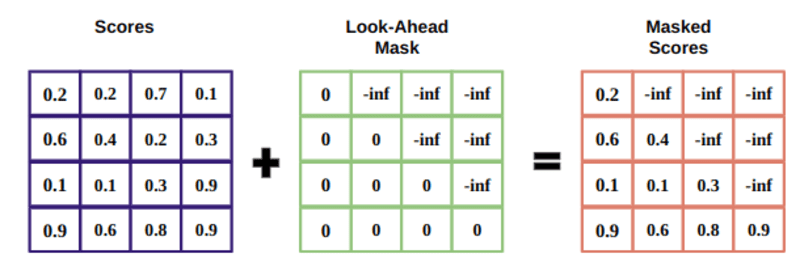
The reason for the mask is that once you take the softmax of the masked scores, the negative infinities become zero, leaving zero attention scores for future tokens.
This tells the model not to focus on those words.
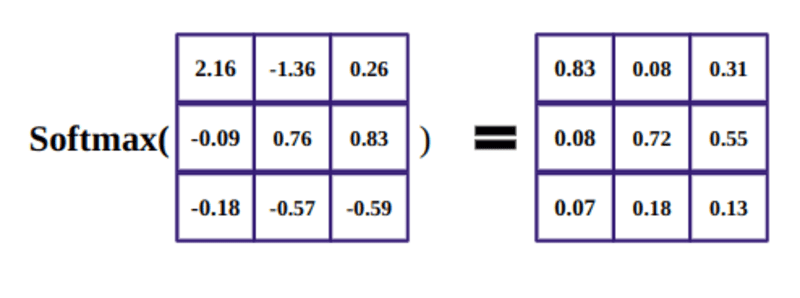
The purpose of the softmax function is to take real numbers (positive and negative) and convert them to positive numbers that sum to 1.
Ravikumar Naduvin you are busy building and understanding NLP tasks using PyTorch.
Original. Reposted with permission.





