Broadcast models have recently achieved cutting-edge results in content generation, including images, videos, and music. In this article, researchers at VISTEC in Thailand focus on speeding up the sampling time of diffusion models, allowing the sampling procedure to be conditioned to generate examples that belong to a specific class (such as “dog” or “cat”). ) or that are conditioned by an arbitrary notice. The authors investigate numerical methods used to solve differential equations to speed up the process of sampling guided diffusion models. These have already been used in unconditional diffusion models, but the authors show that integrating them into guided diffusion models is challenging. Therefore, they propose to consider more specific integration schemes based on the idea of “carrier splitting”.
In the landscape of generative models, diffusion models belong to probability-based methods such as stream normalization or variational autoencoders, since they are trained by maximizing a lower bound on the probability of the data and offer a stable training framework compared to generative antagonistic (GAN) approaches, while still delivering close performance. They can be described via a Markov chain that we would like to invert: Starting from a high-dimensional point of the data distribution, an initial point is degraded by iteratively adding Gaussian perturbations (a type of coding procedure). The generative process consists of learning a denoising decoder that inverts those disturbances. The overall process is highly computationally expensive, since it involves many iterations. In this article, the authors focus on the generative procedure by which the forward pass can be interpreted as the solution of a differential equation. The equation associated with the guided diffusion of the paper has the following form:
The right-hand side is the diffusion term, while the second term can be understood as a penalty term that imposes a gradient climb on the conditional distribution. Take the trajectory to a region of high density corresponding to the conditional density f. The authors emphasize that the direct application of a higher-order numerical integration scheme (eg, Runge-Kutta 4 or Pseudo Linear Multi-Step 4) fails to speed up the sampling procedure. Instead, they propose to use a division method. Division methods are commonly used to solve differential equations that involve different operators. For example, the simulation of ocean pollution by a chemical substance can be described by advection-diffusion equations: using a split method, we can separately treat the transport of this pollution (advection) and then apply a diffusion operator . This is the type of method that the authors propose to consider in this paper by “splitting” the above ODE in two to develop the above equation from time t to time t+1.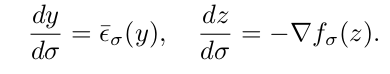
Among the existing splitting methods, the authors compare two different ones: the Lie-Trotter Splitting method and the Strang Splitting method. For each division method, they investigate different number schemes. His experiments involve text and class conditional generative tasks, superresolution, and unpainting. Their results support their claims: the authors show that they can reproduce samples to the same quality as the baseline (which uses a 250-step integration scheme) using 32-58% less sampling time.
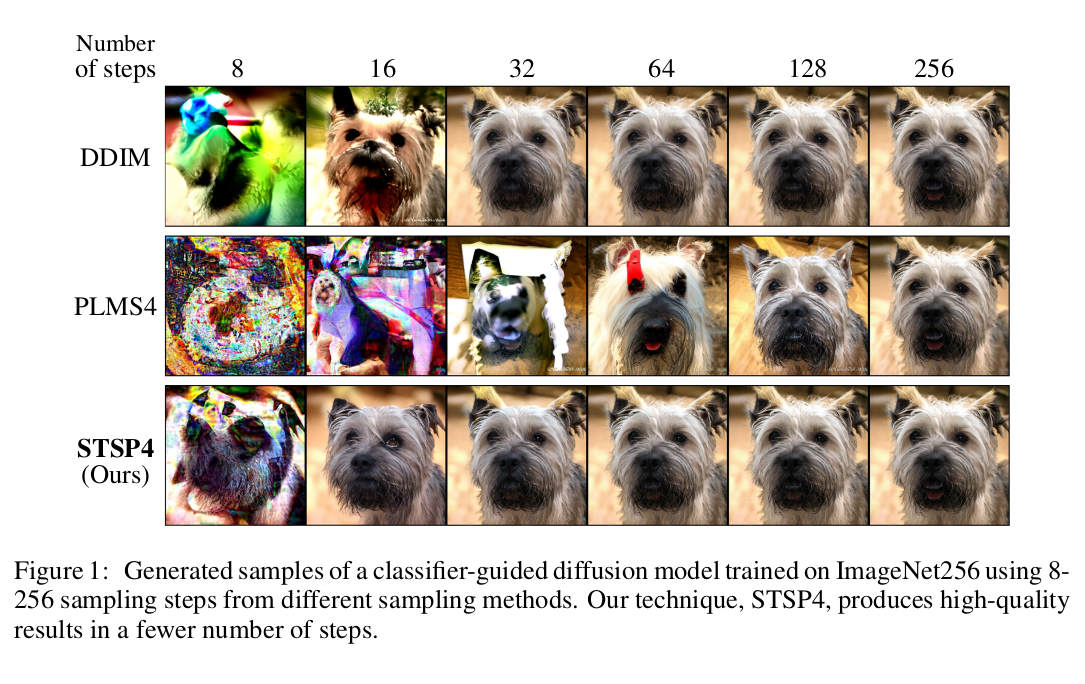
Proposing efficient diffusion models that require less computation is a major challenge, but ultimately the contribution of this article goes beyond this scope. It is part of the literature on neural ODEs and their associated integration schemes. Here, the authors focus specifically on improving a class of generative models, but the scope of this type of approach could be applied to any type of architecture that can be interpreted as a solution to a differential equation.
review the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to join our 14k+ ML SubReddit, discord channeland electronic newsletterwhere we share the latest AI research news, exciting AI projects, and more.
Simon Benaïchouche received his M.Sc. in Mathematics in 2018. He is currently a Ph.D. candidate at IMT Atlantique (France), where his research focuses on the use of deep learning techniques for data assimilation problems. His experience includes inverse problems in geosciences, uncertainty quantification, and learning physical systems from data.





