Supresión de errores cuánticos escalando un qubit lógico de código de superficie – Google AI Blog

Dentro de muchos años, los científicos podrán usar computadoras cuánticas tolerantes a fallas para cálculos a gran escala con aplicaciones en la ciencia y la industria. Estas computadoras cuánticas serán mucho más grandes que las actuales y consistirán en millones de bits cuánticos coherentes o qubits. Pero hay una trampa: estos componentes básicos deben ser lo suficientemente buenos o los sistemas se llenarán de errores.

Actualmente, las tasas de error de los qubits en nuestra tercera generación El procesador Sycamore está típicamente entre 1 en 10,000 a 1 en 100. A través de nuestro trabajo y la de otros, entendemos que desarrollar computadoras cuánticas a gran escala requerirá tasas de error mucho más bajas. Necesitaremos tasas en el rango de 1 en 10⁹ a 1 en 10⁶ para ejecutar circuitos cuánticos que pueden resolver problemas industrialmente relevantes.

Entonces, ¿cómo llegamos allí, sabiendo que es poco probable obtener un mejor rendimiento de tres a seis órdenes de magnitud de nuestros qubits físicos actuales? Nuestro equipo ha creado una hoja de ruta que ha dirigido nuestra investigación durante los últimos años, mejorando el rendimiento de nuestras computadoras cuánticas en pasos graduales hacia una computadora cuántica tolerante a fallas.

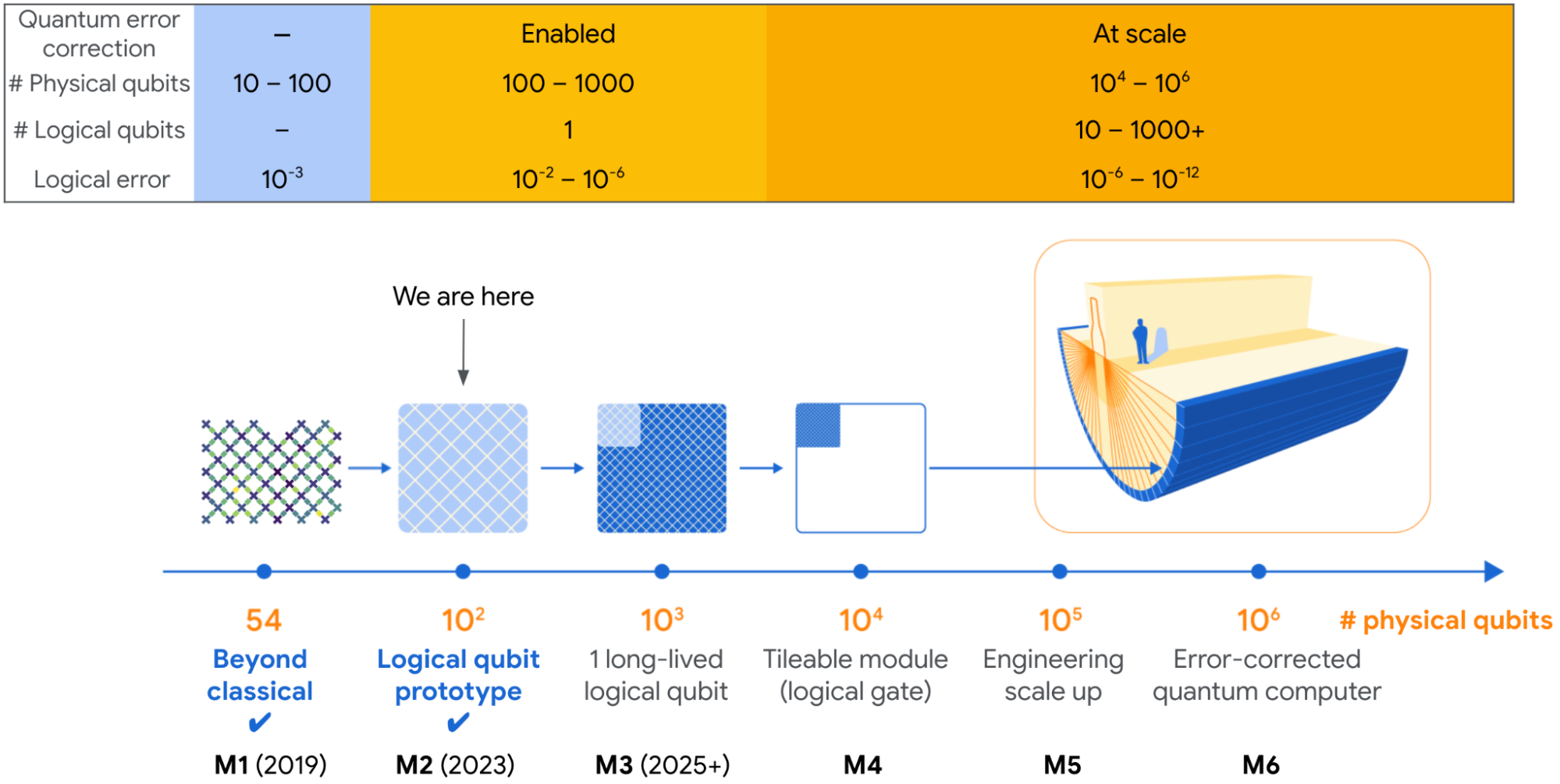Hoja de ruta para construir una computadora cuántica útil con corrección de errores con hitos clave. Actualmente estamos construyendo un qubit lógico que escalaremos en el futuro.

Hoy en “Supresión de errores cuánticos escalando un Qubit lógico de código de superficie“, publicado en Naturaleza, estamos anunciando que hemos alcanzado el segundo hito en nuestra hoja de ruta. Nuestros resultados experimentales demuestran un prototipo de la unidad básica de una computadora cuántica con corrección de errores conocida como qubit lógicocon un rendimiento que se acerca al régimen que permite la computación cuántica tolerante a fallas y escalable.

De qubits físicos a qubits lógicos

La corrección de errores cuánticos (QEC) representa un cambio significativo con respecto a la computación cuántica actual, donde cada qubit físico del procesador actúa como una unidad de computación. Proporciona la receta para alcanzar errores bajos intercambiando muchos bien qubits para un excelente uno: la información se codifica en varios qubits físicos para construir un solo qubit lógico que es más resistente y capaz de ejecutar algoritmos cuánticos a gran escala. En las condiciones adecuadas, cuantos más qubits físicos se utilicen para construir un qubit lógico, mejor será ese qubit lógico.

Sin embargo, esto no funcionará si los errores agregados de cada qubit físico adicional superan los beneficios de QEC. Hasta ahora, las altas tasas de error físico siempre han ganado.

Con ese fin, usamos un código de corrección de errores particular llamado código de superficie y mostrar por primera vez que aumentar el tamaño del código disminuye la tasa de error del qubit lógico. Por primera vez en cualquier plataforma de computación cuántica, esto se logró mitigando minuciosamente muchas fuentes de error a medida que escalamos de 17 a 49 qubits físicos. Este trabajo es evidencia de que, con suficiente cuidado, podemos producir los qubits lógicos necesarios para una computadora cuántica con corrección de errores a gran escala.

Corrección de errores cuánticos con códigos de superficie

¿Cómo protege la información un código de corrección de errores? Tome un ejemplo simple de la comunicación clásica: Bob quiere enviar a Alice un solo bit que dice “1” a través de un canal de comunicación ruidoso. Al reconocer que el mensaje se pierde si el bit cambia a “0”, Bob envía tres bits: “111”. Si uno voltea por error, Alice podría tomar un voto mayoritario (un código simple de corrección de errores) de todos los bits recibidos y aún así entender el mensaje deseado. Repetir la información más de tres veces (aumentar el “tamaño” del código) permitiría que el código tolerara más errores individuales.

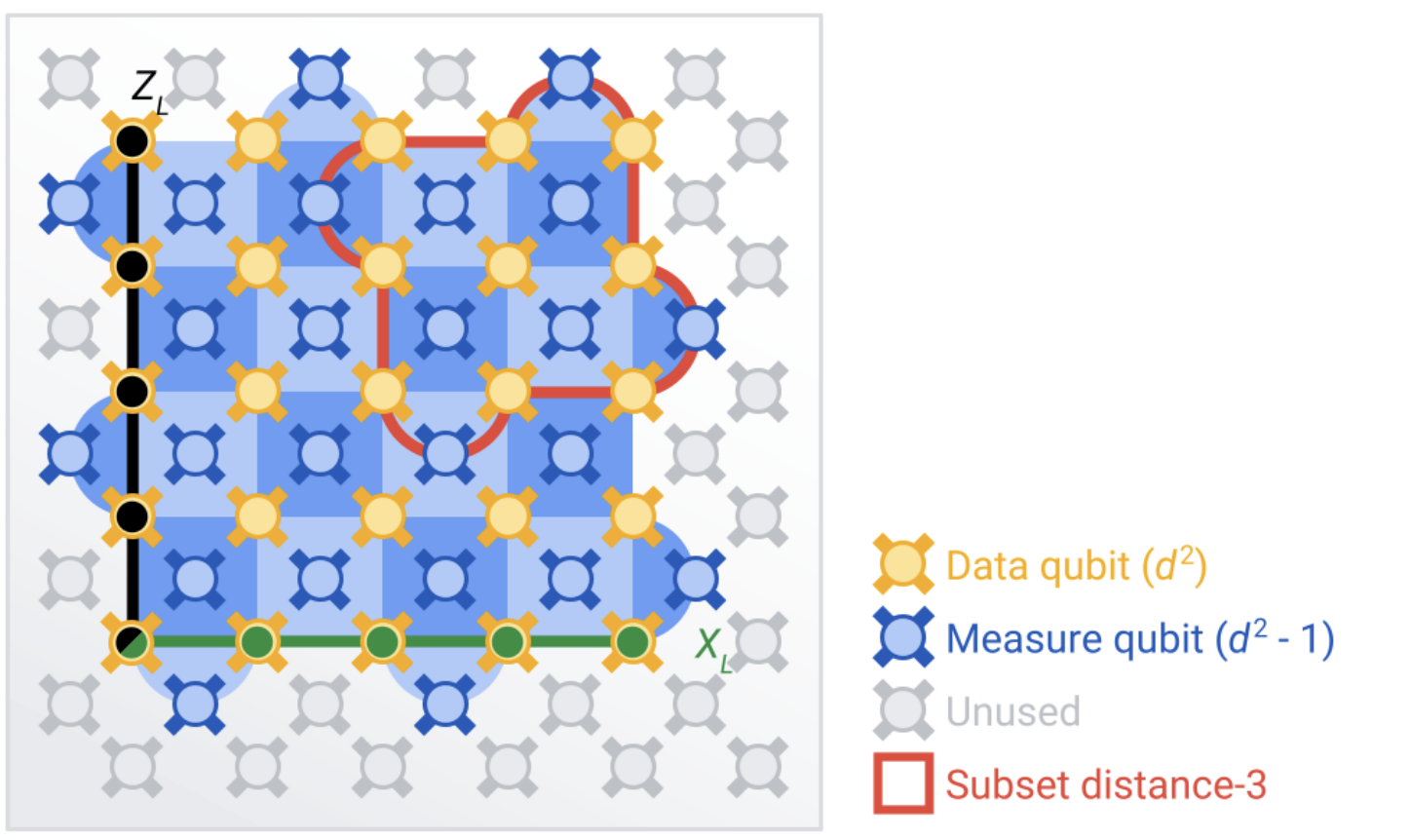Muchos qubits físicos en un procesador cuántico que actúan como un qubit lógico en un código de corrección de errores llamado código de superficie.

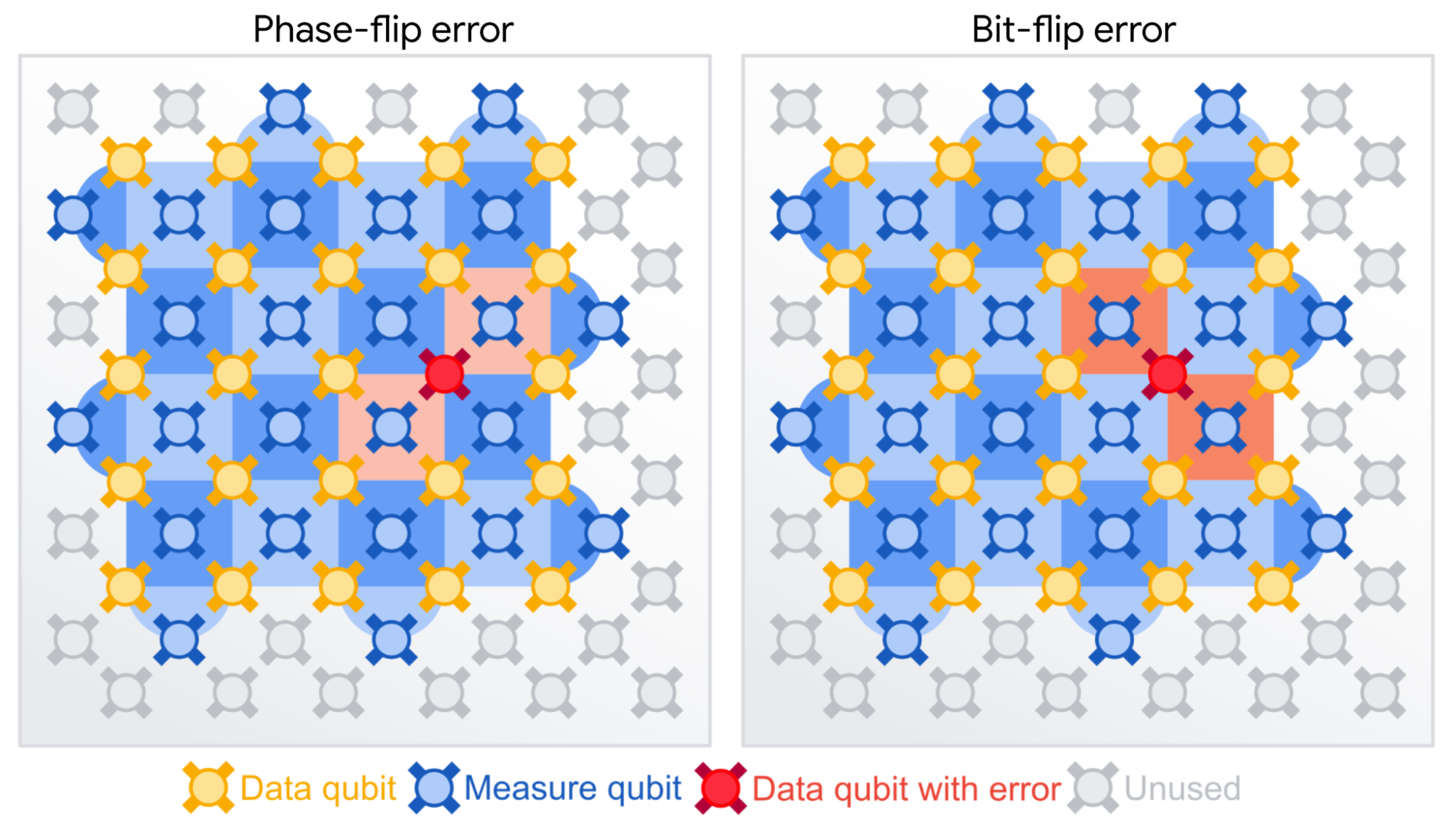
Un código de superficie toma este principio e imagina una implementación cuántica práctica. Tiene que satisfacer dos restricciones adicionales. En primer lugar, el código de superficie debe ser capaz de corregir no solo cambios de bits, sino que también debe tomar un qubit de |0⟩ a |1⟩pero también fase voltea Este error es exclusivo de los estados cuánticos y transforma un qubit en un superposición estado, por ejemplo de “|0⟩ + |1⟩” a “|0⟩ – |1⟩”. En segundo lugar, verificar los estados de los qubits destruiría sus superposiciones, por lo que se necesita una forma de detectar errores sin medir los estados directamente.

Para abordar estas limitaciones, organizamos dos tipos de qubits en un tablero de ajedrez. Los qubits de “datos” en los vértices forman el qubit lógico, mientras que los qubits de “medida” en el centro de cada cuadrado se utilizan para las llamadas “medidas estabilizadoras”. Estas medidas nos dicen si los qubits son todos iguales, como se desea, o diferentes, lo que indica que ocurrió un error, sin revelar realmente el valor de los qubits de datos individuales.

Colocamos en mosaico dos tipos de medidas de estabilizador en un patrón de tablero de ajedrez para proteger los datos lógicos de los cambios de bit y de fase. Si algunas de las mediciones del estabilizador registran un error, entonces se usan las correlaciones en las mediciones del estabilizador para identificar qué error(es) ocurrió(n) y dónde.

QEC de código de superficie. qubits de datos (amarillo) están en los vértices de un tablero de ajedrez. Los qubits de medida en el centro de cada cuadrado se utilizan para las medidas del estabilizador (cuadrados azules). Los cuadrados azul oscuro verifican los errores de cambio de bits, mientras que los cuadrados azul claro verifican los errores de cambio de fase. Izquierda: Un error de cambio de fase. Las dos mediciones del estabilizador azul claro más cercanas registran el error (luz roja). Bien: Un error de cambio de bit. Las dos mediciones de estabilizador azul oscuro más cercanas registran el error (rojo oscuro).

Así como el mensaje de Bob a Alice en el ejemplo anterior se volvió más sólido contra errores con el aumento del tamaño del código, un código de superficie más grande protege mejor la información lógica que contiene. El código de superficie puede soportar una cantidad de errores de cambio de fase y bit, cada uno igual a menos de la mitad del distanciadonde la distancia es el número de qubits de datos que abarcan el código de superficie en cualquier dimensión.

Pero aquí está el problema: cada qubit físico individual es propenso a errores, por lo que cuantos más qubits hay en un código, más posibilidades de errores. Queremos que la mayor protección que ofrece QEC compense las mayores oportunidades de errores a medida que aumentamos la cantidad de qubits. Para que esto suceda, los qubits físicos deben tener errores por debajo del llamado “umbral tolerante a fallas”. Para el código de superficie, este umbral es bastante bajo. Tan bajo que no ha sido experimentalmente factible hasta hace poco. Ahora estamos al borde de alcanzar este codiciado régimen.

Hacer y controlar qubits físicos de alta calidad

Entrar en el régimen en el que QEC mejora con la escala requería mejorar todos los aspectos de nuestras computadoras cuánticas, desde la nanofabricación de los qubits físicos hasta el control optimizado del sistema cuántico completo. Estos experimentos se ejecutaron en una arquitectura de procesador Sycamore de tercera generación de última generación optimizada para QEC utilizando el código de superficie con mejoras en todos los ámbitos:

• Aumento de la relajación de los qubits y desfase de la vida útil a través de un proceso de fabricación mejorado y una reducción del ruido ambiental cerca del procesador cuántico.
• Disminución de la diafonía entre todos los qubits físicos durante el funcionamiento en paralelo mediante la optimización del diseño del circuito del procesador cuántico y la nanofabricación.
• Deriva reducida y fidelidad de control de qubit mejorada a través de electrónica personalizada mejorada.
• Se implementaron operaciones de reinicio y lectura más rápidas y de mayor fidelidad en comparación con las generaciones anteriores del procesador Sycamore.
• Reducción de los errores de calibración mediante el modelado extensivo del sistema cuántico completo y el empleo de mejores algoritmos de optimización del sistema.
• Desarrolló calibraciones conscientes del contexto y totalmente paralelas para minimizar la deriva y optimizar los parámetros de control para los circuitos QEC.
• Protocolos de desacoplamiento dinámico mejorados para proteger los qubits físicos del ruido y la diafonía durante las operaciones de inactividad.

Correr circuitos de código de superficie

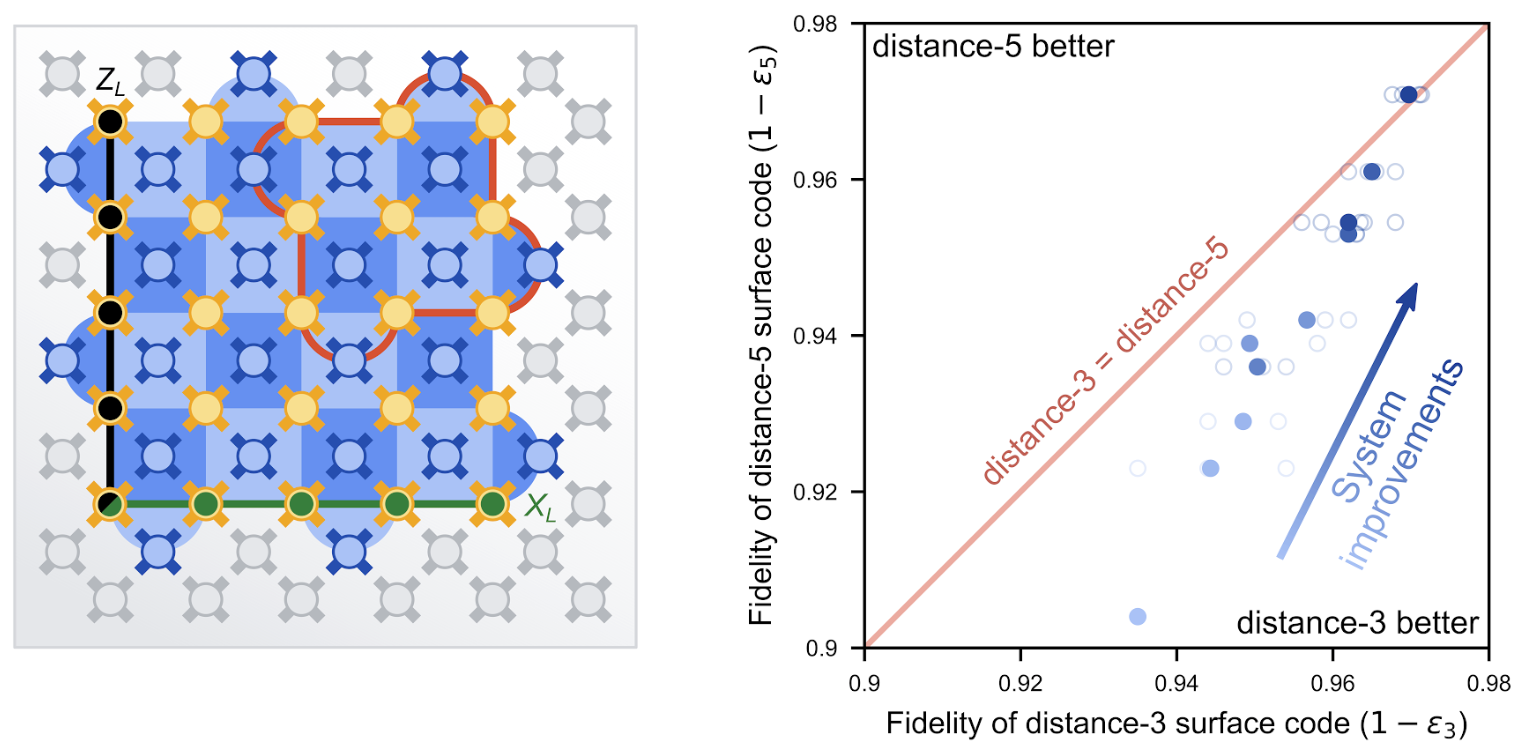
Con estas actualizaciones implementadas, realizamos experimentos para comparar la proporción (𝚲_3,5) entre la tasa de error lógico de un código de superficie de distancia 3 (ε₃) con 17 qubits al de un código de superficie de distancia-5 (ε₅) con 49 qubits — 𝚲_3,5 = mi₃ / mi₅.

Comparación de la fidelidad lógica (definida como 1-ε) entre códigos de superficie de distancia-3 (d=3) y distancia-5 (d=5). El código de distancia 5 contiene cuatro arreglos posibles de distancia 3, con un ejemplo que se muestra en el contorno rojo (izquierda). A medida que se realizaron mejoras, la fidelidad de d=5 aumentó más rápido que la de d=3, superando finalmente el código de distancia 3, como se muestra en los puntos de datos de la parte superior derecha (bien), cuyo promedio se encuentra ligeramente a la izquierda de la ε3 = mi5 línea.

Los resultados de estos experimentos se muestran arriba a la derecha. Las mejoras continuas durante varios meses nos permitieron reducir los errores lógicos de ambas cuadrículas, lo que llevó a la cuadrícula de distancia 5 (ε₅ = 2,914 %) superando a las cuadrículas de distancia 3 (ε₃ = 3,028%) en un 4% (𝚲_3,5 = 1.04) con 5𝛔 de confianza. Si bien esto puede parecer una pequeña mejora, es importante enfatizar que el resultado representa una novedad en el campo desde 1995 de Peter Shor. propuesta QEC. Un código más grande que supera a uno más pequeño es una firma clave de QEC, y todas las arquitecturas de computación cuántica deberán superar este obstáculo para lograr un camino hacia los errores bajos que son necesarios para las aplicaciones cuánticas.

el camino a seguir

Estos resultados indican que estamos entrando en una nueva era de QEC práctico. El equipo de Google Quantum AI ha pasado los últimos años pensando en cómo definimos el éxito en esta nueva era y cómo medimos el progreso en el camino.

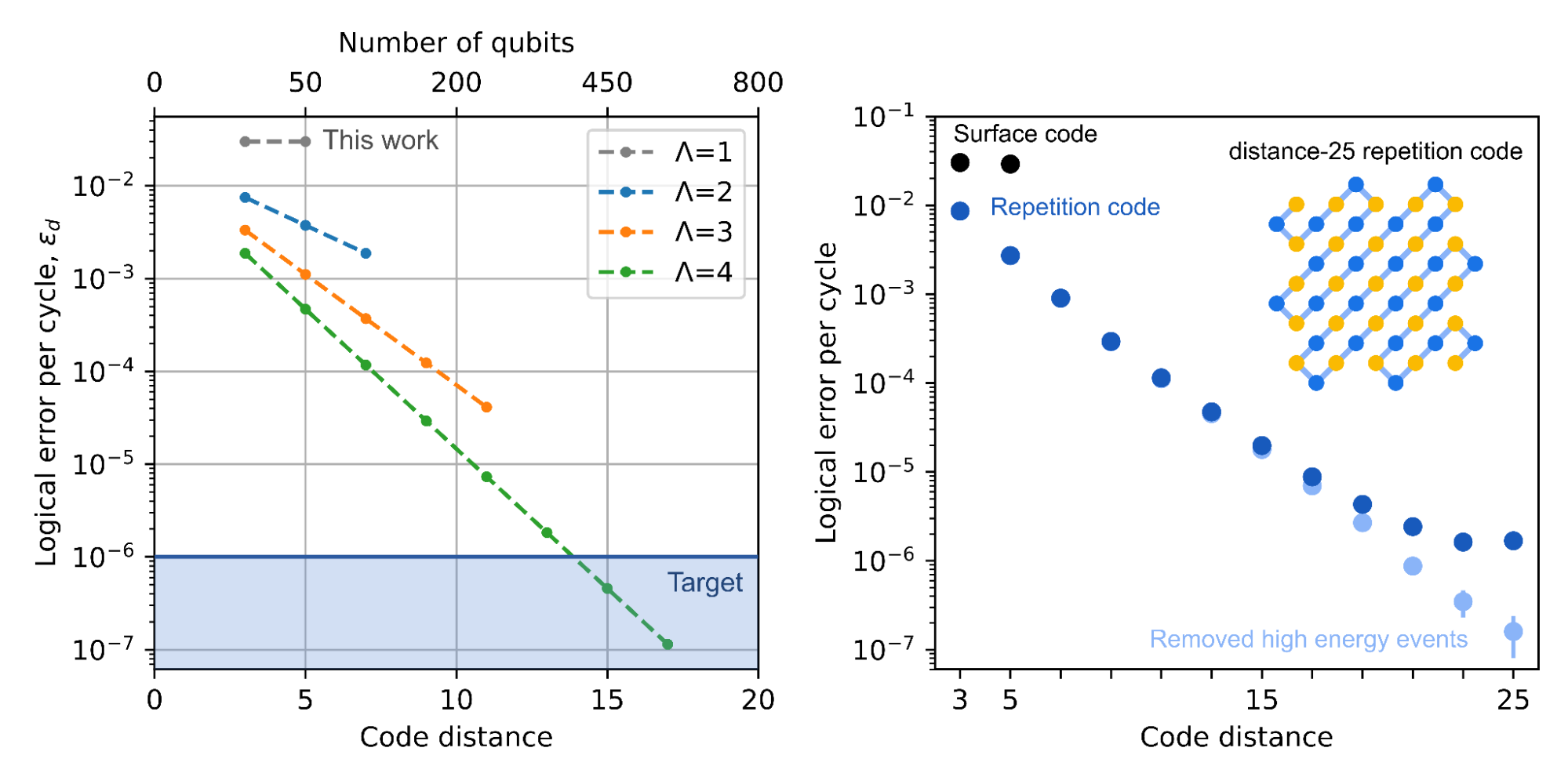
El objetivo final es demostrar un camino para lograr los errores bajos necesarios para usar computadoras cuánticas en aplicaciones significativas. Para ello, nuestro objetivo sigue siendo lograr tasas de error lógico de 1 en 10⁶ o menor por ciclo de QEC. En la figura de abajo a la izquierda, delineamos el camino que anticipamos para alcanzar este objetivo. A medida que continuamos mejorando nuestros qubits físicos (y, por lo tanto, el rendimiento de nuestros qubits lógicos), esperamos aumentar gradualmente 𝚲 de cerca de 1 en este trabajo a números más grandes. La siguiente figura muestra que un valor de 𝚲 = 4 y una distancia de código de 17 (577 qubits físicos con una calidad suficientemente buena) generará una tasa de error lógico por debajo de nuestro objetivo de 1 en 10⁶.

Aunque todavía faltan algunos años para este resultado, tenemos una técnica experimental para probar tasas de error tan bajas con el hardware actual, aunque en circunstancias limitadas. Si bien los códigos de superficie bidimensionales nos permiten corregir errores de cambio de fase y de bits, también podemos construir códigos de repetición unidimensionales que solo pueden resolver un tipo de error con requisitos relajados. Abajo a la derecha, mostramos que un código de repetición de distancia 25 puede alcanzar tasas de error por ciclo cercanas a 1 en 10⁶. Con errores tan bajos, vemos nuevos tipos de mecanismos de error que aún no son observables con nuestros códigos de superficie. Al controlar estos mecanismos de error, podemos mejorar los códigos de repetición a tasas de error cercanas a 1 en 10⁷.

Izquierda: progresión esperada a medida que mejoramos el rendimiento (cuantificado por 𝚲) y la escala (cuantificada por la distancia del código) para los códigos de superficie. Bien: Índices de error lógico medidos experimentalmente por ciclo frente a la distancia de códigos de repetición unidimensionales y códigos de superficie bidimensionales.

Alcanzar este hito refleja tres años de trabajo concentrado por parte de todo el equipo de Google Quantum AI luego de nuestra demostración de una computadora cuántica que supera a una computadora clásica. En nuestra marcha hacia la construcción de computadoras cuánticas tolerantes a fallas, continuaremos usando las tasas de error objetivo en la figura anterior para medir nuestro progreso. Con mejoras adicionales hacia nuestro próximo hito, anticipamos ingresar al régimen tolerante a fallas, donde podemos suprimir exponencialmente los errores lógicos y desbloquear las primeras aplicaciones cuánticas útiles con corrección de errores. Mientras tanto, seguimos explorando varias formas de resolver problemas utilizando computadoras cuánticas en temas que van desde la física de la materia condensada hasta la química, el aprendizaje automático y la ciencia de los materiales.