Recently, ai Agents have shown very promising developments in automating the proving of mathematical theorems and verifying the correctness of code using tools such as Lean. These tools combine code with specifications and tests to ensure that it meets intended requirements, providing very strong safeguards in safety-critical applications. artificial intelligence has shown that it can enable the fundamental steps of solution development, that is, coding, specifying and testing, through large language models. While these advances hold great promise, fully automating program verification remains a challenge.
Traditionally, the proof of mathematical theorems has been based on tools such as Leanwhich trains models on data sets like Matelib Solve problems using specific definitions and strategies. However, these tools have had difficulty adapting to program verification, which requires completely different methods and approaches. While machine learning has improved automation in systems like Coq and Isabelle, similar advances are still missing for Lean in program verification. Other tools like dafny and TRUEas well as landmarks such as miniF2F and CoqGymoffer alternatives. Still, they have not been able to fully address the challenges of adapting mathematical theorem proving methods to the needs of program verification.
To solve this, researchers from Carnegie Mellon University proposed miniCodePropsa reference point that contains 201 program specifications Lean Test Wizard, to address the challenge of automatically generating tests for programs and their specifications. miniCodeProps It contained simple, stand-alone programs like lists, natural numbers, and binary treeswith different levels of difficulty to demonstrate. The data set, divided into three categories:intuitive properties of lists, trees and numbers (medley), termination lemmas for recursive functions (termination), and properties of non-standard classification algorithms (classification)—including 201 statements of theorems. The functions operated primarily on linked lists, and some involved natural numbers and binary trees. These properties were classified by difficulty: easy (mix), medium (completion), and difficult (sort). The termination lemmas required proving the termination of recursion, which was critical for the use of Lean 4. The data set, available in jsonlines format, included essential details such as the proof status and dependencies of each theorem. Examples such as the zip concatenation property and sorting properties highlighted the challenge of testing these properties, especially for more complex sorting algorithms.
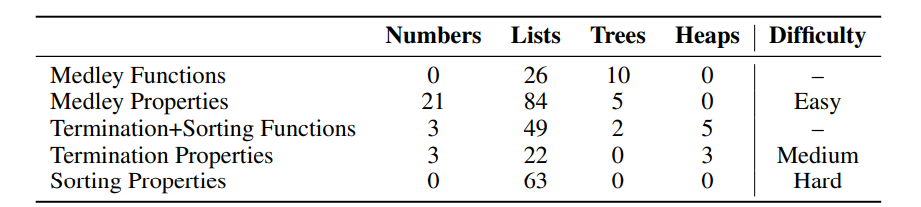
The evaluation of miniCodeProps focused on two main tasks: full generation and tactic-by-tactic generation. In full test generation, the models were tested for their ability to generate full tests for given specifications. For tactic-by-tactic generation, models were evaluated based on their ability to suggest the next appropriate tactic from the current test state, testing incremental reasoning. The evaluation also considered test difficulty levels, ranging from simple properties of lists and numbers to complex properties of sorting and completion algorithms, measuring both efficiency and correctness in test generation or tactical application.
The results indicated that neural theorem provers, such as GPT-4o, performed well on simpler tasks, achieving a 75.6% success rate on combined properties. However, performance on more difficult tasks, such as completion and sorting, was lower, in 4.34% and 6.96%respectively. The model trained by Mathlib ntp-ctx-1.3B demonstrated similar efficiency to GPT-4o, suggesting the potential for domain-specific checkers to show more promise. MiniCodeProps provides a framework to enhance automated theorem proving agents for code verification, supporting human engineers, and offering additional guarantees through various reasoning approaches.
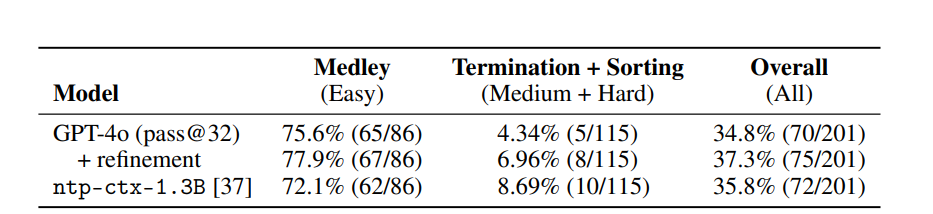
In the end, the proposed miniCodeProps is a valuable benchmark that can be used to advance automation. PTI-based code verification. It contains problems from a variety of inductive problem data sets, allowing step-by-step progress in verifying program properties. However, the method showed limitations and cannot effectively solve complicated problems. Minicode Accessories It can potentially drive advances in verification agents and serve as a basis for evaluating new approaches in automated code verification.
Verify he Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on <a target="_blank" href="https://twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. Don't forget to join our SubReddit over 60,000 ml.
Trending: LG ai Research launches EXAONE 3.5 – three frontier-level bilingual open-source ai models that deliver unmatched instruction following and broad context understanding for global leadership in generative ai excellence….
Divyesh is a Consulting Intern at Marktechpost. He is pursuing a BTech in Agricultural and Food Engineering from the Indian Institute of technology Kharagpur. He is a data science and machine learning enthusiast who wants to integrate these leading technologies in agriculture and solve challenges.
<script async src="//platform.twitter.com/widgets.js” charset=”utf-8″>






