Eleuther AI introduces new machine learning framework to analyze neural network training via Jacobian matrix

Neural networks have become fundamental tools in computer vision, NLP, and many other fields, offering capabilities to model and predict complex patterns. The training process is at the core of neural network functionality, where network parameters are iteratively adjusted to minimize error using optimization techniques such as gradient descent. This optimization occurs in a high-dimensional parameter space, making it difficult to decipher how the initial parameter settings influence the final trained state.

Although progress has been made in the study of these dynamics, doubts still remain about the dependence of the final parameters on their initial values ​​and the role of input data remain to be answered. Researchers seek to determine whether specific initializations lead to unique optimization paths or whether transformations are predominantly governed by other factors such as architecture and data distribution. This understanding is essential to design more efficient training algorithms and improve the interpretability and robustness of neural networks.

Previous studies have offered insights into the low-dimensional nature of neural network training. Research shows that parameter updates often occupy a relatively small subspace of the overall parameter space. For example, projections of gradient updates onto randomly oriented low-dimensional subspaces tend to have minimal effects on the final network performance. Other studies have observed that most parameters remain close to their initial values ​​during training and updates are typically approximately low range over short intervals. However, these approaches fail to fully explain the relationship between initialization and final states or how specific data structures influence these dynamics.

EleutherAI researchers introduced a novel framework for analyzing neural network training via Jacobian matrix to address the above issues. This method examines the Jacobian of the trained parameters with respect to their initial values, capturing how initialization shapes the final states of the parameters. By applying singular value decomposition to this matrix, the researchers decomposed the training process into three distinct subspaces:

1. chaotic subspace
2. Bulk subspace
3. stable subspace

This decomposition provides a detailed understanding of the influence of initialization and data structure on training dynamics, offering a new perspective on the optimization of neural networks.

The methodology involves linearizing the training process around the initial parameters, allowing the Jacobian matrix to map how small initialization perturbations propagate during training. Singular value decomposition revealed three distinct regions in the Jacobian spectrum. The chaotic region, comprising approximately 500 singular values ​​significantly larger than one, represents directions where parameter changes are amplified during training. The massive region, with around 3000 singular values ​​close to one, corresponds to dimensions where the parameters remain virtually unchanged. The stable region, with approximately 750 singular values ​​less than one, indicates directions where changes are damped. This structured decomposition highlights the varying influence of parameter space directions on training progress.

In experiments, the chaotic subspace shapes the optimization dynamics and amplifies parameter perturbations. Stable subspace ensures smoother toe-in by dampening shifts. Interestingly, despite occupying 62% of the parameter space, the massive subspace has minimal influence on behavior within the distribution, but significantly affects predictions for data outside the distribution. For example, perturbations along bulk directions leave test set predictions largely unchanged, while those in chaotic or stable subspaces can alter the results. Restricting training to the bulk subspace made gradient descent ineffective, while training on chaotic or stable subspaces achieved comparable performance to unconstrained training. These patterns were consistent across different initializations, loss functions, and data sets, demonstrating the robustness of the proposed framework. Experiments with a multilayer perceptron (MLP) with a hidden layer of width 64, trained on the UCI Digits dataset, confirmed these observations.

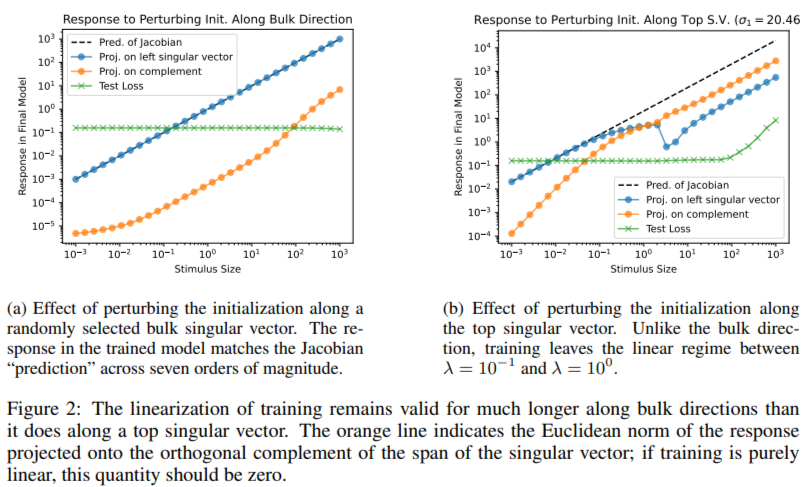
Several conclusions emerge from this study:

• The chaotic subspace, comprising approximately 500 singular values, amplifies parameter perturbations and is instrumental in shaping the optimization dynamics.
• With around 750 singular values, the stable subspace effectively buffers perturbations, contributing to smooth and stable training convergence.
• The massive subspace, which represents 62% of the parameter space (approximately 3000 singular values), remains virtually unchanged during training. It has minimal impact on behavior within the distribution, but significant effects on predictions outside the distribution.
• Perturbations along chaotic or stable subspaces alter the network outputs, while massive perturbations leave test predictions largely unaffected.
• Restricting training to bulk subspace makes optimization ineffective, while training limited to chaotic or stable subspaces has performance comparable to full training.
• The experiments consistently demonstrated these patterns on different data sets and initializations, highlighting the generality of the findings.

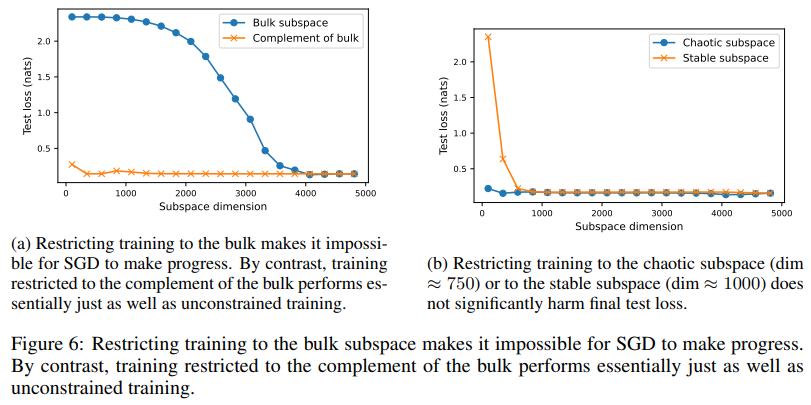
In conclusion, this study presents a framework for understanding the dynamics of neural network training by decomposing parameter updates into chaotic, stable, and massive subspaces. It highlights the intricate interplay between initialization, data structure, and parameter evolution, providing valuable insights into how training proceeds. The results reveal that the chaotic subspace drives optimization, the stable subspace ensures convergence, and the massive subspace, although large, has minimal impact on the distribution behavior. This nuanced understanding challenges conventional assumptions about uniform parameter updates. Provides practical ways to optimize neural networks.

Verify he Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on <a target="_blank" href="https://twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. Don't forget to join our SubReddit over 60,000 ml.

Trending: LG ai Research launches EXAONE 3.5 – three frontier-level bilingual open-source ai models that deliver unmatched instruction following and broad context understanding for global leadership in generative ai excellence….

Asif Razzaq is the CEO of Marktechpost Media Inc.. As a visionary entrepreneur and engineer, Asif is committed to harnessing the potential of artificial intelligence for social good. Their most recent endeavor is the launch of an ai media platform, Marktechpost, which stands out for its in-depth coverage of machine learning and deep learning news that is technically sound and easily understandable to a wide audience. The platform has more than 2 million monthly visits, which illustrates its popularity among the public.