Matrix-Free Differentiation: Advances in Probabilistic Machine Learning

Automatic differentiation has transformed machine learning model development by eliminating complex, application-dependent gradient derivations. This transformation helps to calculate vector-jacobian and vector-Jacobian products without creating the full Jacobian matrix, which is crucial for tuning scientific and probabilistic machine learning models. Otherwise, a column would be needed for each parameter of the neural network. Today, anyone can build algorithms around large matrices by taking advantage of this matrix-free approach. However, differentiable linear algebra for Jacobian vector products and similar operations has remained largely unexplored to this day and traditional methods also have some defects.

Current methods for evaluating functions of large matrices are mainly based on Lanczos and Arnoldi iterations, which require good computing power and are not optimized for differentiation. The generative models mainly depended on the variable change formula, which involves the logarithmic determinant of the Jacobian matrix of a neural network. To optimize model parameters in Gaussian processes, it is important to compute gradients of log likelihood functions involving many large covariance matrices. Use methods that combine the estimation of random traces with the Lanczos Iteration helps increase the speed of convergence. Some of the recent work uses some combination of stochastic trace estimation with the Lanczos iteration and agrees on gradients of logarithmic determinants. Unlike Gaussian processes, previous work on Laplace approximations attempts to simplify the Generalized Gauss-Newton (GGN) matrix using only certain groups of network weights or using various algebraic techniques such as diagonal or low-rank approximations. These methods facilitate the automatic calculation of logarithmic determinants, but lose important details about the correlation between weights.

To mitigate these challenges and as a step toward exploring differentiable linear algebra, the researchers proposed a new matrix-free method to automatically differentiate matrix functions.

A group of researchers from Technical University of Denmark and Kongens Lyngby, Denmarkconducted detailed research and derived previously unknown attachment systems for Lanczos and arnold iterations, implementing them in JAXand showed that the resulting code could compete with diffraction when it comes to differentiating PDEs, GPyTorch to select Gaussian process models. Additionally, it outperforms standard factorization methods for calibrating Bayesian neural networks.

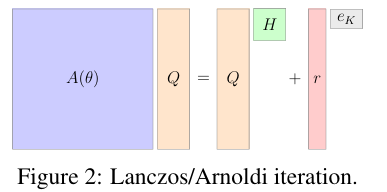
In this, the researchers mainly focused on matrix-free algorithms that avoid direct matrix storage and instead operate via matrix vector products. He Lanczos and arnold Iterations are popular for matrix-free matrix decomposition, producing smaller, structured matrices that approximate the large matrix, making it easier to evaluate matrix functions. The proposed method can efficiently find the derivatives of functions related to large matrices without creating the entire Jacobian matrix. This matrix-free approach evaluates products of Jacobian vectors and Jacobian vectors, making it suitable for large-scale machine learning models. Likewise, the implementation in JAX guarantees high performance and scalability.

The method is similar to the attached method and this new algorithm is faster than back propagation and shares the same stability benefits as the original calculations. The code was tested on three complex machine learning problems to see how it compares to current methods for Gaussian processes, differential equation solvers and Bayesian neural networks. The findings by the researchers show that the integration of Lanczos iterations and Arnoldi methods greatly improves the efficiency and accuracy of machine learning, unlocking new training, testing and calibration techniques and highlighting the importance of advanced mathematical techniques to make machine learning models work better. in different areas.

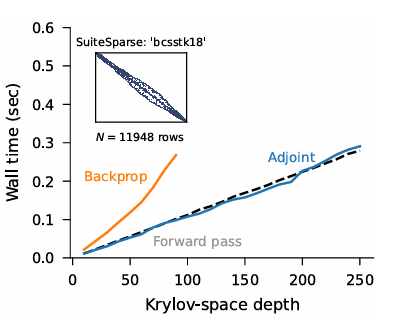
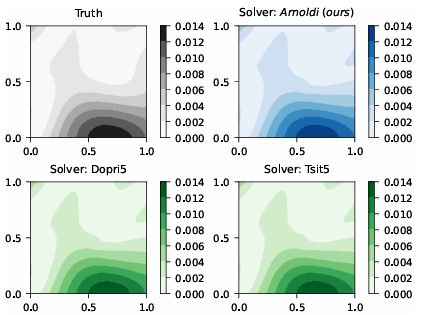
In conclusion, the proposed method mitigates the problems faced by the traditional method and does not require creating large matrices to find the differences in functions. Furthermore, it addresses and resolves the computational difficulties of existing methods and improves the efficiency and accuracy of probabilistic machine learning models. Still, there are certain limitations to this method, such as challenges with direct mode differentiation and the assumption that the orthogonalized array can fit in memory. Future work can extend this framework by addressing these limitations and exploring applications in various fields, especially in machine learning, which may require adaptations for complex value matrices.

look at the Paper. All credit for this research goes to the researchers of this project. Also, don't forget to follow us on twitter.com/Marktechpost”>twitter and join our Telegram channel and LinkedIn Grabove. If you like our work, you will love our information sheet.. Don't forget to join our SubReddit over 55,000ml.

(Sponsorship opportunity with us) Promote your research/product/webinar to over 1 million monthly readers and over 500,000 community members

Divyesh is a Consulting Intern at Marktechpost. He is pursuing a BTech in Agricultural and Food Engineering from the Indian Institute of technology Kharagpur. He is a data science and machine learning enthusiast who wants to integrate these leading technologies in agriculture and solve challenges.