
Author's image
Outliers are abnormal observations that differ significantly from the rest of the data. They can occur due to experimentation error, measurement error, or simply because there is variability within the data itself. These outliers can severely impact the performance of your model, leading to skewed results, similar to how a student with an overachieving relative grade at universities can boost the GPA and affect grading criteria. Handling outliers is a crucial part of the data cleaning procedure.
In this article, I will share how you can detect outliers and different ways to deal with them in your dataset.
Outlier Detection
There are several methods used to detect outliers. If you were to categorize them, here is what they would look like:
- Visualization-based methods: Draw scatter plots or box plots to see the distribution of data and inspect it for outliers.
- Statistical-based methods: These approaches involve z and IQR (interquartile range) scores that offer reliability but may be less intuitive.
I won't cover these methods in depth to keep the topic focused. However, I will include some references at the end for you to explore. In our example, we will use the IQR method. Here's how this method works:
IQR (interquartile range) = Q3 (75th percentile) – Q1 (25th percentile)
The IQR method states that any data point below Q1 – 1.5 * IQR or above Q3 + 1.5 * RIQ are marked as outliers. Let us generate some random data points and detect the outliers using this method.
Perform the necessary imports and generate the random data using np.random:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate random data
np.random.seed(42)
data = pd.DataFrame({
'value': np.random.normal(0, 1, 1000)
})Detect outliers in the dataset using the IQR method:
# Function to detect outliers using IQR
def detect_outliers_iqr(data):
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
return (data < lower_bound) | (data > upper_bound)
# Detect outliers
outliers = detect_outliers_iqr(data('value'))
print(f"Number of outliers detected: {sum(outliers)}")Exit ⇒ Number of outliers detected: 8
Visualize the data set using scatter plots and box plots to see what it looks like.
# Visualize the data with outliers using scatter plot and box plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(range(len(data)), data('value'), c=('blue' if not x else 'red' for x in outliers))
ax1.set_title('Dataset with Outliers Highlighted (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Value')
# Box plot
sns.boxplot(x=data('value'), ax=ax2)
ax2.set_title('Dataset with Outliers (Box Plot)')
ax2.set_xlabel('Value')
plt.tight_layout()
plt.show()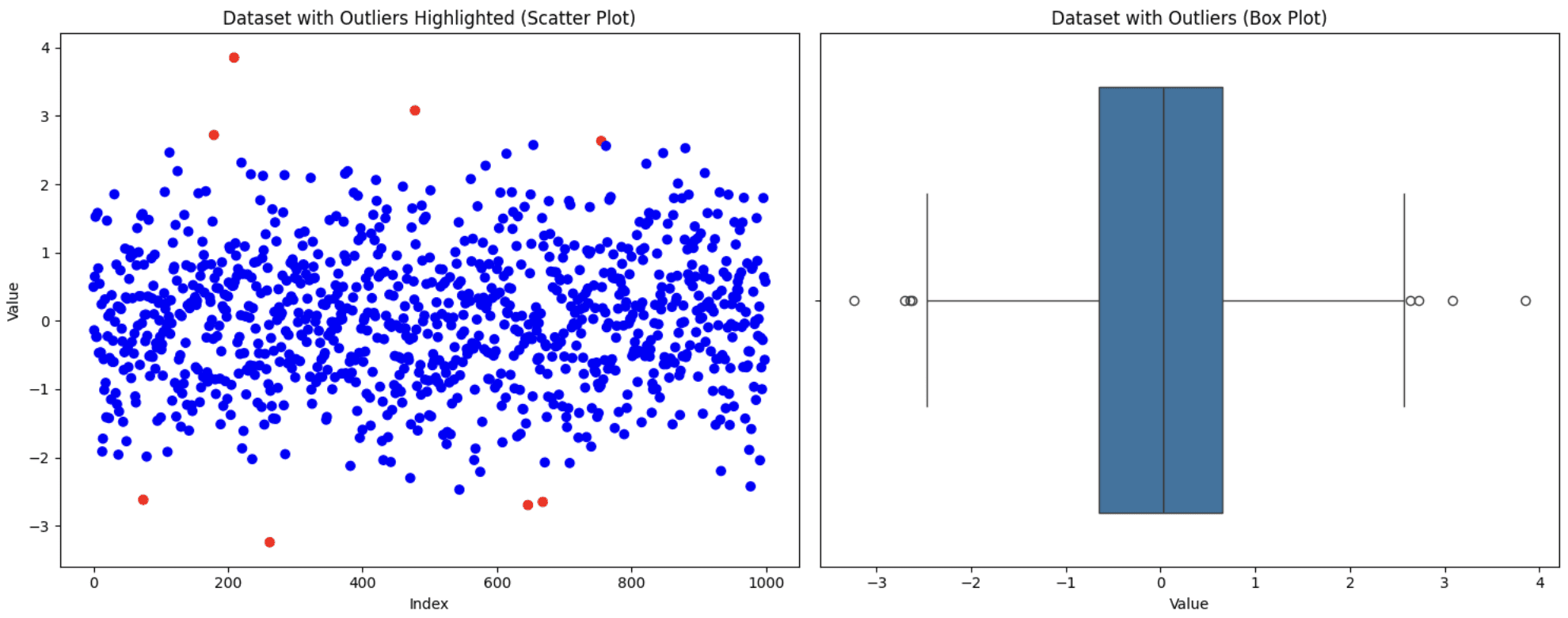

Original dataset
Now that we've spotted outliers, let's look at some of the different ways to handle them.
Handling outliers
1. Removing outliers
This is one of the simplest approaches, but it is not always the right one. You need to take into account certain factors. If removing these outliers significantly reduces the size of your dataset or if they contain valuable information, then excluding them from the analysis will not be the most favorable decision. However, if they are due to measurement errors and are few in number, this approach is suitable. Let's apply this technique to the dataset generated above:
# Remove outliers
data_cleaned = data(~outliers)
print(f"Original dataset size: {len(data)}")
print(f"Cleaned dataset size: {len(data_cleaned)}")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(range(len(data_cleaned)), data_cleaned('value'))
ax1.set_title('Dataset After Removing Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Value')
# Box plot
sns.boxplot(x=data_cleaned('value'), ax=ax2)
ax2.set_title('Dataset After Removing Outliers (Box Plot)')
ax2.set_xlabel('Value')
plt.tight_layout()
plt.show()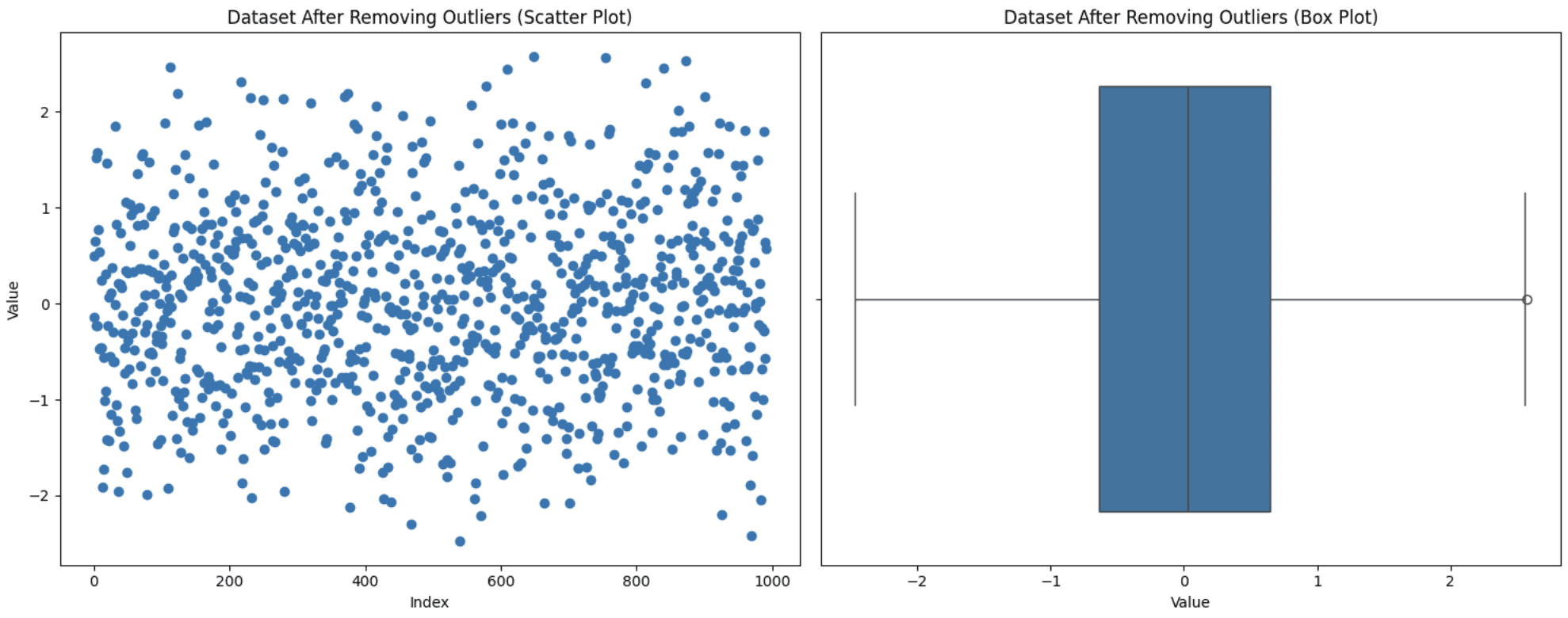

Removing outliers
Note that the distribution of the data can be changed by removing outliers. If you remove some initial outliers, the definition of what an outlier is may change. Therefore, data that would have previously been within the normal range may be considered outliers with a new distribution. You can see a new outlier with the new box plot.
2. Limiting outliers
This technique is used when you do not want to discard data points, but keeping those extreme values can also affect the analysis. So, you set a threshold for the maximum and minimum values and then place the outliers within this range. You can apply this limitation to the outliers or also to the entire dataset. Let’s apply the limitation strategy to our entire dataset to place it within the 5th to 95th percentile range. Here’s how you can execute it:
def cap_outliers(data, lower_percentile=5, upper_percentile=95):
lower_limit = np.percentile(data, lower_percentile)
upper_limit = np.percentile(data, upper_percentile)
return np.clip(data, lower_limit, upper_limit)
data('value_capped') = cap_outliers(data('value'))
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(range(len(data)), data('value_capped'))
ax1.set_title('Dataset After Capping Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Value')
# Box plot
sns.boxplot(x=data('value_capped'), ax=ax2)
ax2.set_title('Dataset After Capping Outliers (Box Plot)')
ax2.set_xlabel('Value')
plt.tight_layout()
plt.show()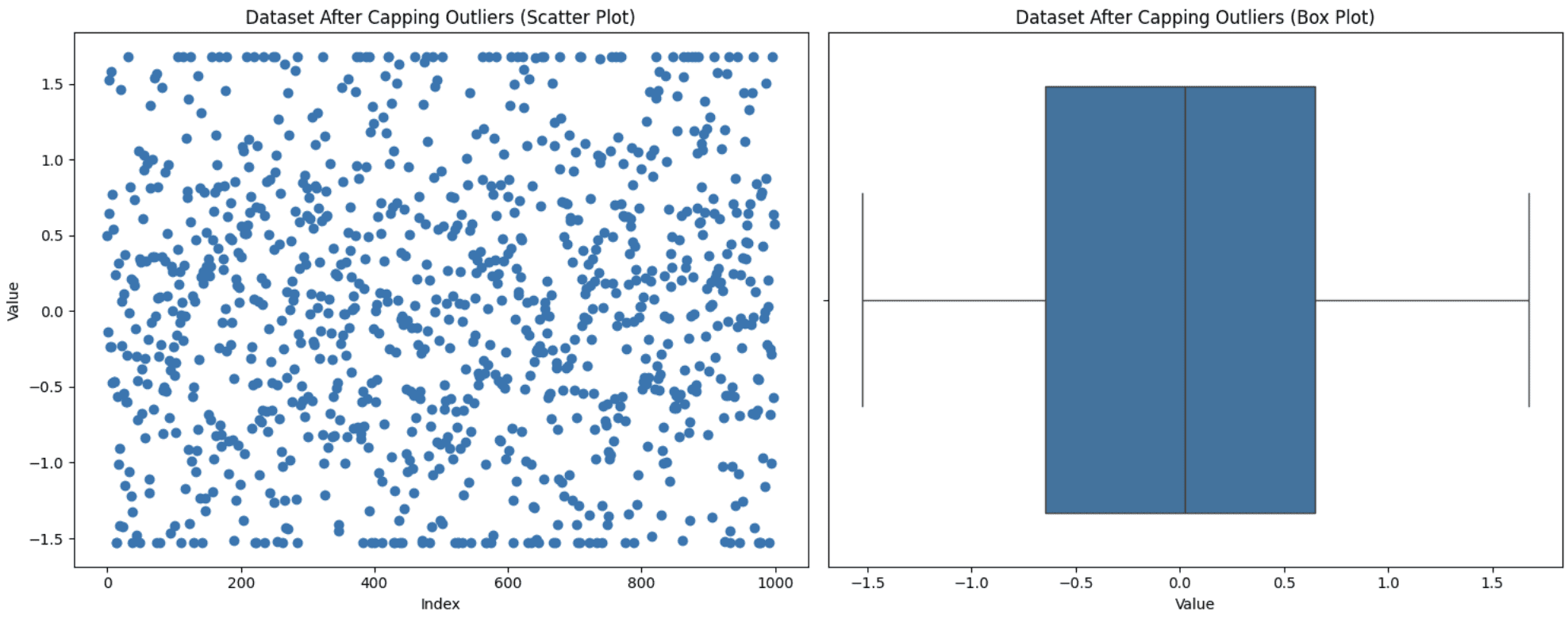

Limiting outliers
It can be seen from the graph that the top and bottom points of the scatter plot appear to be on a line due to the limitation.
3. Imputation of outliers
Sometimes removing values from the analysis is not an option as it may result in loss of information and you also don't want those values to be set to maximum or minimum as in limiting. In this situation, another approach is to replace these values with more meaningful options such as mean, median, or mode. The choice varies depending on the domain of data under observation, but be careful not to introduce bias when using this technique. Let's replace our outliers with the mode value (the value that appears most often) and see how the graph turns out:
data('value_imputed') = data('value').copy()
median_value = data('value').median()
data.loc(outliers, 'value_imputed') = median_value
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(range(len(data)), data('value_imputed'))
ax1.set_title('Dataset After Imputing Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Value')
# Box plot
sns.boxplot(x=data('value_imputed'), ax=ax2)
ax2.set_title('Dataset After Imputing Outliers (Box Plot)')
ax2.set_xlabel('Value')
plt.tight_layout()
plt.show()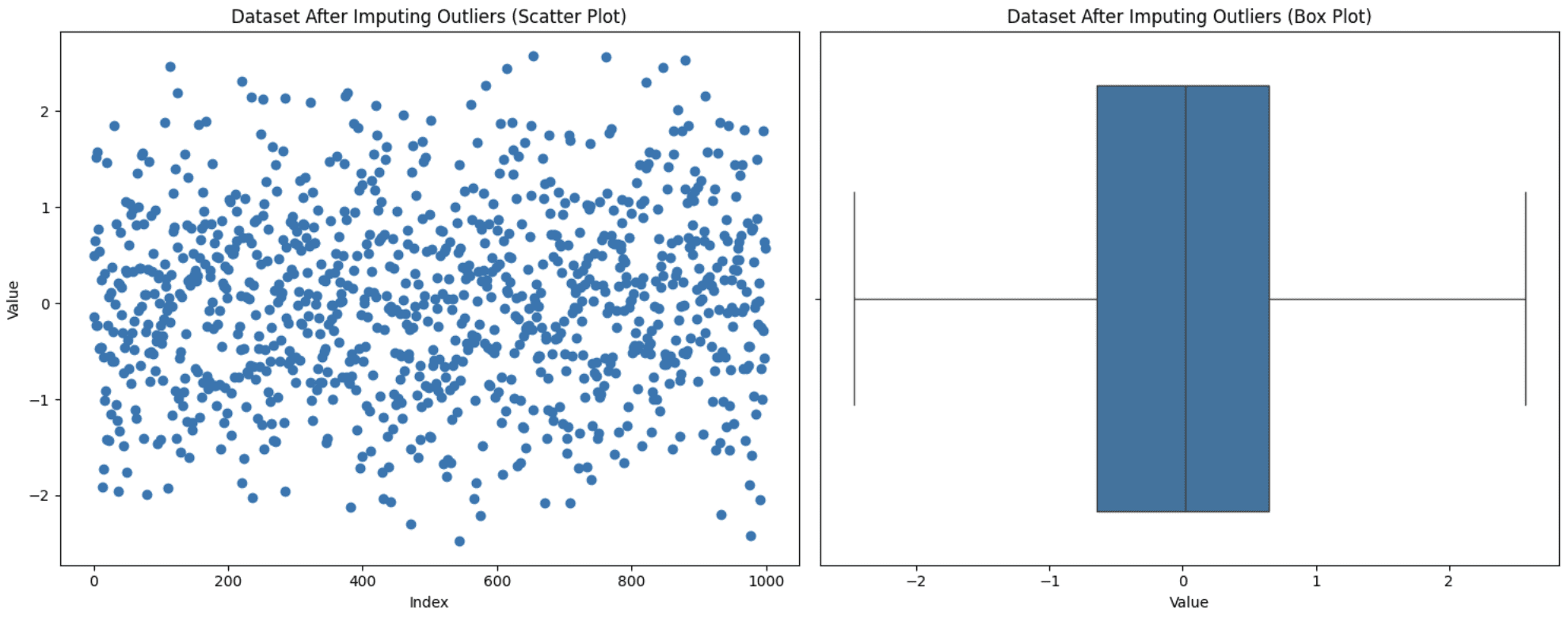

Imputation of outliers
Note that we do not have any outliers now, but this does not guarantee that outliers will be removed, since after imputation the IQR changes as well. You should experiment to see what fits best for your case.
4. Applying a transformation
Transformation is applied to the entire dataset rather than to specific outliers. Basically, the way the data is represented is changed to reduce the impact of outliers. There are various transformation techniques such as logarithmic transformation, square root transformation, Box-Cox transformation, Z-scaling, Yeo-Johnson transformation, min-max scaling, etc. Choosing the right transformation for your case depends on the nature of the data and the ultimate goal of the analysis. Here are some tips to help you select the right transformation technique:
- For right-skewed data: Use the logarithmic, square root, or Box-Cox transformation. The logarithmic transformation is even better when you want to compress small numerical values that are spread over a large scale. The square root transformation is better when, in addition to right skew, you want a less extreme transformation and you also want to handle zero values, while Box-Cox also normalizes your data, which the other two do not do.
- For left-skewed data: First reflect the data and then apply the techniques mentioned for right-skewed data.
- To stabilize the variance: Use Box-Cox or Yeo-Johnson (similar to Box-Cox but also handles zero and negative values).
- To center the mean and scale: Use z-score standardization (standard deviation = 1).
- For range-bounded scaling (fixed range, i.e. (2,5)): Use min-max scale.
Let's generate a right-skewed dataset and apply the log transformation to the entire data to see how this works:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate right-skewed data
np.random.seed(42)
data = np.random.exponential(scale=2, size=1000)
df = pd.DataFrame(data, columns=('value'))
# Apply Log Transformation (shifted to avoid log(0))
df('log_value') = np.log1p(df('value'))
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Original Data - Scatter Plot
axes(0, 0).scatter(range(len(df)), df('value'), alpha=0.5)
axes(0, 0).set_title('Original Data (Scatter Plot)')
axes(0, 0).set_xlabel('Index')
axes(0, 0).set_ylabel('Value')
# Original Data - Box Plot
sns.boxplot(x=df('value'), ax=axes(0, 1))
axes(0, 1).set_title('Original Data (Box Plot)')
axes(0, 1).set_xlabel('Value')
# Log Transformed Data - Scatter Plot
axes(1, 0).scatter(range(len(df)), df('log_value'), alpha=0.5)
axes(1, 0).set_title('Log Transformed Data (Scatter Plot)')
axes(1, 0).set_xlabel('Index')
axes(1, 0).set_ylabel('Log(Value)')
# Log Transformed Data - Box Plot
sns.boxplot(x=df('log_value'), ax=axes(1, 1))
axes(1, 1).set_title('Log Transformed Data (Box Plot)')
axes(1, 1).set_xlabel('Log(Value)')
plt.tight_layout()
plt.show()
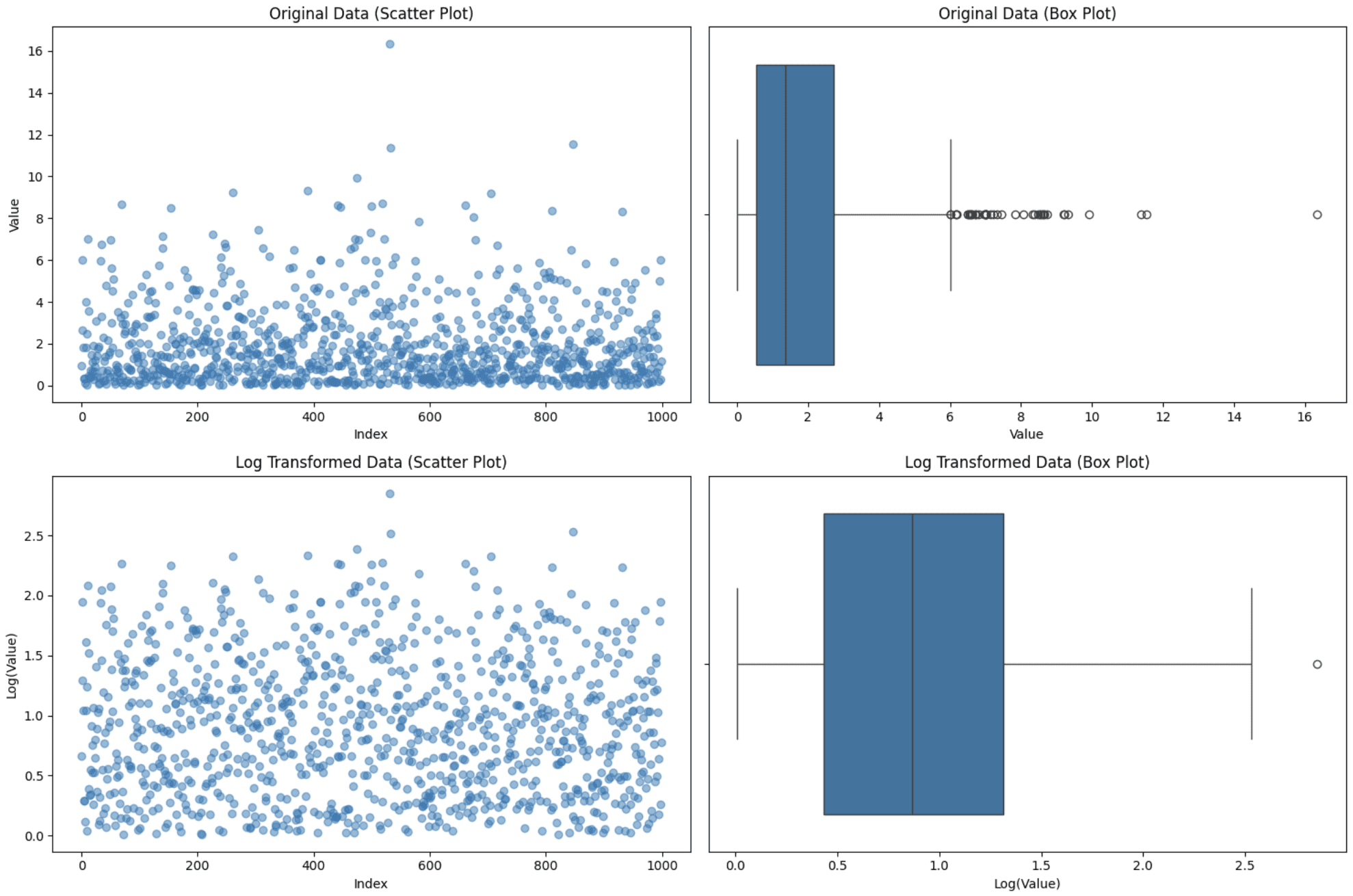

Application of logarithmic transformation
You can see that a simple transformation has handled most of the outliers and reduced them to just one. This demonstrates the power of the transformation to handle outliers. In this case, you need to be cautious and know your data well enough to choose the right transformation, as not doing so can get you into trouble.
Ending up
This brings us to the end of our discussion on outliers, the different ways to detect them, and how to handle them. This article is part of the Pandas series and you can check out other articles on my author page. As mentioned above, here are some additional resources for you to study more about outliers:
- Outlier Detection Methods in Machine Learning
- Different transformations in Machine Learning
- Types of transformations for a better normal distribution
Kanwal Mehreen Kanwal is a machine learning engineer and technical writer with a deep passion for data science and the intersection of ai with medicine. She is the co-author of the eBook “Maximizing Productivity with ChatGPT.” As a Google Generation Scholar 2022 for APAC, she champions diversity and academic excellence. She is also recognized as a Teradata Diversity in tech Scholar, Mitacs Globalink Research Scholar, and Harvard WeCode Scholar. Kanwal is an ardent advocate for change and founded FEMCodes to empower women in STEM fields.






